Целевая функция стремится к экстремуму — максимуму или минимуму. Ограничения задаются в виде системы уравнений. Дополнительно накладываются условия целочисленности значений искомых переменных. [c.435]
Точные методы решения задач целочисленного линейного программирования основаны на временном отказе от требования целочисленное переменных. В этих задачах отбрасывается условие целочисленности переменных и решается обычная задача линейного программирования. После нахождения оптимального плана задачи линейного программирования могут представиться два случая. [c.187]
| Рис. 1.13. Решение задачи (1.1) при условии целочисленности ее переменных |  |
| Рис. 1.14. Ввод условия целочисленности переменных задачи (1.1) |  |
Первая часть курса - "Принятие оптимальных решений в условиях определенности", представленная в настоящей книге, посвящена рассмотрению моделей линейной оптимизации, использованию условий целочисленности в линейных моделях (учету проблемы постоянных издержек и рассмотрению задач типа "брать/не брать"). Важными частными случаями задач линейной оптимизации, рассмотренными в первой части курса, являются транспортная задача и задача о назначениях. [c.18]
В некоторых случаях условие целочисленности переменных имеет принципиальное значение и позволяет исследовать новый класс моделей. В разделе "Использование целочисленных переменных в задачах линейного программирования" мы рассмотрим такие типы моделей. Однако следует иметь в виду, что добавление этого ограничения исключает использование эффективных методов решения задач линейного программирования (которые будут упомянуты в следующих разделах). Задача с целочисленными переменными гораздо более сложна для исследования, а алгоритмы ее решения гораздо менее универсальны и эффективны. [c.46]
Таким образом, если вы хотите использовать наиболее эффективные алгоритмы решения задачи линейного программирования, не задавайте без нужды условие целочисленности. [c.46]
Это особенно важно, когда вы исследуете большую модель (несколько десятков и сотен переменных и ограничений). Впрочем, для простых примеров, рассмотренных в данной главе, использование условия целочисленности переменных не приведет ни к каким осложнениям. Так что можете попробовать... [c.46]
Оптимальный план для кондитерской фабрики (с условием целочисленности переменных) [c.99]
Помимо рассмотренных вполне очевидных случаев, в которых необходимо введение условия целочисленности, существует и другая область использования целочисленных переменных в ЛП-задачах. Весьма часто на практике возникают задачи, когда требуется решить, какие элементы из большого их набора нужно выбрать, чтобы оптимизировать целевую функцию и удовлетворить заданным ограничениям, а какие отбросить. Этот класс задач по-английски называют задачами типа "go/no go", что по-русски соответствует дилемме "брать/не брать". Часто также о подобных задачах говорят как о задачах "загрузки вещевого мешка", имея в виду следующую "туристическую" аналогию. Имеется множество предметов, которые вы хотели бы взять в поход, но все они не входят в вещевой мешок. Вы приписываете каждой вещи определенную величину ценности и пытаетесь заполнить мешок наиболее ценными вещами, удовлетворяя одновременно ограничения по суммарному объему и весу содержимого мешка. [c.100]
Иными словами, мы требуем, чтобы сумма всех переменных в любой строке составляла единицу и сумма всех переменных в любом столбце также была бы равна единице. Ясно, что, поскольку все переменные предполагаются неотрицательными, единственная возможность удовлетворить этим равенствам - это положить одну из переменных в каждой строчке и в каждом столбике равной 1, а все остальные - равными нулю. Никаких дополнительных условий целочисленности не требуется. [c.136]
Интересно повторить решение ЛП-задачи с ограничением на индексы команд, а также решение этой задачи с явным условием целочисленности переменных решения, если потребовать, чтобы индекс каждой команды был не больше 9 (или еще меньше). [c.142]
| Рис. 26. Результаты для примера "Построение команд" при ограничении на индекс команд и условии целочисленности | 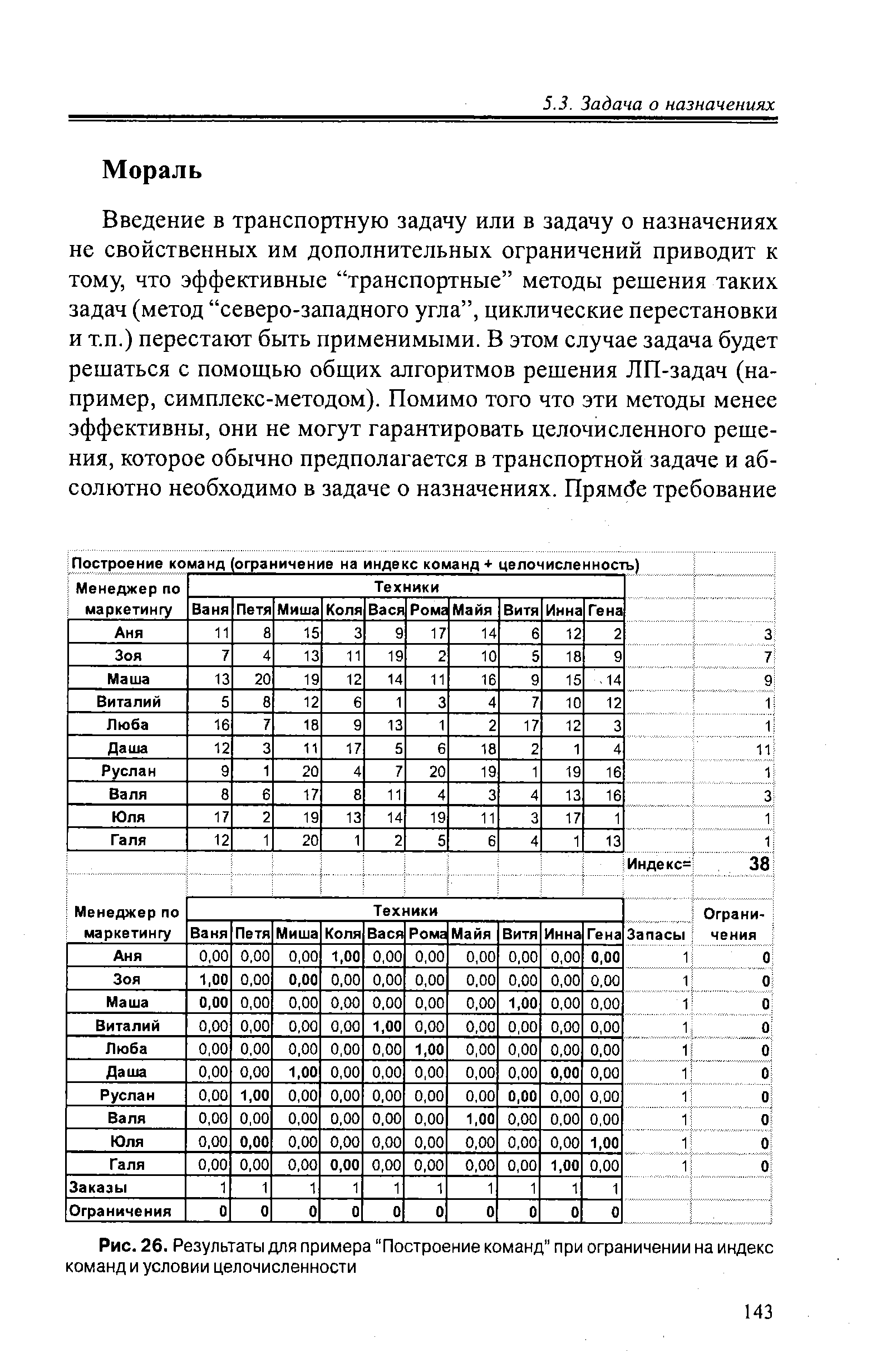 |
Ответ в тексте, в начале раздела 4, пункт "Условие целочисленное ". [c.271]
В этом случае условие целочисленности абсолютно необходимо. Если его снять, получим решение, в котором суммарные обрезки равны 50 футам, а количество распилов разных типов следующее [c.282]
Последнее условие говорит о том, что предметы неделимы (условие целочисленное ). [c.102]
Ячейки с отрицательными числами соответствуют работам-стрелкам, направленным от событий с большими номерами к событиям с меньшими номерами. Для использования процедуры поиска решения с целью упорядочения графика будем полагать заголовки столбцов таблицы изменяемыми ячейками, а требования, чтобы значения всех ячеек с формулами были не менее единицы, — ограничениями задачи. Эти требования соответствуют условиям направленности работ-стрелок от событий с меньшими номерами к событиям с большими номерами. Другими естественными ограничениями служат условия целочисленное и положительности номеров событий, т.е. ячеек [c.303]
Ячейки с отрицательными числами соответствуют работам-стрелкам, направленным от событий с большими номерами к событиям с меньшими номерами. Для использования процедуры поиска решения с целью упорядочения графика будем полагать заголовки столбцов таблицы изменяемыми ячейками, а требования, чтобы значения всех ячеек с формулами были не менее единицы, — ограничениями задачи. Эти требования соответствуют условиям направленности работ-стрелок от событий с меньшими номерами к событиям с большими номерами. Другими естественными ограничениями служат условия целочисленное и положительности номеров событий, т.е. ячеек СЗ — L3. Номера начального и последнего событий остаются без изменений, поэтому все остальные искомые значения номеров событий заключены в интервале между начальным и последним событиями. [c.186]
Сформулированная математическая задача отличается от задачи линейного программирования только последним условием целочисленности. Однако наличие этого условия позволяет (в данном конкретном случае) легко решить задачу перебором. Действительно, как ограничение по стоимости, так и ограничение по площади показывают, что х < 4. Значит, х может принимать лишь одно из пяти значений 0, 1, 2, 3, 4. " > [c.175]
В ряде случаев за переменные величины в модели удобно принимать не объемы, а доли. Тогда значения переменных будут задавать не план производства как таковой, а его структуру. Откажемся в модели (1.33)— 1.37) от условий целочисленности переменных и представим ее как обычную линейную модель. Для этого достаточно заменить в ней ограничения вида (1.37) на ограничения неотрицательности переменных [c.34]
Случай 4. Требование целочисленности решения даже при наличии прочих линейных ограничений и линейной целевой функции ведет к невыполнению условий 1 и 4. Из рис. 2.5 видно, что область допустимых целочисленных значений переменных состоит из четырех точек О, A, D и Е, а оптимум достигается в точке D. Причем это решение не только существенно хуже оптимального решения без условий целочисленности (достигается в точке В), но и не может быть получено путем его округления до ближайших целых чисел (точки А и Q. [c.64]
Вариантные расчеты могут проводиться также при варьировании элементов самой модели изменении критерия оптимальности, добавлении новых ограничений на ресурсы или на способы их использования, расширении множества вариантов, введении в модель условий целочисленного или вероятностного характера, изменении некоторых переменных, решении задачи разными методами и т. д. Эти расчеты во многих случаях осуществляются для повышения обоснованности решения, особенно если оно является весьма важным. Но чаще они применяются для отработки самих моделей, проверки их соответствия реальной действительности. Кроме того, вариантные расчеты используются при отсутствии точных методов поиска оптимального решения модели. [c.123]
Целочисленное программирование ориентировано на решение задач, в которых все или некоторые переменные должны принимать только целые значения. Задача называется полностью целочисленной, если условие целочисленности наложено на все ее переменные когда это условие относится лишь к некоторым переменным, задача называется частично целочисленной. [c.464]
Игнорируя условия целочисленности, получим X =(1/ 2 0 9/2). Никакое округление компонентов этого плана не дает допустимого решения, так как искомое целочисленное решение х (2 2> 5) Таким образом, для решения целочисленных задач необходимы специальные методы. [c.465]
Начальный шаг решения этой задачи состоит в нахождении решения задачи ЛП, получаемой при отбрасывании условия целочисленности х ил/г- Обозначим эту задачу через ЛП-1. На рис. 2.2 представлено графическое решение задачи ЛП-1. [c.473]
Идея такого алгоритма заключается в следующем вначале условие целочисленности не принимается во внимание и симплекс-методом отыскивается оптимальный план. Если этот план нецелочисленный, составляется дополнительное ограничение, которому удовлетворяет любое целочисленное решение, но заведомо не удовлетворяет найденное. [c.386]
Сравнительно легко показать, что всякий оптимальный опорный план задачи линейного программирования, рассматриваемой на множестве R, является также оптимальным опорным планом той же задачи, но рассматриваемой на дискретном множестве R. Исходя из этого утверждения вроде бы можно предложить такой способ решения задачи целочисленного программирования а) определить множество R целых точек многоугольника ограничений Q б) образовать его линейную выпуклую оболочку R в) на множестве R решить задачу линейного программирования без условия целочисленности. Полученное решение и будет являться решением поставленной задачи. [c.111]
В результате произведенных исследований установлено, что даже при прочих равных условиях целочисленные оптимальные планы отличаются друг от друга различным составом емкостей как по типу, так и по размеру в зависимости от величины ре-зервуарного парка нефтебазы и его пропускной способности. Иными словами, эффективность применения одних и тех же резервуаров неодинакова для различных по объему нефтехранилищ и ограничивается конкретными условиями эксплуатации нефтебазы, которые учитываются в разработанном алгоритме оптимизации. [c.150]
Кроме того, отказ от обычной ЛП-модели в пользу ЛП-модели с требованием целочисленности переменных делает невозможным получение информации об устойчивости решения и о теневых ценах. Поэтому "Поиск решения" MS-Ex el не формирует отчета об устойчивости, если в качестве одного из ограничений введено условие целочисленности хотя бы для одной переменной. Это лишает аналитика и менеджера важного инструмента анализа оптимального решения и определения путей его улучшения через изменение параметров модели. [c.99]
Для однозначного решения задачи необходимо потребовать, чтобы каждый номер события встречался один раз. С этой Целью используем в рабочем листе Ex el для подсчета количества одинаковых номеров событий и последующего введения соответствующих ограничений функции ОКРУГЛ и СЧЁТЕСЛИ, как показано на рис. 4,13. Проведенные расчеты с помощью процедуры поиска решения. показали, что целесообразно отказаться вначале от требования условия целочисленное (как и во многих других задачах, это является серьезным затруднением для указанной процедуры) и воспользоваться затем округлением до целых значений. [c.186]
В последние годы получил развитие и другой путь обоснования оптимального числа гнезд в прессовых и литьевых формах — в не разрывной связи с оптимизацией загрузки технологического оборудования. Как известно, специфической чертой производства изделий из пластмасс является стремление использовать формы с одинаковым числом гнезд. В заводской практике очень редки случаи, когда в распоряжении цеха имеются одновременно формы с различным числом гнезд для изготовления одного и того же изделия. В связи с этим в экономико-математической модели должно быть учтено требование изготовления каждого изделия в формах с одинаковой гнездностью, что существенно изменяет математическую модель загрузки оборудования по сравнению с другими отраслями. Это требование выражается условием целочисленности переменных [c.211]
Заменим решение исходной целочисленной задачи линейного программирования на многоугольнике решением ряда задач линейного программирования на многоугольниках ( , ( 2, Qa,... Здесь ( = Q. Многоугольники эти таковы, что множество целых точек в них одно и то же. Таким образом, понятно, что если оптимальный план задачи линейного программирования на многоугольнике Qs удовлетворяет условию целочисленности, то он является и оптимальным целочисленным планом исходной задачи. Процесс решения на этом заканчивается. Если же на многоугольнике Qs оптимальный план не удовлетворяет условию целочисленности, то происходит переход к < а+1 путем добавления одного правильного отсечения (на рис. 15 прямая АВ). Это вновь добавленное неравенство гарантирует, что оптимальный план, в котором не выполнялось условие целочисленности, заведомо не будет даже допустимым планом в последующих задачах. Ну, а множества целых точек это неравенство не сужает. Иными словами, правильные отсечения позволяют выбрасывать заведомо ненужные точки многоугольника ограничений, не теряя при этом нужных точек. Такая идея и лежит в основе метода Гомори. Ему удалось предложить алгориф-мический процесс построения правильных отсечений, не использующий ни рисунка, ни каких-либо других интуитивных соображений, что сделало бы его непригодным для решения многомерных задач. Кратко опишем этот алгорифм. [c.112]
Смотреть страницы где упоминается термин Условие целочисленности
: [c.114] [c.132] [c.148] [c.258] [c.17] [c.7] [c.98] [c.142] [c.298] [c.299] [c.88] [c.493] [c.304] [c.189]Смотреть главы в:
Методы оптимизации управления для менеджеров -> Условие целочисленности
