К математическим средствам оценки рисков относятся статистические расчеты, нормальное распределение, логарифмически нормальное распределение, линейное программирование, эконометрические методы и т.д. [c.734]
Распределение инвариантное 222 Распределение Коши 236, 241, 243 Распределение Леви-Смирнова 241 Распределение логарифмически [c.485]
Логарифмический метод. Этот метод дает логарифмически пропорциональное распределение прироста показателя по анализируемым факторам. Для факторной системы z=xy абсолютное изменение показателя z за счет факторов х и у определяется по формулам [c.275]
Логарифмический метод. Этот метод, описанный В. Федоровой и Ю. Егоровым [66, с. 71 — 73], состоит в том, что достигается логарифмически пропорциональное распределение остатка по двум искомым факторам. В этом случае не требуется установления очередности действия факторов. [c.124]
Пропорциональное распределение остатка по факторам достигается с помощью логарифмического метода. [c.39]
Интегральный способ. Этот способ позволяет избежать недостатков, присущих методу цепной подстановки, и не требует применения приемов по распределению неразложимого остатка по факторам, так как в нем действует логарифмический закон перераспределения факторных нагрузок. [c.46]
Непрерывная случайная величина X имеет логарифмически нормальное (сокращенно — логнормальное распределение), если ее логарифм подчинен нормальному закону. [c.35]
На левой гистограмме мы делаем предположение, что для предприятия г-жи Хартии Вольнэсти возможны только два исхода - высокий спрос или низкий спрос. На гистограмме показана приведенная стоимость в первом году при допущении, что бизнес не останавливается. Логарифмическое нормальное распределение на правом рисунке более реалистично, поскольку подразумевает бесконечный ряд возможных значений приведенной стоимости и учитывает промежуточные результаты Модель Блэка—Шольца основана на логарифмическом распределении. [c.567]
Гипотеза о логарифмически нормальном распределении коэффициентов элементарного перехода обеспечивает удобство и простоту про- [c.158]
| Рис. 4.2.3. Вид плотности распределения для суммы логарифмически нормально распределенных случайных величин | 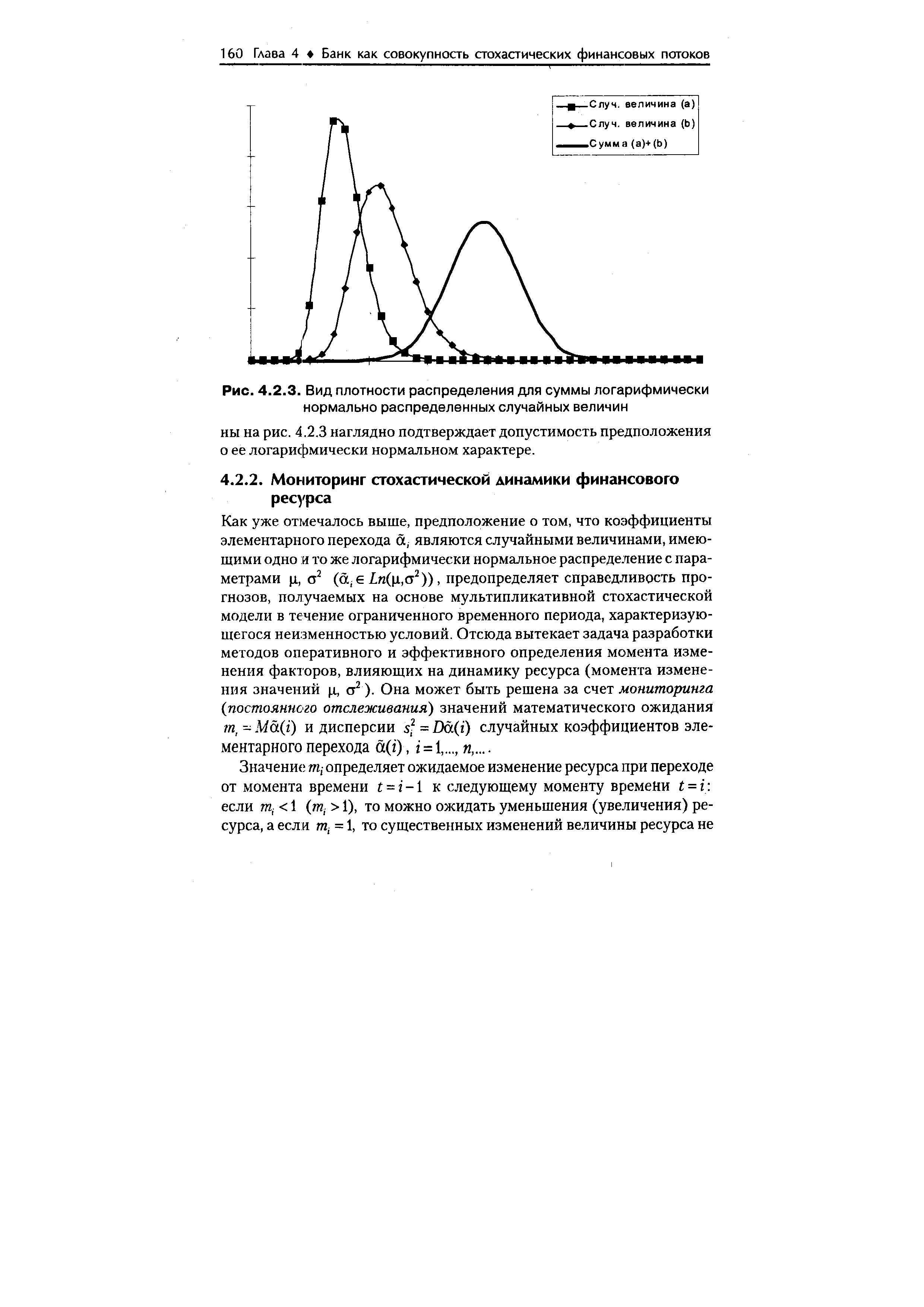 |
Предположим, что случайная величина а имеет логарифмически нормальное распределение (ае 1и( ха,а2)) с математическим ожиданием ц и с дисперсией а2, то есть предположим, что логарифм этой случайной величины имеет нормальное распределение с математическим ожиданием ц и с дисперсией a2 ( In a e N( i, сг2)). Плотность распределения [c.182]
Логарифмически-нормальное распределение. Распределение случайной величины Y называется логарифмически-нормальным, если логарифм этой величины распределяется по нормальному закону [46] [c.26]
Логарифмически нормальному закону могут подчиняться время простоя некоторых видов оборудования, распределение потребности народного хозяйства в различных типоразмерах, распределение усталостной долговечности, когда предполагается, что логарифм числа циклов нагрузки до разрушения образца распределен по нормальному закону. [c.27]
Принято логарифмическое распределение запасов, позволяющее рассчитать основные экономические показатели освоения ресурсов в этом районе (табл. 16). [c.163]
Дисперсия распределения размеров месторождений моделируется на основе анализа временных серий. Распределение размера запасов открытий обычно принимается логнормальным. Проверка производится на имеющейся статистике. Следует отметить, что дисперсия логнормального распределения не уменьшается с уменьшением средних размеров открытий, поэтому важно прогнозировать распределение открытий по размерам, а не просто средние значения прироста запасов. При гипотезе о лог-нормальном распределении удобно наносить данные о запасах на логарифмический бланк. Из него непосредственно получают вероятности открытий месторождений различной крупности. [c.180]
Для величины потенциальных ресурсов можно указать математическое ожидание и доверительный интервал, который на логарифмической шкале задает интервал 6 а нормального закона распределения. Указанным приемом рассчитывались параметры логнормального закона распределения потенциальных ресурсов НГО I— IV (табл. 22). [c.204]
Добавив на логарифмическую шкалу несколько лет движения цены, вы можете устранить тренды и выделить только Сезонную Тенденцию каждого товара или акции. Данную Сезонную Тенденцию можно применять вместе с анализом Волны Эллиота, что поможет с распределением во времени различных составляющих Расчётов по Волне. [c.67]
Логарифмически нормальное распределение [c.99]
| Рисунок 3-15 Нормальное и логарифмически нормальное распределения | 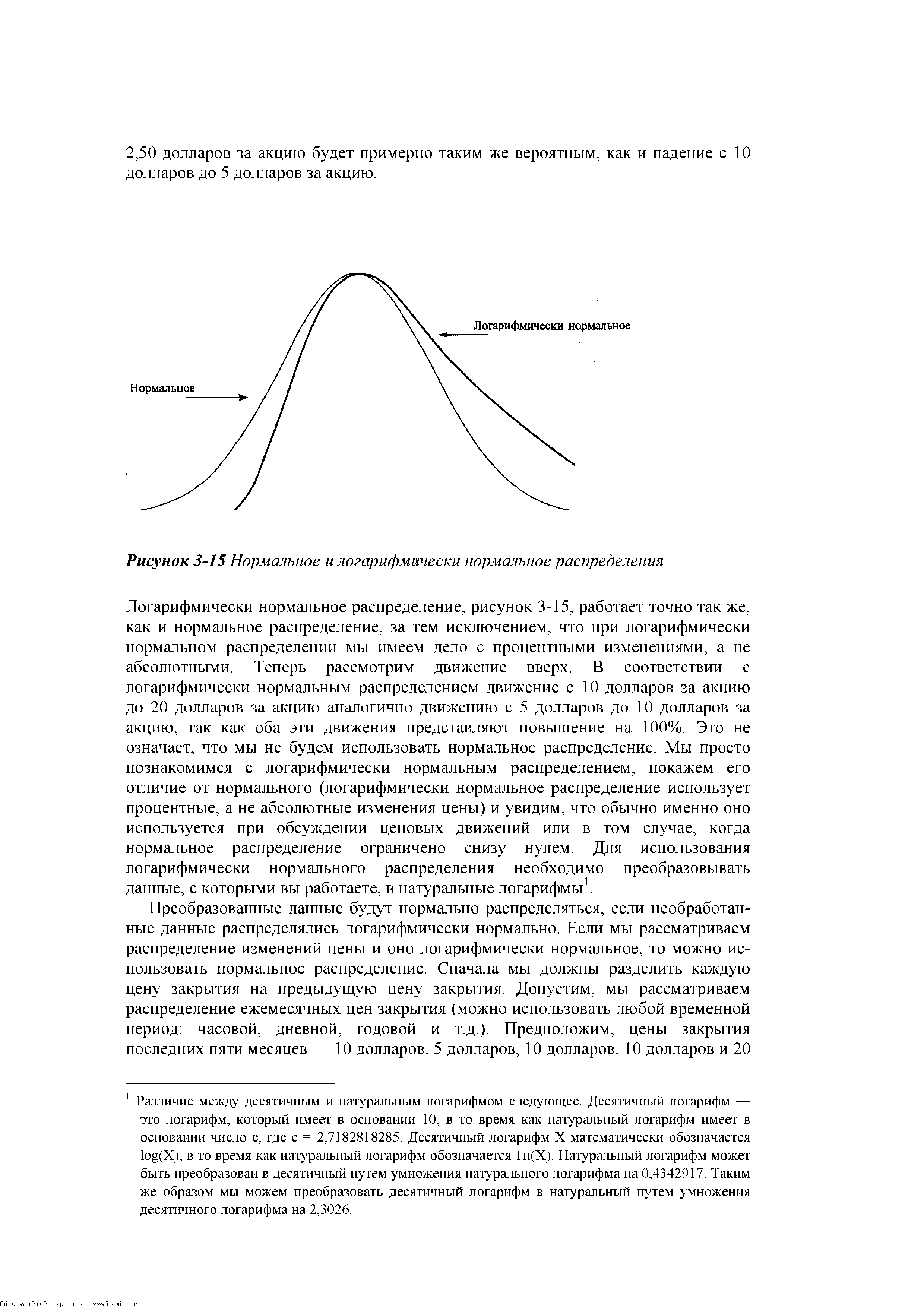 |
Тот факт, что распределение изменений волатильности логарифмически нормально, не так часто принимается во внимание. Чрезвычайная чувствительность цен опционов к волатильности базового инструмента делает покупку опциона (пут-опциона или колл-опциона) еще более привлекательной в смысле математического ожидания. [c.160]
Необходимо отметить, что форма распределения, используемого для Р(Т, U), не обязательно должна быть такой же, как и в модели ценообразования, применяемой для определения значений Z(T, U - Y). Например, вы используете модель фондовых опционов Блэка-Шоулса для определения значений Z(T, U - Y). Эта модель предполагает логарифмически нормальное распределение изменений цены, однако для определения соответствующего Р(Т, U) вы можете использовать другую форму распределения. [c.168]
| Рис. 22. Функция распределения вероятности квадрата скорости жидкости, нормализованная к ее среднему времени, в одиннадцатом слое игровой модели гидродинамической турбулентности, обсуждаемой в тексте. Вертикальная ось имеет такой логарифмический масштаб, что прямая линия, которая помогает глазу, квалифицируется, как очевидное показательное распределение. Обратите внимание на появление чрезвычайно редких и больших взрывов скоростей на краю, выше экстраполяции прямой линии. Источник [252]. | ![Рис. 22. <a href="/info/21981">Функция распределения вероятности</a> квадрата скорости жидкости, нормализованная к ее среднему времени, в одиннадцатом слое игровой модели гидродинамической турбулентности, обсуждаемой в тексте. Вертикальная ось имеет такой логарифмический масштаб, что прямая линия, которая помогает глазу, квалифицируется, как очевидное <a href="/info/5302">показательное распределение</a>. Обратите внимание на появление чрезвычайно редких и больших взрывов скоростей на краю, выше экстраполяции прямой линии. Источник [252].](/pic1/205196012179108108119160056012034002236089221065.png) |
| Рис. 23. Функция распределения вероятности квадрата скорости как на Рис. 22, но для гораздо более длинного ряда времени, чтобы хвост распределений для очень больших флуктуации был намного лучше ограничен. Гипотеза о том, что не существует "выбросов" здесь проверяется "разрушением" распределения для трех показанных слоев. В то время, как это имеет успех для маленьких колебаний, хвосты распределений для больших событий весьма различны, указывая, что экстремальные колебания принадлежат к собственному классу и, следовательно, "выбросы". Вертикальная ось снова в логарифмическом масштабе. Источник [252]. | ![Рис. 23. <a href="/info/21981">Функция распределения вероятности</a> квадрата скорости как на Рис. 22, но для гораздо более длинного <a href="/info/4684">ряда времени</a>, чтобы хвост распределений для очень больших флуктуации был намного лучше ограничен. Гипотеза о том, что не существует "выбросов" здесь проверяется "разрушением" распределения для трех показанных слоев. В то время, как это имеет успех для маленьких колебаний, хвосты распределений для больших событий весьма различны, указывая, что экстремальные колебания принадлежат к собственному классу и, следовательно, "выбросы". Вертикальная ось снова в логарифмическом масштабе. Источник [252].](/pic1/151255070046029077102042074146191012187176133187.png) |
VAR-таянз осуществляется разными методами, наиболее известный из них — дельта-нормальный метод, в основе которого лежит предположение о нормальном законе распределения логарифмических доходностей рыночных инструментов. Основные достоинства дельта-нормального метода относительная простота реализации, сравнительно небольшие затраты, приемлемая точность оценки. Как метод статистической оцен- [c.598]
Дельта-нормальный (delta-normaO метод расчета величины VaR позволя ет получить оценку VaR в замкнутом виде. В его основе лежит посылка о нор мальном законе распределения логарифмических доходностей факторе] рыночного риска (цен первичных неразложимых активов, от которых зависи стоимость более сложных инструментов, позиций и портфеля в целом) [c.251]
В ряде исследований утверждается, что для отказов технических изделий вследствие износа, усталости, коррозии и старения вполне удовлетворительным будет нормальный или логарифмически нормальный закон распределения, в случае же внезапных отказов, возникающих вследствие случ-айных перегрузок, аварий и т. д., подходит экспоненциальный закон распределения [14]. [c.62]
Выражение (4) для Az представляет собой не что иное, как его логарифмическое пропорциональное распределение по двум искомым факторам. Именно поэтому авторы такого подхода назвали этот метод логарифмическим методом разложения приращения Az на факторы . Особенность логарифмического метода разложения состоит в том, что он позволяет определить безостаточное влияние не только двух, но и многих изолированных факторов на изменение результативного показателя, не требуя установления очередности действия. [c.125]
Длительное продолжение добычи даже в условиях спада вполне возможно и повсеместно практикуется. Однако логарифмически нормальная кривая распределения Хабберта на практике замещается фрактальным распределением7. На поздних стадиях добычу можно продлить за счет разработки большого числа тех менее крупных месторождений и геологических структур, которые часто пропускают или не принимают в расчет при первичном, широкомасштабном исследовании продуктивной провинции. [c.58]
С помощью этой модификации нормальное распределение преобразуется в логарифмически нормальное распределение. Цена любого свободно котируемого инструмента имеет нулевое значение в качестве нижнего предела1. Поэтому когда цена этого инструмента падает и приближается к нулю, то, теоретически, цене инструмента должно быть все труднее понизиться. Рассмотрим некую акцию стоимостью 10 долларов. Если бы акция упала на 5 долларов до 5 долларов за акцию (50% понижение), то в соответствии с нормальным распределением она может также легко упасть с 5 долларов до 0 долларов. Однако при логарифмически нормальном распределении подобное падение на 50% с цены в 5 долларов за акцию до цены [c.100]
Логарифмически нормальное распределение, рисунок 3-15, работает точно так же, как и нормальное распределение, за тем исключением, что при логарифмически нормальном распределении мы имеем дело с процентными изменениями, а не абсолютными. Теперь рассмотрим движение вверх. В соответствии с логарифмически нормальным распределением движение с 10 долларов за акцию до 20 долларов за акцию аналогично движению с 5 долларов до 10 долларов за акцию, так как оба эти движения представляют повышение на 100%. Это не означает, что мы не будем использовать нормальное распределение. Мы просто познакомимся с логарифмически нормальным распределением, покажем его отличие от нормального (логарифмически нормальное распределение использует процентные, а не абсолютные изменения цены) и увидим, что обычно именно оно используется при обсуждении ценовых движений или в том случае, когда нормальное распределение ограничено снизу нулем. Для использования логарифмически нормального распределения необходимо преобразовывать данные, с которыми вы работаете, в натуральные логарифмы1. [c.101]
Мы немного познакомились с математикой нормального и логарифмически нормального распределения и теперь посмотрим, как находить оптимальное f по нормально распределенным результатам. Формула Келли является примером параметрического оптимального f, где f является функцией двух параметров. В формуле Келли вводные параметры — это процент выигрышных ставок и отношение выигрыша к проигрышу. Однако формула Келли даст вам оптимальное f только тогда, когда возможные результаты имеют бернуллиево распределение. Другими словами, формула Келли даст правильное оптимальное f, когда есть только два возможных результата, в противном случае, как, например, в нормально распределенных результатах, формула Келли не даст вам правильное оптимальное f2. [c.102]
Таким образом, в соответствии с моделью Блэка для фьючерсов справедливая стоимость колл-опциона с ценой исполнения 600, сроком исполнения 15 сентября 1991 года, при цене базового инструмента на 1 августа 1991 года 575, при вола-тильности 25%, с учетом 252-дневного года и R = 0 составляет 10,1202625. Интересно отметить связь между опционами и базовыми инструментами, используя вышеперечисленные модели ценообразования. Мы знаем, что 0 является наименьшей ценой опциона, но верхняя цена — это цена самого базового инструмента. Модели демонстрируют, что теоретическая справедливая цена опциона приближается к верхнему значению (стоимости базового инструмента U) при росте любой или всех трех переменных Т, R или V Это означает, что если мы, например, увеличим Т (время до срока истечения опциона) до бесконечно большого значения, тогда цена опциона будет равна цене базового инструмента. В этой связи мы можем сказать, что все базовые инструменты в действительности эквивалентны опционам с бесконечным Т. Таким образом, все сказанное верно не только для опционов, но и для базовых инструментов, как будто они являются опционами с бесконечным Т. Модель фондовых опционов Блэка-Шоулса и модель опционов на фьючерсы Блэка построены на определенных допущениях. Разработчики этих моделей исходили из трех утверждений. Несмотря на недостатки этих утверждений, предложенные модели все-таки довольно точны, и цены опционов будут стремиться к значениям, полученным из моделей. Первое из этих утверждений состоит в том, что опцион не может быть исполнен до истечения срока. Это приводит к недооценке опционов алгериканского типа, которые могут исполняться до истечения срока. Второе утверждение предполагает, что мы знаем будущую волатильность базового инструмента, и она будет оставаться постоянной в течение срока действия опциона. На самом деле это не так (т.е. волатильность изменится). Кроме того, распределение изменений волатильности логарифмически нормально, и эту проблему модели не учитывают1. Еще одно допущение модели состоит в том, что безрисковая процентная ставка остается постоянной в течение времени действия опциона. Это также не обязательно. Более того, краткосрочные ставки логарифмически нормально распределены. То обстоятельство, что, чем выше краткосрочные ставки, тем выше будут цены опционов, и утверждение относительно неизменности краткосрочных ставок может привести к еще большей недооценке опциона по отношению к ожидаемой цене (его правильному арифметическому математическому ожиданию). Еще одно утверждение (возможно наиболее важное), которое может привести к недооценке стоимости опциона, рассчитанной с помощью модели, по отношению к действительно ожидаемой стоимости, состоит в том, что логарифмы изменений цены распределяются нормально. Если бы опционы характеризовались не числом дней до даты истечения срока, а числом тиков вверх или вниз до истечения, а цена за один раз могла бы изменяться только на 1 тик и он был бы статистически независим от предыдущего тика, то мы могли бы допустить существование нормального распределения. В нашем случае логарифмы изменений цены не имеют таких характеристик. Тем не менее теоретические справедливые цены, полученные с помощью моделей, используются профессионалами на рынке. Даже если некоторые трейдеры применяют модели, которые отличаются от показанных здесь, большинство из них дадут похожие теоретические справедливые цены. Когда реальные цены расходятся с теоретическими до такой степени, что спекулянты могут получить прибыль, цены начинают снова сходиться к так называемой теоретической справедливой цене . Тот факт, что мы можем спрог-нозировать с [c.160]
Поскольку, в случайной модели без памяти, существует больше половины просадок с продолжительностью большей, чем один временной период, то удобно визуализировать эмпирическое распределение этих просадок на рынке акций в логарифмическом масштабе, где ожидаемое показательное распределение становится прямой линией. Это весьма эффективный метод проверить действительность гипотезы отклонения от прямой линии будут сигнализировать некоторое отклонение от показательного распределения и, таким образом, от гипотезы об отсутствии памяти. [c.67]
| Рис. 27. Две пунктирных линии определены так, чтобы 99% просадок синтетического ряда GAR H (1,1) с шумовым распределением Стьюдента с 4 степенями свободы оказываются в пределах этих двух линий. Символы+представляют совокупное распределение просадок для DJIA. Ордината находится в логарифмическом масштабе, в то время как абсцисса показывает просадку например, -0.30 соответствует спаду -30 %. Источник [399]. | ![Рис. 27. Две пунктирных линии определены так, чтобы 99% просадок синтетического ряда GAR H (1,1) с шумовым <a href="/info/5304">распределением Стьюдента</a> с 4 <a href="/info/21621">степенями свободы</a> оказываются в пределах этих двух линий. Символы+представляют совокупное распределение просадок для DJIA. Ордината находится в логарифмическом масштабе, в то время как абсцисса показывает просадку например, -0.30 соответствует спаду -30 %. Источник [399].](/pic1/033084192106253035035144060088180025153175163011.png) |
Смотреть страницы где упоминается термин Распределение логарифмически
: [c.163] [c.588] [c.126] [c.301] [c.154] [c.166] [c.200] [c.331] [c.163] [c.27]Основы стохастической финансовой математики Т.2 (1998) -- [ c.0 ]
