| Таблица 5. Дики Фуллер тест для единичных корней, показывающий | 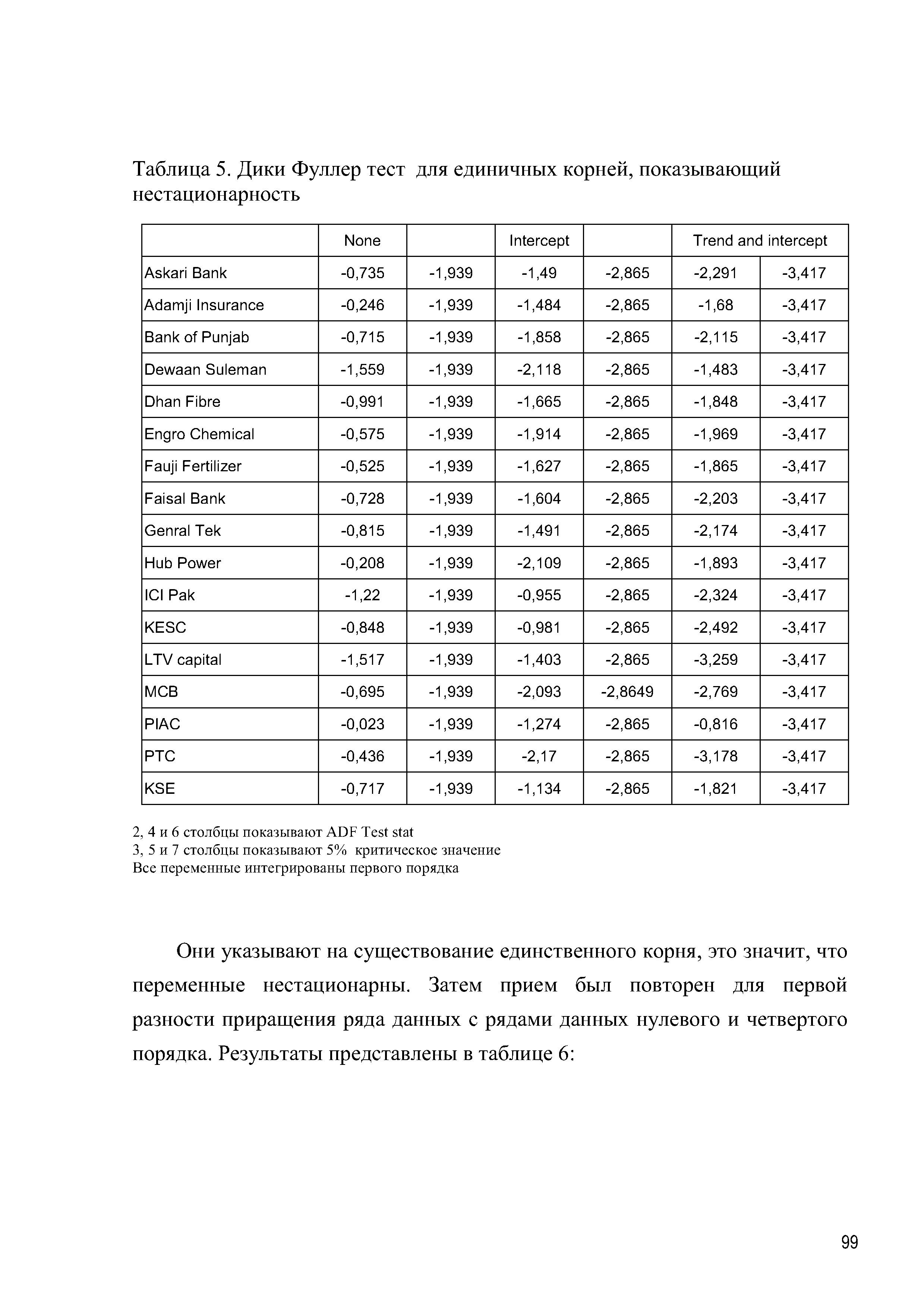 |
| Таблица 6. Дики Фуллер тест для единичных корней, | 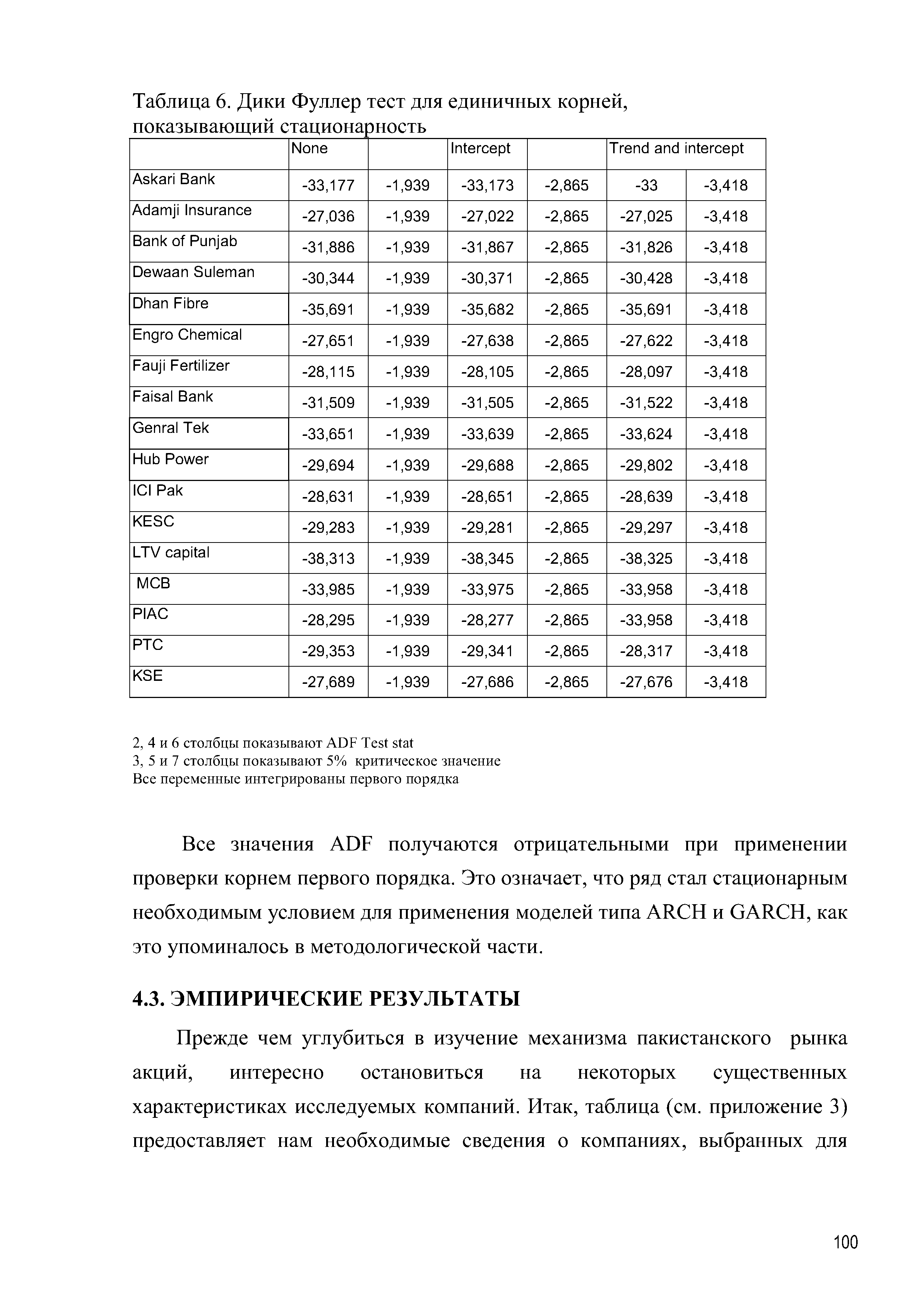 |
Дики-Фуллера, 280 Статистический тест, 539 Стационарность, 276 [c.574]
Однако оказывается, что тест Дики—Фуллера в этом случае неприменим При его использовании гипотеза о нестационарности комбинации будет отвергаться слишком часто. На самом деле критические значения для /-статистики в этом случае другие. Они были оценены методом симуляции (методом Монте-Карло, см. гл. 12). Сравнение наблюдаемого значения Г-статистики с этими уточненными оценками критических зна- [c.221]
Если порядок процесса AR(p) заранее неизвестен, то рекомендуется включать возможно большее количество лагов, чтобы устранить возможную автокорреляцию ошибок. Дело в том, что в ADF тесте предполагается, что ошибки являются белым шумом и критические значения, указанные в таблице 11.1, справедливы только при этом условии. Однако включение чрезмерного количества лагов снижает мощность теста. Чтобы определить количество лагов, которое надо включить в уравнение, можно использовать критерии выбора порядка ARMA модели, описанные ниже, или статистическую значимость дополнительной лаговой переменной. Заметим, что тест Дики-Фуллера включен во все современные эконометрйческие пакеты. [c.281]
Третье — можно использовать формальные тесты на наличие единичного корня (тест Дики-Фуллера DF, расширенный тест Дики-Фуллера ADF, тест МакКинли) и др., часть из которых рассмотрена выше в разделе 11.3. [c.293]
Распределение /-статистики в этом случае описано Дики и Фуллером. Ими же получены критические значения для отвержения гипотезы о нестационарности ряда. Они существенно отличаются от критических значений распределения Стьюдента. В результате оказывается, что использование обычного /-теста приводит к тому, что гипотеза о нестационарности временного ряда отвергается слишком часто, в том числе и тогда, когда ряд действительно является нестационарным. [c.220]
