В настоящем параграфе мы рассмотрим некоторые вопросы, связанные с нестационарными временными рядами. При этом мы не будем ставить задачу обстоятельного изложения теории нестационарных рядов, так как это потребовало бы использования математического аппарата, существенно выходящего за рамки нашего рассмотрения. Поэтому мы ограничимся лишь тем, что затронем основные проблемы, возникающие при эконометрическом моделировании нестационарных временных рядов. [c.218]
Подробнее вопросы, связанные с нестационарными временными рядами, изложены в [1], [13]. [c.222]
Нестационарные временные ряды 218, [c.302]
| Рис. 10.5. Выдача с ЭВМ программы по обработке нестационарного временного ряда уровня продаж (рис. 10.6) с изменяющимся средним по методу кумулятивных сумм | 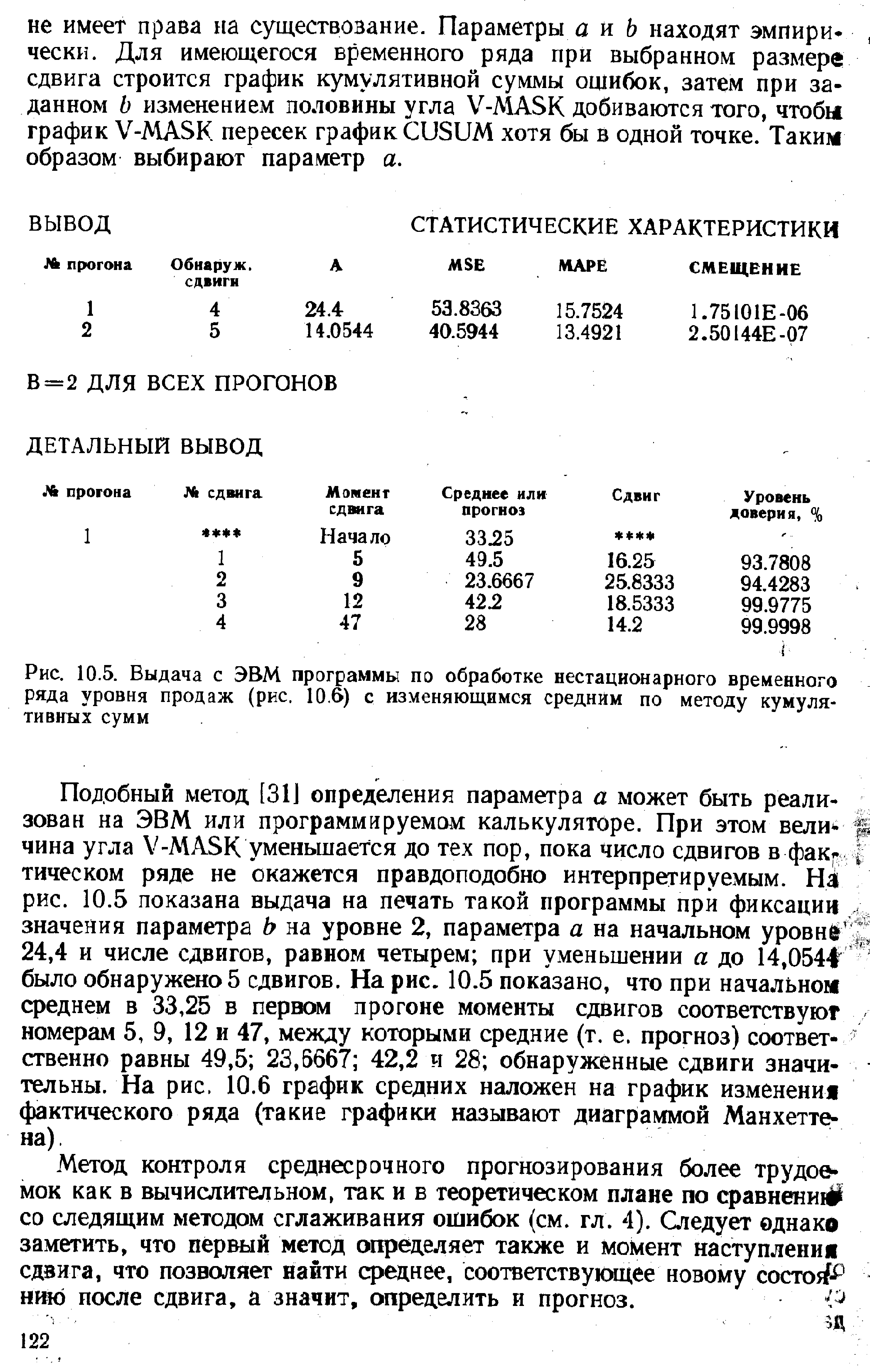 |
Рассмотрим различные примеры нестационарных временных рядов. [c.285]
Типичные примеры графиков нестационарных временных рядов приведены на рисунках 11.1-11.4. [c.286]
Случайное блуждание (11.43) является примером нестационарного временного ряда. Однако, если к нему применить операцию взятия последовательной разности, получим стационарный временной ряд [c.288]
На рисунках 11.5-11.8 приведены автокорреляционные и частные автокорреляционные функции нестационарных временных рядов, представленных на рисунках 11.1-11.4. [c.290]
Прогноз нестационарного временного ряда несколько отличается от выше разобранного случая. Рассмотрим временной ряд yt, первые разности которого zt являются AR(1) процессом (см. (11.67)) [c.309]
Мы видим, что в случае нестационарного временного ряда дисперсия ошибки прогноза монотонно растет с ростом горизонта прогноза s. [c.309]
Разложение временного ряда на компоненты. Стационарные и нестационарные ряды. Автокорреляционная функция. Типы и виды трендов. Полиномиальный тренд. Экспоненциальный и гармонический тренды. Логистическая кривая. Фильтрация тренда. Скользящие средние. Экспоненциальное сглаживание. Метод последовательных разностей. Сплайны. [c.85]
Рассмотренные ситуации не охватывают, однако, наиболее интересных для нас моделей стационарных и нестационарных временных рядов. Мы перейдем теперь к обсуждению основных понятий и фактов, касающихся стационарных и нестационарных временных рядов, и рассмотрению процедур регрессионного анализа временных рядов. [c.12]
В главе 1 мы уже отмечали, что рассмотренные там случаи, в которых можно использовать стандартные процедуры регрессионного анализа несмотря на то, что объясняющие переменные являются стохастическими (ситуации А, А, В, С), не охватывают наиболее интересных для нас моделей стационарных и нестационарных временных рядов. Это замечание относится и к широко используемым на практике моделям авторегрессии, в том числе и стационарным. [c.57]
Модели такого вида будут очень часто встречаться у нас при рассмотрении связей между нестационарными временными рядами. В этих случаях такая модель описывает механизм поддержания долговременной связи [c.76]
Глава 5. Нестационарные временные ряды [c.93]
Начиная с этого раздела, мы обращаемся к методам анализа панельных данных, предназначенным в основном для анализа данных yit, xit i = , ...,N, t = , ...,T , в которых количество субъектов исследования N велико, а количество наблюдений Т над каждым субъектом мало. Вследствие малости Т в таких ситуациях затруднительно использовать технику, интерпретирующую Уи,У-и,---,Ут как, /V временных рядов длины Т (например, технику векторных авторегрессий и моделей коррекции ошибок для нестационарных временных рядов). Основная направленность методов, предполагающих малость Т, - получение по возможности наиболее эффективных оценок коэффициентов. [c.242]
Модели нестационарных временных рядов и их идентификация [c.46]
В чем состоят основные отличия стационарных временных рядов от нестационарных [c.51]
Под стационарным понимается ряд, индивидуальные значения которого, меняясь со временем, не изменяют среднего на достаточно продолжительном отрезке времени. Другими словами, среднее значение спроса за рассматриваемый период не увеличивается и не уменьшается. Нестационарным является ряд, когда среднее не остается постоянным, а изменяется со временем. Изменяющееся среднее называют трендом. [c.121]
Такие параметры социально-экономических объектов, как скорости потоков и накоплений ресурсов, время запаздывания в принятии решений, последовательность (во времени) выделения ресурсов, интервал времени прогнозирования, интервалы времени отвыкания или привыкания к чему-либо, продолжительность времени терпения чего-то и ряд других параметров, являясь функциями времени, во многом определяют характер социально-экономических процессов. Чтобы избежать серьезных ошибок при принятии решений в управлении реальной экономикой, необходимо научиться понимать влияние фактора времени на общественные процессы. Поскольку время течет непрерывно и бесконечно, а общественные системы (экономические, политические, социальные и др.) также непрерывно изменяют свою структуру (что позволяет их считать нестационарными), не может существовать стабильных алгоритмов и незыблемых рекомендаций в управлении экономикой. Так, например, профессионал-шофер, помимо знаний правил вождения, должен уметь управлять автомобилем в постоянно возникающих сложных ситуациях, чтобы доехать до цели. Таким же образом профессионал-экономист, помимо знания академических экономических правил и понимания экономической сущности, должен обладать умением управлять в непредсказуемо изменяющейся обстановке при различных условиях существования объекта управления. [c.8]
Практика показывает, что чаще всего в эконометрических исследованиях нестационарность рассматриваемого временного ряда носит именно характер случайного блуждания. Таким образом, вопрос о нестационарности ряда yt, как правило, сводится к следующему верно ли> что в регрессии у, = py, i + Е,, истинное [c.219]
Распределение /-статистики в этом случае описано Дики и Фуллером. Ими же получены критические значения для отвержения гипотезы о нестационарности ряда. Они существенно отличаются от критических значений распределения Стьюдента. В результате оказывается, что использование обычного /-теста приводит к тому, что гипотеза о нестационарности временного ряда отвергается слишком часто, в том числе и тогда, когда ряд действительно является нестационарным. [c.220]
И модели AR, и модели ARMA могут быть включены в более общий класс процессов. Авторегрессионные интегрированные модели скользящего среднего (ARIMA) специально используются для временных рядов, которые являются нестационарным - эти процессы обладают основной тенденцией в их среднем значении и дисперсии. Однако при использовании последовательных разностей данных результат является стационарным. [c.86]
Клайв Грэнджер показал, что статистические методы, применяемые для стационарных рядов, могут дать неверные результаты при их применении к нестационарным рядам. Он открыл, что определенные комбинации нестационарных временных рядов могут обладать стационарностью, что позволяет корректировать статистические [c.144]
Как мы видели выше, статистические свойства стационарных и нестационарных временных рядов существенно отличаются, и для их моделирования должны применяться различные методы. В данном разделе мы в основном рассмотрим частный случай модели Бокса-Дженкинса, ARMA модели для стационарных временных рядов. Почему большое внимание уделяется именно моделям стационарных временных рядов Дело в том, что многие временные ряды могут быть приведены к стационарному ряду после операций выделения тренда, сезонной компоненты или взятия разности. [c.285]
Коррелограмма стационарного временного ряда быстро убывает с ростом k после нескольких первых значений. Если же график убывает достаточно медленно, то есть основания предположить нестационарность ряда. Кроме A F, можно также построить график частной автокорреляционной функции, PA F, которая также должна быстро убывать для стационарного процесса. [c.290]
Проверка равенства цен (или уровней цен) — обычная задача в исследованиях закона единой цены и паритета покупательной способности. Используя какое-либо (обычно линейное) коинтеграци-онное соотношение, устанавливается стационарность или нестационарность временного ряда относительных цен. Однако, давая ответ типа "всё или ничего", этот традиционный подход не в со- [c.11]
В последующем изложении мы рассмотрим вопросы, связанные с методами различения стационарных (стационарных относительно детерминированного тренда) и нестационарных рядов в рамках ARMA моделей, а также вопросы построения моделей связи между временными рядами. [c.98]
При этом обычно сначала рассматривался сам временной ряд, и проводилась проверка его на нестационарность с использованием критериев Дики - Фуллера. Если гипотеза единичного корня не отвергалась, то после этого переходили к рассмотрению ряда разностей и проверяли гипотезу единичного корня для этого ряда, применяя к ряду разностей процедуру Дики - Фуллера. [c.153]
Эта модель предложена Дж. Боксом и Г. Дженкинсом [15]. Она предназначена для описания нестационарных временных рядов х,, обладающих следующими свойствами [c.46]
Метод ОЛИМП является распространением моделей авторегрессии скользящего среднего для моделирования нестационарных временных рядов. Соотношения модели ОЛИМП соответствуют модели АРСС (р, q), за исключением того что на вход поступает не только стационарные, но и нестационарные ряды, заданы начальные условия для остатков, отсутствуют ограничения на корбни характеристического уравнения. [c.74]
Устранение нестационарности и стандартизация радов. Значительная часть известных методов предназначена для анализа стационарных процессов, статистические свойства которых с течением времени не меняются. Но ряды часто имеют нестационарный характер. Нестационарность рядов можно устранить следующим образом 1) вычесть тренд, т.е. изменения среднего значения, представленного некоторой функцией, которую подбирают путем регрессионного анализа 2) провести фильтрацию рядов специальным фильтром. [c.102]
Большая часть работ по сглаживанию и прогнозу основана на предположении, что исходные случайные процессы, представляющие полезный сигнал и иомехи, стационарны. Это значит, по существу, что статистические -свойства сигнала и иомехи не меняются со временем. Другими словами, предположение стационарности означает, что статистические закономерности случайных процессов, установленные при изучении их поведения в прошлом, сохраняются и в будущем. Предположение стационарности, обычно приемлемое при решении технических задач, не может быть использовано для составления долгосрочных экономических прогнозов, для предсказания погоды на длительный период и для экстраполяции случайных процессов, порождающий механизм и тенденция развития которых недостаточно изучены. Методы сглаживания и упреждения стационарных процессов могут быть обобщены и для так называемых квазистационарных процессов, статистические характеристики которых медленно меняются во времени. В соответствии с теорией фильтрации и прогноза квазистационарных процессов могут быть построены сглаживающие и упреждающие фильтры с медленно изменяющимися параметрами, оптимальные для локальных статистик. Как мы увидим далее, ряд качественных выводов теории сглаживания и экстраполяции сохраняет силу и в нестационарном случае. [c.301]
Моделирование при помощи нестационарных рядов может оказаться проблематичным, например, это может привести к ложной корреляции. Чтобы понять, что это такое, взгляните на рис. 7.7, на котором изображены значения индексов FTSE 100 и S P 500. Коэффициент корреляции этих двух рядов равен 0,81. Однако было бы неуместным предполагать причинную связь между значениями индексов. Конечно, оба индекса вместе возрастают и падают на протяжении длительных периодов времени, но является ли рост одного индекса причиной роста другого В действительности же, в соответствии с экономической теорией, причиной одновременного роста индекЛов служит долгосрочный экономический рост в обеих странах при условии высокого уровня интегрированное национальных экономик и положительного уровня инфляции. Таким образом, причиной долго- [c.322]
Метод Муира. Данный метод используется в случае прогнозирования нестационарного спроса [33, с. 36]. Здесь предполагается, что изменение среднего ряда (уравнение (7.6)) зависит от времени не линейно, а пропорционально значению среднего р., т. е. зависит линейно в логарифмах. Тогда мультипликативная модель будет выражена уравнением [c.128]
