NB Средняя стоимость запасов может быть рассчитана с помощью модели Баумоля [c.202]
Наиболее популярная теория спроса на деньги, рассматривающая его с точки зрения оптимизации денежных запасов, основана на выводах к которым пришли независимо друг от друга Уильям Баумоль и Джеймс Тобин в середине 50-х гг. Сегодня эта теория широко известна как модель Баумоля—Тобина. Они указывали, что индивиды поддерживают денежные запасы также, как фирмы поддерживают товарные запасы. В любой данный момент домашнее хозяйство держит часть своего богатства в форме денег для покупок в будущем. [c.452]
Одновременно можно получить алгебраическое выражение спроса на деньги в модели Баумоля—Тобина. Это уравнение интересно тем, что позволяет представить спрос на деньги как функцию трех ключевых параметров дохода, процентной ставки и постоянных издержек [c.454]
Существуют теории спроса на деньги, особо выделяющие такую функцию денег, как средство обращения. Эти теории называются теориями трансакционного спроса на деньги. В них деньги играют роль подчиненного актива, накапливаемого лишь с целью совершения покупок. Так, в модели Баумоля — Тобина анализируются выгоды и издержки хранения наличных денег. Выгода состоит в отсутствии необходимости посещать банк при совершении каждой покупки (сделки). Общие же издержки определяются недополучением процентов по возможным сберегательным счетам (г), а также затратами времени клиента на посещение банка из расчета его заработка (F). Если У— это запланированный индивидуумом объем годовых расходов на покупки, то в начале года эта сумма будет равна У, в конце года — 0, а среднегодовое ее значение — У/2. Если индивидуум посещает банк не один раз в год, а N раз, то среднегодовое значение суммы наличных денег у него на руках составит Y/(2xN). Недополученные им проценты составят (гхУ)/(2х.Ы), а издержки посещения банка будут равны FxN. Чем больше число посещений банка (N), тем выше связанные с этим издержки, но тем меньше сумма недополученных процентов. [c.126]
Модель Баумоля. По замечанию У. Баумоля, остаток денежных средств на счете во многом сходен с остатком товарно-материальных запасов, поэтому для его оптимизации может быть использована модель оптимальной партии заказа. Оптимальный размер средств на счете определяется с использованием иных переменных С — сумма денежных средств, которая может быть получена от продажи ликвидных ценных бумаг или в результате займа С/2 — средний остаток средств на счете С — оптимальная сумма денежных средств, которая может быть получена от продажи ликвидных ценных бумаг иди в результате займа С /2 — оптимальный средний остаток средств на счете F — трансакционные издержки по купле-продаже ценных бумаг или обслуживанию полученной ссуды на одну операцию Т — общая [c.302]
Так, в соответствии с моделью Баумоля остатки ДА на предстоящий период определяются в следующих размерах [c.359]
Наиболее широко используемой в этих целях является Модель Баумоля, который первый трансформировал для планирования остатка денежных средств ранее рассмотренную Модель EOQ. Исходными положениями Модели Баумоля является постоянство потока расходования денежных средств, хранение всех резервов денежных активов в форме краткосрочных финансовых вложений и изменение остатка денежных активов от их максимума до минимума, равного нулю (рис. 5.17.) [c.165]
Рисунок 5.17. формирование и расходование остатка денежных средств в соответствии с Моделью Баумоля. [c.165]
С учетом потерь рассмотренных двух видов строится оптимизационная Модель Баумоля, позволяющая определить оптимальную частоту пополнения и оптимальный размер остатка денежных средств, при которых совокупные потери будут минимальными (рис. 5.18.) [c.166]
Математический алгоритм расчета максимального и среднего оптимальных размеров остатка денежных средств в соответствии с Моделью Баумоля имеет следующий вид [c.167]
Пример необходимо определить на основе Модели Баумоля средний и максимальный размер остатков денежных средств на основе следующих данных планируемый годовой объем денежного оборота предприятия составляет 225 тыс. усл. ден. eg. расходы по обслуживанию одной операции пополнения денежных средств составляют 100 усл. ден. eg. среднегодовая ставка процента по краткосрочным финансовым вложениям составляет 20%. [c.167]
Несмотря на четкий математический аппарат расчетов оптимальных сумм остатков денежных активов обе приведенные модели (Модель Баумоля и Модель Миллера — Орра) пока еще сложно использовать в отечественной практике финансового менеджмента по следующим причинам [c.170]
В соответствии с моделью Баумоля определяются [c.254]
Примем номинальный доход, получаемый экономическим субъектом за месяц, равным У. В модели Баумоля-Тобина спрос на деньги зависит от уровня потребления и предполагается, что весь доход Y расходуется им в течение месяца для покупок. На первый взгляд самое простое решение проблемы — сохранять весь полученный доход в виде наличных денег. При равномерном их расходовании в течение месяца график спроса на деньги будет иметь вид нисходящей прямой (рис. 6.1). По истечении месяца субъект снова получит доход, равный У, и снова будет его постепенно расходовать и т.д. 150 [c.150]
Оптимальный уровень денежных средств прогнозируется с помощью моделей Баумоля и Миллера-Ор-ра. [c.68]
| Рис. 6.3. График изменения остатка средств на расчетном счете (модель Баумоля) | 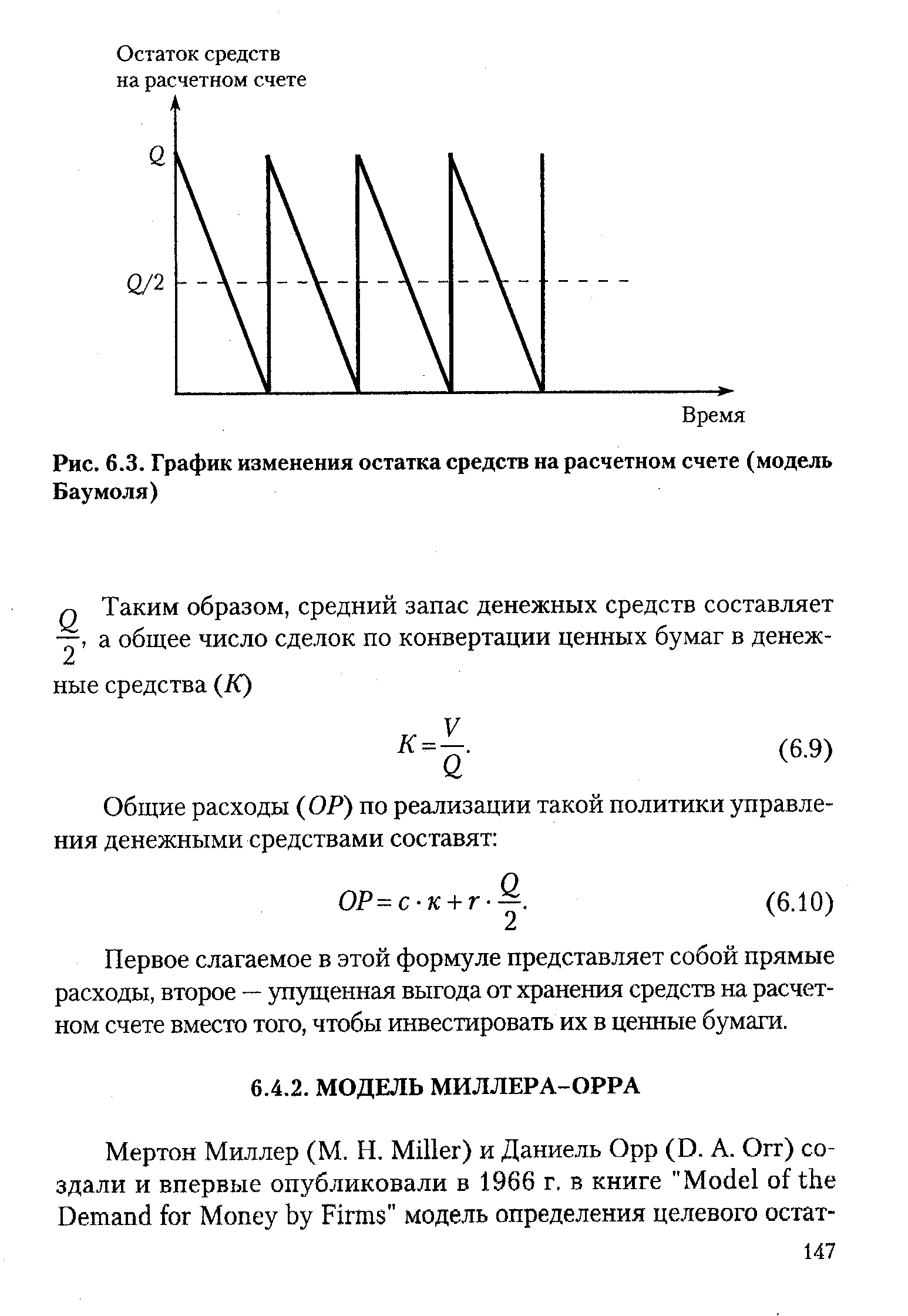 |
В чем принципиальное отличие модели Баумоля от модели Миллера- Орра [c.154]
Модель Баумоля — алгоритм, позволяющий оптимизировать размер среднего остатка денежных активов предприятия с учетом объема его платежеспособного оборота, средней ставки процентного дохода по краткосрочным финансовым вложениям и средней суммы затрат по операциям краткосрочного инвестирования. [c.268]
В западной практике финансового менеджмента применяются более сложные модели управления денежным потоком. Это модель Баумоля и модель Миллера—Орра, разработанные соответственно в 1952 и 1966 гг. Однако применение этих моделей в России в нынешних рыночных условиях (высокий уровень инфляции, возрождающийся фондовый. рынок, колебания ставок рефинансирования ЦБ и др.) пока не представляется возможным. [c.130]
Модель Баумоля. Предположим, что организация имеет некоторую сумму денежных средств, которую постоянно расходует на оплату счетов поставщиков и т.п. Чтобы вовремя оплачивать счета, коммерческая организация должна обладать определенным уровнем ликвидности. В качестве цены за поддержание необходимого уровня ликвидности принимают возможный доход от инвестирования среднего остатка денежных средств в государственные ценные бумаги. Основанием для такого решения служит допущение, что государственные ценные бумаги являются безрисковыми (т.е. их степенью риска можно пренебречь). Денежные средства, поступающие от реализации продукции (товаров, работ, услуг), коммерческая организация вкладывает в государственные ценные бумаги. В тот момент, когда денежные средства заканчиваются, происходит пополнение запаса денежных средств до первоначальной ве- [c.236]
При взятии домохозяйством всей необходимой суммы с помощью одного масштабного изъятия М = Р х Q им обеспечиваются собственные потребности, но теряются проценты. В модели Баумоля — Тобина мы можем получить алгебраическое выражение спроса на деньги MD = М/2. Особенность уравнения заключается в том, что оно позволяет представить спрос на деньги (при пересчете на одно посещение банка) как функцию, состоящую из трех ключевых параметров постоянных издержек РЬ, дохода Q, процентной ставки г [c.654]
В модель Баумоля заложено, что фирма при появлении излишка денег на счете сверх рассчитанной суммы оптимального запаса использует его для покупки краткосрочных ценных бумаг в целях получения дохода, а при снижении запаса денег продает часть этих бумаг, повышая запас денег до оптимального уровня. [c.88]
Модель Баумоля пригодна для стабильных предсказуемых денежных расходов и поступлений, она не учитывает сезонных или случайных колебаний, т. е. в ней упрощена реальная ситуация. Позднее были разработаны другие модели, учитывающие ежедневную изменчивость денежных потоков (например, модель Миллера-Орра, 1966). Тем не менее, все формализованные модели имеют определенные ограничения, поэтому в практике управления денежными средствами их используют как вспомогательные для установления оптимального объема денежных средств. [c.89]
Трансакционный спрос на деньги модель Баумоля- Тобина [c.123]
Обратимся к анализу свойств функции трансакционного спроса на деньги, полученной из модели Баумоля-Тобина. Во-первых, как следует из формулы (4) спрос на деньги отрицательно зависит от ставки процента. Это объясняется тем, что повышение процентной ставки ведет к росту упущенных процентных платежей и тем самым, побуждает индивидуума чаще ходить в банк и держать меньшее количество наличных средств. [c.126]
Помимо рассмотренных выше двух традиционных факторов, влияющих на спрос на деньги, мы можем выделить еще один параметр, который согласно модели Баумоля-Тобина оказывает влияние на [c.126]
Таким образом, скорость обращения денег положительно зависит от номинальной ставки процента. Влияние реального дохода на скорость обращения денег зависит от эластичности спроса на деньги по доходу. Если бы эта эластичность равнялась единице, то спрос на деньги был бы пропорционален доходу и не влиял бы на скорость обращения денег. При эластичности, меньшей единицы (которую мы получили в модели Баумоля-Тобина) спрос на деньги изменяется в меньшей степени, чем доход и мы получаем положительную зависимость между скоростью обращения денег и доходом. [c.135]
Основные методы планирования потребности предприятия в средствах для образования незавершенного производства, готовой продукции и отвлечения средств в расчеты. Кредиторская и дебиторская задолженности, наличные средства и методы управления ими. Образование и использование накоплений. Модели Баумоля и Орра. Роль факторинга и его виды. [c.117]
Например, компания AB планирует квартальный расход денежных средств в размере 15 млн. руб. Трансакционные издержки на проведение одной инвестиционной операции составляют 3 тыс. руб. Доходность от проведения инвестиционных операций - 12% годовых, или 3% за квартал. Используя модель Баумола-Тобина, можно определить максимальный остаток средств на счете предприятия, который будет образовываться в день проведения инвестиционных операций [c.240]
Наиболее популярной современной концепцией спроса на деньги, рассматривающей их с трансакционных позиций, является модель Баумоля-Тобина. Трансакционные теории считают, что деньги хранятся экономическими субъектами только как средства платежа (от англ, transa tion — сделка). Проблему, решаемую в модели Баумоля-Тобина, сравнивают с проблемой фирмы, которая определяет, какой уровень запасов ей хранить, чтобы, с одной стороны, обеспечить непрерывность воспроизводства, а с другой стороны, снизить до минимума потери от хранения запасов. [c.150]
Модель Баумоля" (модель оптимально- М Алмакс т. 2, [c.332]
В западной практике наибольшее распространение получили модель Баумола и модель Миллера — Орра. Первая была разработана В. Баумолом (W. Baumol) в 1952 г., вторая — М. Миллером (М. Miller) и Д. Орром (D. Огг) в 1966 г. Непосредственное применение этих моделей в отечественную практику пока затруднено ввиду сильной инфляции, аномальных учетных ставок, неразвитости рынка ценных бумаг и т.п., поэтому приведем лишь краткое теоретическое описание данных моделей и их применение на условных примерах. [c.358]
