| Рис. 5.3. Граф состояния (/+1)-й технологической операции Для решения системы (5.2) необходима матрица переходных вероятностей | 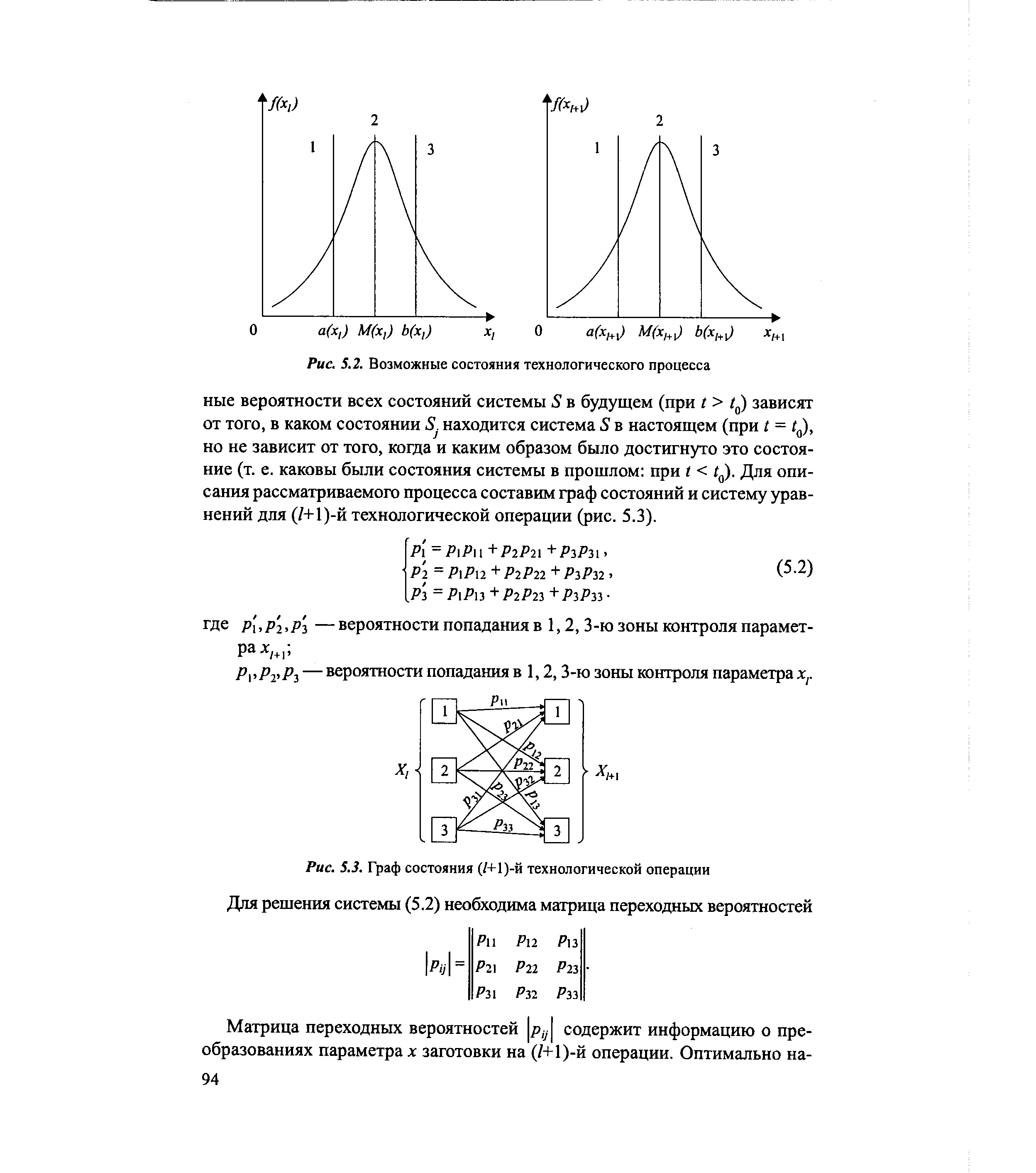 |
Для эффективного использования предлагаемого метода необходимо разработать способ получения матрицы переходных вероятностей Ру без увеличения объема контроля. [c.97]
Используя формулы (5.14) и (5.16), найдем матрицу переходных вероятностей [c.97]
Имея информацию о матрицах переходных вероятностей на всех операциях формирования параметра 7 (рис. 5.1), можно, используя данные одной контрольной операции и методы, описанные в главе 4, прогнозировать состояние ТП. Это расширяет возможности предельного контроля, повышает его эффективность, дает дополнительную информацию для принятия управляющего воздействия на ТП. [c.102]
Интенсивность перехода Я,/ и ц, зависят от текущего состояния системы. Для системы ПО X/ означает интенсивность возникновения (проявления), а ц, — интенсивность устранения ошибок. Следовательно, полная матрица переходных вероятностей системы может быть представлена следующим образом [c.240]
Как известно, цепь Маркова полностью определяется начальным состоянием - вектор-строкой Р(0) - и матрицей переходных вероятностей Р. Состояние на п-м шаге Р " представляется в виде [c.118]
Матрицу переходных вероятностей можно построить разными способами в зависимости от целей исследования. Несмотря на всю условность этого понятия, введем понятие "отказа системы", связав с ним некоторое поглощающее состояние а>. Будем считать, например, что недопустим выход из строя более 3 агрегатов на одной ДКС. Тогда переходные вероятности будут определяться следующим правилом [c.118]
Матрица (2.3) называется переходной или матрицей переходных вероятностей. [c.44]
По главной диагонали матрицы переходных вероятностей стоят вероятности Ри того, что система не выйдет из состояния Sh а останется в нем. [c.45]
Если для однородной марковской цепи заданы начальное распределение вероятностей (2.2) и матрица переходных вероятностей Py (2.3), то вероятности состояний системы P, k) (i = l,n j =l,n) определяются по рекуррентной формуле [c.45]
Используя матрицу переходных вероятностей, определим вероятности состояний Pt(K) после первого шага (после первых суток) [c.46]
В начальный момент времени ЭВМ полностью исправна (состояние iSj). Проверка ЭВМ производится в фиксированные моменты времени fj, /2> /3- Процесс, протекающий в системе S, может рассматриваться как однородная марковская цепь с тремя шагами (первая, вторая, третья проверки ЭВМ). Матрица переходных вероятностей имеет вид [c.46]
Матрица переходных вероятностей имеет вид [c.73]
Запишите матрицу переходных вероятностей и найдите вероятности состояний после двухмесячной эксплуатации. [c.77]
Марковские цепи 43, 48 Матрица переходных вероятностей 44 [c.425]
Пример 3. Две машины А и В сдаются в аренду по одной и той же цене. Эти машины имеют следующие матрицы переходных вероятностей [c.155]
Из этого определения следует, что каждый элемент стохастической матрицы не больше 1. Таким образом, матрица переходных вероятностей является стохастической. [c.25]
Имея в своем распоряжении начальное распределение вероятностей и матрицу переходных вероятностей, можно вычислить вероятности состояний системы от любого k-то до ( +1)-го шага, k=l, 2,.... Имеет место следующая теорема. [c.26]
Составим матрицу переходных вероятностей [c.29]
В этом случае переходные вероятности будем обозначать p.(k). Тогда и матрица переходных вероятностей будет зависеть от k [c.37]
Теорема 3.1. Для неоднородной марковской цепи вектор -строка вероятностей состояний от k-го до ( +1)-го шага равна произведению вектор-строки вероятностей состояний от (k-i)-zo до k-го шага на матрицу переходных вероятностей от k-го до (k+l)-zo шага [c.38]
У неоднородной марковской цепи переходные вероятности р. (k) (хотя бы одна из них) и, следовательно, матрица переходных вероятностей P(k) зависят от номера шага k. [c.44]
Допустим, что в условиях задачи 2.1 переходные вероятности зависят от моментов установления процентных ставок. Матрицы переходных вероятностей задаются следующим образом [c.44]
Замечание 3.4. Для применения формулы (3.2) или (3.3) надо составить матрицы переходных вероятностей Р (1), Р (2), Р (3), Р (4), Р (5) и Р (6), используя разметки соответственно графов на рис, 3.5,3.6,3.7,3.8, 3.9 и 3.10 так, как это делалось в примере 2.3. [c.48]
Матрицы переходных вероятностей неоднородной марковской цепи (имеющей 3 возможных состояния), соответствующие четырем шагам, задаются следующим образом [c.48]
Метод анализа состояния технологической операции основан на допущении, что некоторым образом определена матрица оценок переходных вероятностей />/, , позволяющая решить систему уравнений [c.95]
Опытным путем определена матрица оценок переходных вероятностей 0,7 0,2 0,1 [c.103]
Прогнозирование состояния технологического процесса. Используя данные, полученные на первой контрольной операции/j =15, f2 = 65, = 20, и матрицу оценок переходных вероятностей рг , найдем f > /2 > /з Решим систему уравнений [c.104]
В связи с постоянной изменчивостью рынка перед фирмой неизбежно возникает вопрос каким образом менять свою стратегию, чтобы не попасть в кризисную ситуацию В процессе количественного прогнозирования положения на рынке целесообразно воспользоваться аппаратом цепей Маркова [52]. Применение этого аппарата позволяет заранее принять решение при изменении рыночного состояния. В процессе прогнозирования используется переходная вероятность из одного состояния в другое. Переходная вероятность есть элемент матрицы перехода (Р) [c.184]
Переходные вероятности однородной марковской цепи Ру образуют квадратную матрицу размера п х п. Отметим некоторые ее особенности [c.44]
В этой главе мы рассмотрим однородные марковские цепи. Запишем переходные вероятности в виде квадратной матрицы и-го порядка [c.24]
Доказательство. Предварительно отметим, что размер [1хи] вектор-строки (p k-l),. ..,pn(k-l)) и размер [ихи] матрицы Р переходных вероятностей в правой части равенства (2.4) обеспечивают возможность их перемножения, в результате чего получаем вектор-строку размера [1хи]. [c.27]
Поскольку потоки отказов и восстановлений, под воздействием которых происходят переходы системы S из состояния в состояние, являются пуассоновскими, то случайный процесс, протекающий в системе S, является марковским, причем с дискретными состояниями и непрерывным временем. Тогда, обозначая вероятности состояний stt, sl2 s2l и s22 соответственно через ptt(t), pa(t), P21(f) и p22(t) (не путать с обозначениями переходных вероятностей, см. 2), мы можем составить для них либо по графу (рис. 8.1), либо по матрице (см. 4) систему дифференциальных уравнений Колмогорова (см. (4.4)) [c.128]
Наряду с получением переходной матрицы Р важна и другая задача — вычисление вероятности, что система перейдет из состояния 5. в состояние S не непосредственно в результате одного перехода, а после т переходов или, как иногда говорят, через т этапов. [c.149]
Работы Дункана и Ладани получили дальнейшее развитие в [135]. Авторы исследовали модель разладки, в которой имеется определенное число состояний разлаженного процесса, образующих вместе с состоянием налаженного процесса, цепь Маркова с известной матрицей переходных вероятностей. Каждому состоянию соответствует определенный уровень дефектности продукции. [c.136]
Процесс с дискретным временем процесс с непрерывным временем случайная последовательность марковская цепь вероятности состояний переходные вероятности матрица переходных вероятностей вероятности задержки однородная марковская цепь стохастическая матрица двоякосто-хастическая матрица размеченный граф состояний вектор начального распределения вероятностей. [c.32]
Смотреть страницы где упоминается термин Матрица переходных вероятностей
: [c.183] [c.95] [c.96] [c.133] [c.74] [c.75] [c.77] [c.40] [c.25] [c.26]Математические методы моделирования экономических систем Изд2 (2006) -- [ c.44 ]
