Взаимосвязь случайных величин

из "Вводный курс эконометрики "

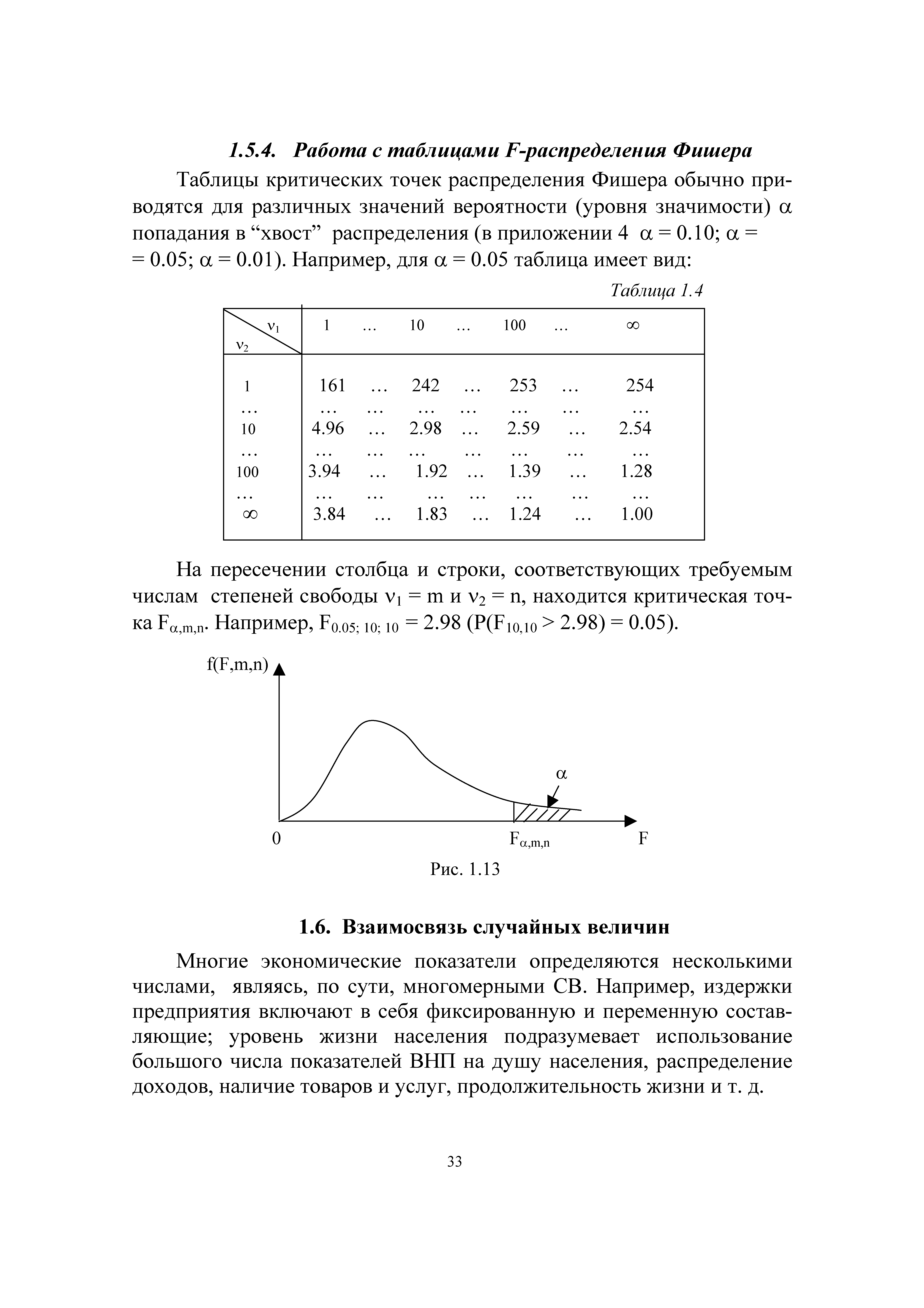
Многие экономические показатели определяются несколькими числами, являясь, по сути, многомерными СВ. Например, издержки предприятия включают в себя фиксированную и переменную составляющие уровень жизни населения подразумевает использование большого числа показателей ВНП на душу населения, распределение доходов, наличие товаров и услуг, продолжительность жизни и т. д. [c.33]
Значения ряда экономических показателей предопределяют величины других показателей. Поэтому одной из центральных задач экономического анализа является задача установления наличия и силы взаимосвязи между различными экономическими показателями (фактически, между СВ). Например, между доходом и потреблением между спросом на товар и его ценой между уровнем инфляции и уровнем безработицы ВНП и уровнем жизни. Вследствие этого при проведении эконометрического анализа одно из главных мест занимает рассмотрение взаимосвязей СВ, при которых реализация одной из них влияет на вероятность определенной реализации другой СВ. [c.34]
Эти условия обычно называют условиями согласованности. [c.35]
Часто построение закона распределения многомерной СВ является задачей достаточно громоздкой и в ряде случаев излишней. Кроме того, информация о каждой из составляющих СВ и о их взаимосвязи в этом случае не является очевидной. Для анализа степени взаимосвязи СВ обычно используют числовые характеристики смешанные моменты распределения, ковариацию и коэффициент корреляции. [c.36]
Зависимость между СВ X и Y, характеризуемая коэффициентом корреляции, называется корреляцией. СВ X и Y называются некоррелированными, если рху = 0, что равносильно равенству аху = 0. Если же рху Ф 0, то СВ X и Y называют коррелированными. [c.37]
Очевидно, при независимости СВ последние слагаемые в данных формулах обращаются в нуль. [c.39]
Значимость коэффициента корреляции при анализе линейной регрессии рассматривается в гл. 4 данного пособия. [c.39]
Пример 1.3. На основе многолетних наблюдений за результатами вложений в две компании был построен закон распределения СВ X и Y - размеров годовых дивидендов (в процентах) от вложения в данные отрасли. Закон представлен табл. 1.6. Необходимо определить маргинальные законы распределений каждой из СВ, установить наличие зависимости между ними. Вычислить ковариацию и коэффициент корреляции, а также решить, что менее рискованно вкладывать деньги в одну из этих отраслей либо одновременно в обе в равных пропорциях. [c.39]
В средней части табл. 1.6 приведены совместные вероятности Р(х, у) двух СВ. Например, Р(Х = 20, Y = 5) = Р(20, 5) = р22 = 0.2. В правом столбце и нижней строке приведены вероятности СВ X и Y соответственно. Например, Р(Х = -10) = = РХ(—10) = 0.6. Условная вероятность Р(х у) определяется по столбцам данной таблицы, а условная вероятность Р(у х) - по строкам. Например, Р(20 Y = 5) = = Р(Х = 20, Y = 5) / P(Y = 5) = 0.2/0.45 = 0.444. [c.39]
Определим их ковариацию и коэффициент корреляции. [c.39]
Таким образом, можно сказать, что между X и Y существует не очень сильная отрицательная линейная зависимость. Риски от вложения в акции компаний можно определять по разбросу значений их дивидендов, т. е. по дисперсиям СВ. Следовательно, можно сделать вывод, что вложение в первую компанию более рискованно, чем во вторую (D(X) = 216 55.6875 = D(Y)). [c.40]
Поскольку D(Z) = 45.989 55.6875 = D(Y), то есть основания считать, что одновременное вложение в обе отрасли в равных пропорциях является наименее рискованным из трех рассмотренных вариантов вложений. [c.40]

Вернуться к основной статье