Номинальная и эффективная нормированные ставки

из "Финансовая математика "

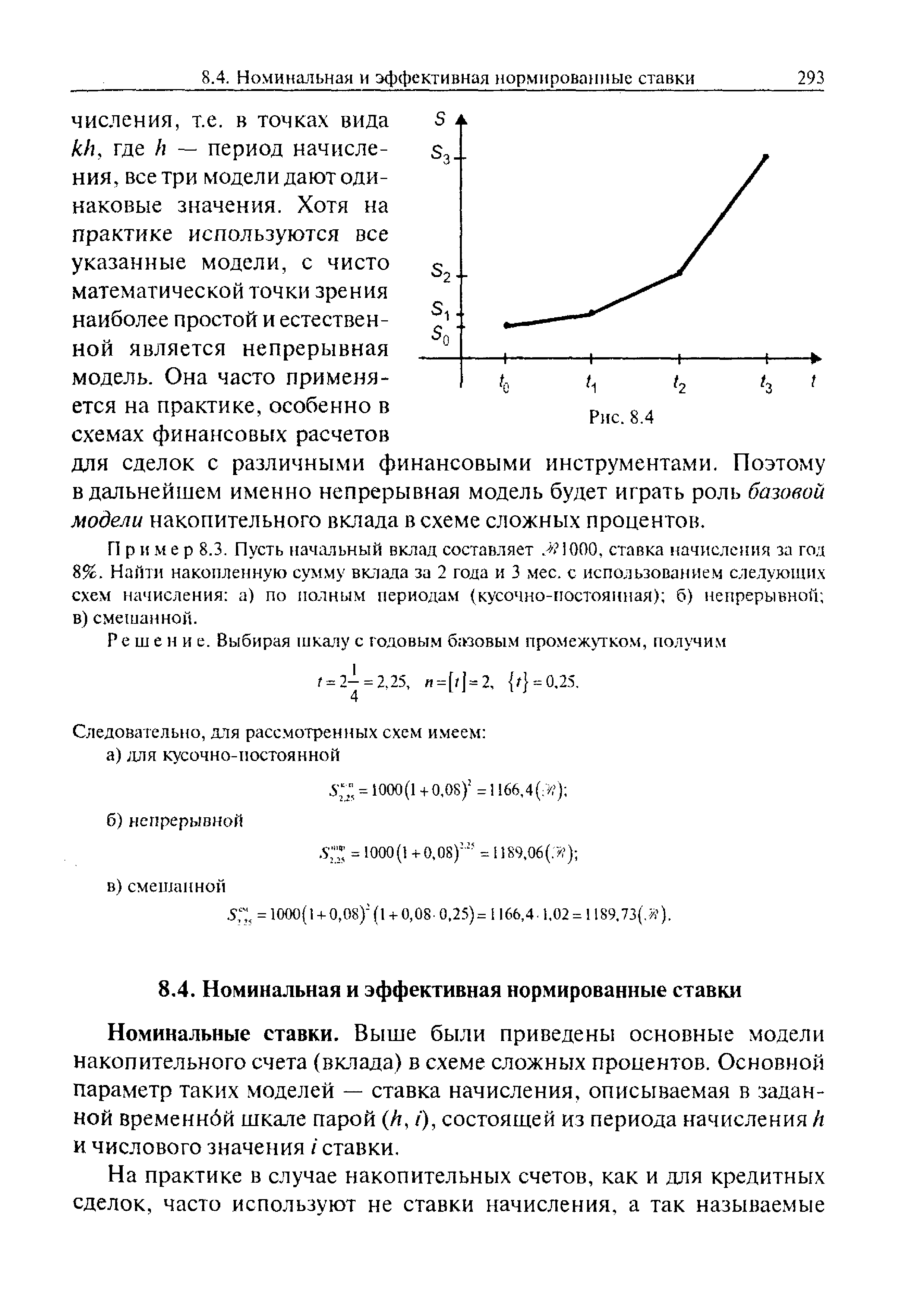
Пример 8.3. Пусть начальный вклад составляет ЮОО, ставка начисления за год 8%, Найти накопленную сумму вклада за 2 года и 3 мес. с использованием следующих схем начисления а) по полным периодам (кусочно-постоянная) б) непрерывной в) смешанной. [c.293]
Таким образом, нормированные номинальные ставки в накопительных схемах сложных процентов вполне аналогичны нормированным ставкам простых кредитных сделок и нормированным ставкам начисления в схеме простых процентов. Во всех случаях идея состоит в приведении (нормировании) ставок, непосредственно связанных с различными периодами, к некоторым стандартным (например, базовым), периодам. [c.294]
Поскольку роль номинальной ставки — стандартизированное представление ставок начисления, то ее задание предполагает, кроме указания номинального периода и значения самой ставки, задание дополнительной информации, позволяющей легко определить соответствующий период начисления, а также правило для вычисления значения ставки начисления. [c.294]
Иногда понятие номинальной ставки вводят несколько иначе, основываясь на так называемой кратной выплате процентов. Этот подход можно пояснить следующим образом. [c.294]
Целое число т, т.е. число фактических начислений за исходный номинальный период, назовем кратностью начисления. [c.296]
Иными словами, ставка за фактический период начисления в т раз меньше ставки за номинальный период. [c.296]
Формально номинальная ставка в заданной временной шкале Т задается тройкой (/ , А, у ), где b — длина (номинального) периода h — длина периода начисления ./— числовое значение номинальной ставки. [c.296]
Другой способ задания номинальной ставки состоит в задании тройки (Ь, /и, у), где b и j имеют тот же смысл, что и выше, а т — кратность начисления, т.е. [c.296]
Пример 8.4. Пусть в годовом шкале номинальная ставка имеет вид -, —, 12%. [c.297]
Найти кратность и ставку начисления. [c.297]
Использование скобок позволяет отличать номинальную ставку от ставки начисления, которую обозначаем как /Л. [c.298]
В этом случае мы пишем просто /. [c.298]
Важно понимать, что нормированная номинальная процентная ставка относится к единичному (базовому) промежутку временной шкалы. На практике это обычно годовая ставка, тогда как ставка начисления это ставка за период начисления. [c.300]
Как уже упоминалось, мы будем работать исключительно с непрерывной моделью. В дальнейшем ограничимся формулировкой результатов для этой модели в терминах номинальной ставки лишь для ставки Iм с /я-кратным начислением, имея при этом в виду, что запись аналогичных формул в терминах номинальной ставки / получается тривиальной заменой /(ml на / и /т на Л. [c.301]
Прежде чем перейти к изучению непрерывной модели, напомним еще раз, что номинальная ставка является просто нормированным представлением ставки начисления, т.е. приведением ее к единичному периоду временной шкалы и, следовательно, ее удобно использовать, когда рассматривается не одна, а несколько или много ставок начисления. [c.301]
О бесконечно-кратном или непрерывном начислении будет более подробно сказано ниже, а сейчас вернемся к дискретным схемам начисления (с конечной кратностью). [c.302]
Строго говоря, такое определение эффективной ставки в данном случае не вполне обоснованно, так как ранее оно было дано лишь для случая целочисленной кратности начисления за единичный период временной шкалы, т.е. когда т = /h — целое число. [c.306]

Вернуться к основной статье