Двойственность в нелинейном программировании

из "Математические исследования операций в экономике "

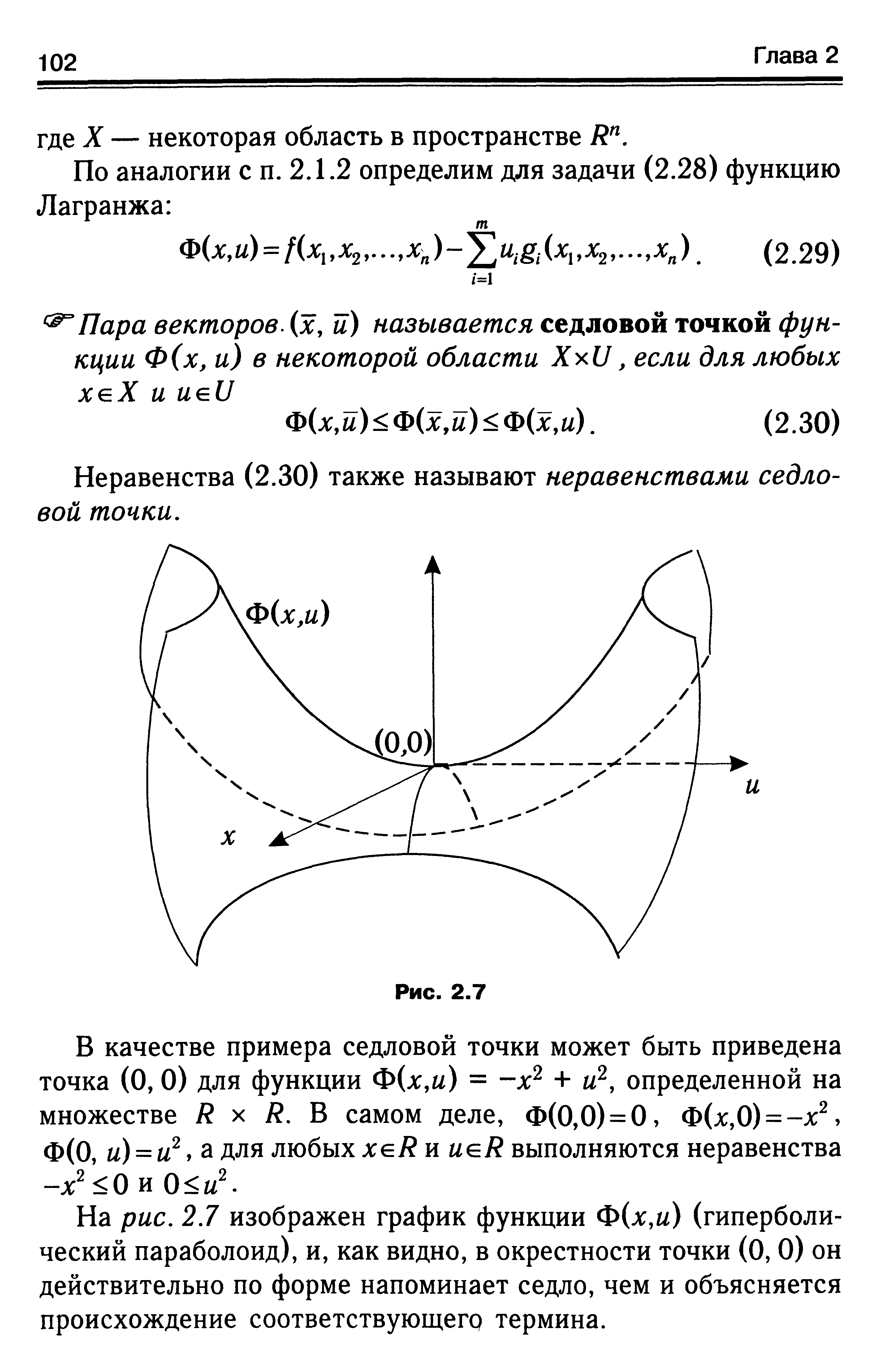
Неравенства (2.30) также называют неравенствами седло-вой точки. [c.102]
На рис. 2.7 изображен график функции Ф(х,и) (гиперболический параболоид), и, как видно, в окрестности точки (0, 0) он действительно по форме напоминает седло, чем и объясняется происхождение соответствующего термина. [c.102]
Теорема 2.3. (Достаточное условие экстремума). [c.103]
Из того, что для всех /el m выполняются неравенства следует, что х является допустимым планом задачи (2.28). [c.103]
Вообще говоря, существуют разные варианты необходимого условия Куна — Таккера. Приведем один из них. [c.105]
Теорема 2. 4. (Необходимое условие наличия экстремума). [c.105]
Если (D /) является задачей выпуклого программирования с решением х, ее целевая функция f(x) и функции ограничений g x) — дифференцируемы, нелинейные ограничения в форме неравенств удовлетворяют условию регулярности Слейтера, то существует такой вектор и 0, что (х,и) — седловая точка функции Лагранжа Ф(х,и). [c.105]
Мы не будем здесь приводить доказательство теоремы (2.4), которое является довольно сложным. Заинтересованный читатель может найти его в таких источниках, как [1, 13]. [c.105]
Значение теоремы Куна — Таккера состоит в том, что она позволяет связать процесс решения оптимизационной задачи с поиском седловых точек функции Лагранжа, т. е., грубо говоря, с максимизацией этой функции по х и минимизацией по и. [c.105]

Вернуться к основной статье