Обобщение по признакам

из "Ситуационное управление теория и практика "

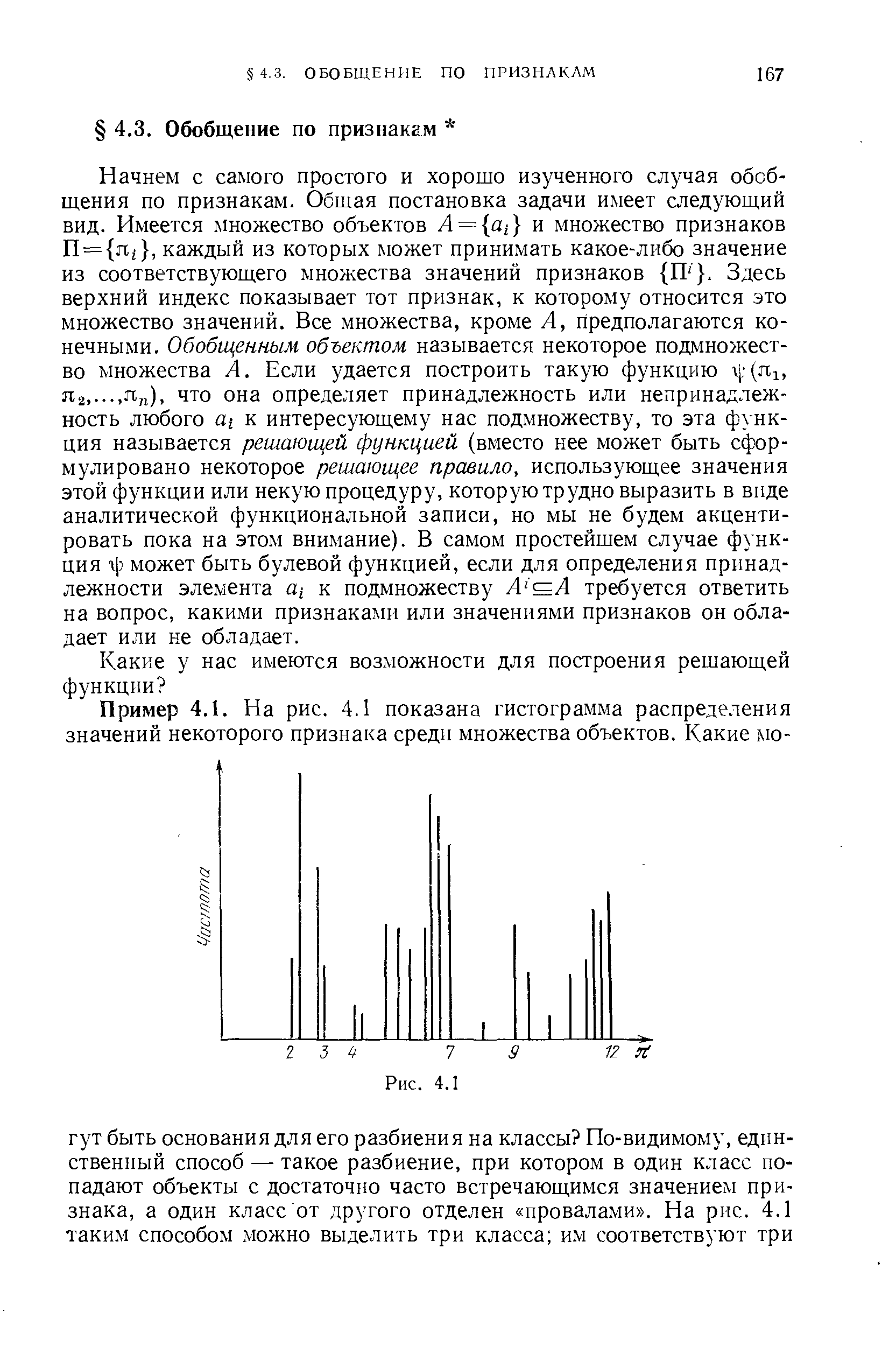
Начнем с самого простого и хорошо изученного случая обобщения по признакам. Общая постановка задачи имеет следующий вид. Имеется множество объектов A = at и множество признаков П = яг , каждый из которых может принимать какое-либо значение из соответствующего множества значений признаков П7 . Здесь верхний индекс показывает тот признак, к которому относится это множество значений. Все множества, кроме А, предполагаются конечными. Обобщенным объектом называется некоторое подмножество множества А. Если удается построить такую функцию (я1 Яа.пп), что она определяет принадлежность или непринадлежность любого ai к интересующему нас подмножеству, то эта функция называется решающей функцией (вместо нее может быть сформулировано некоторое решающее правило, использующее значения этой функции или некую процедуру, которую трудно выразить в виде аналитической функциональной записи, но мы не будем акцентировать пока на этом внимание). В самом простейшем случае функция г ) может быть булевой функцией, если для определения принадлежности элемента а/ к подмножеству А А требуется ответить на вопрос, какими признаками или значениями признаков он обладает или не обладает. [c.167]
На этом принципе построено довольно много методов обобщения понятий, которые можно было бы назвать методами разделения в пространстве признаков. В простейшем случае ситуация, показанная на рис. 4.1, обобщается на пространство произвольной размерности и строятся методы выделения наиболее крупных скоплений объектов, для которых расстояния между признаками значительно меньше расстояний между отдельными скоплениями. На этой идее основано большинство методов, развиваемых в рамках кластерного анализа. [c.168]
Обобщением такого подхода к образованию понятий служит идея использования специальной функции для выделения ядер из заданного множества объектов. Эта функция может быть построена различными способами. Например, она может принимать на объектах, входящих в ядро, значения, значительно превосходящие значения той же функции в некоторой окрестности пространства признаков, окружающей ядро. Эти функции как бы задают распределение потенциалов в пространстве признаков, почему и сам метод работы с такими функциями получил название метода потенциальных функций. [c.168]
Однако подобные методы, основанные на использовании лишь сведений о пространстве признаков и некоторых его свойствах, многократно исследованные в теории распознавания образов, почти ничего не дают для решения задачи формирования понятий, возникающей в теории ситуационного управления и родственных ей подходов к решению проблемы целесообразного управления объектом, И связано это с тем, что в таких условиях мы всегда имеем некоторую априорную информацию о конкретных представителях, входящих в формируемое понятие. Иными словами, мы заранее знаем, что некоторые объекты аг должны входить в формируемое понятие (положительные примеры), а другие аг не должно входить в него (отрицательные примеры). Это приводит к постановке задачи обобщения по признакам на основе обучающей выборки, состоящей из положительных и отрицательных примеров. Именно такие задачи мы и будем изучать ниже в данной главе. [c.168]
Видоизменением метода разделяющих гиперплоскостей являются методы, в которых разделение происходит за счет криволинейных поверхностей. Однако в силу трудностей формирования удачных разделяющих поверхностей второго и более высоких порядков эти методы на практике применения фактически не нашли. [c.170]
Имеется еще группа методов, в которых вместо простого разделения в пространстве признаков используются метрические функции этого пространства. Например, группировка объектов в новое понятие происходит таким образом, что расстояния между парами объектов, попавших в одно понятие, существенно превосходят расстояние от них до объектов, лежащих вне его (разделение по потенциальной функции). [c.170]
Указанный недостаток, несмотря на простоту процедур формирования понятий по методу разделения в пространстве признаков, делает эти методы мало пригодными для задач ситуационного управления. Именно поэтому в системах ситуационного управления, как правило, используются другие принципы формирования понятий и организации классификации. [c.171]
Когда всем объектам сопоставлены наборы двоичных признаков, наступает второй этап. На нем случайным образом генерируются функции от получившихся двоичных аргументов, принимающие также двоичные значения. Число аргументов у этих функций может быть либо фиксированным, либо меняться от 1 до т, где т — число различных двоичных признаков, получившихся после применения предикатов к исходному множеству признаков. Каждая такая функция рассматривается как потенциальное элементарное разделяющее правило. Для обеспечения разделения нужно, чтобы для всех объектов, входящих в число отрицательных примеров в обучающей выборке, эта функция обращалась в нуль, а для всех объектов, входящих в число положительных примеров в той же обучающей выборке, принимала значение 1 хотя бы один раз (но чем больше, тем разделяющее правило лучше). Тогда дизъюнкция таких элементарных разделяющих правил может рассматриваться как окончательное разделяющее правило при условии правильной классификации всех объектов, образующих обучающую выборку. [c.172]
Возможны и другие способы организации общего решающего правила, а также отбора для включения в него элементарных разделяющих правил. Но суть метода от этого не меняется. [c.172]
Проиллюстрируем выполнение описанной процедуры сначала на очень простом примере, в котором исходное множество признаков таково, что они уже являются двоичными. В этом случае первый этап, связанный с применением подходящих предикатов к исходным признакам, отсутствует. [c.172]
Пример 4.2. На рис. 4.4 показана обучающая выборка, состоящая из пяти положительных и четырех отрицательных примеров. [c.172]
В заключение опишем еще один метод формирования понятий на основе призначной структуры, отличающийся по своей идее от ранее рассмотренных. Этот метод носит название метода растущих пирамидальных сетей (РПС-метод). Для нас он интересен не только в качестве еще одного метода обобщения по признакам, но и потому, что он может использоваться при планировании многошаговых решений. И в соответствующей главе книги мы об этом будем говорить. [c.174]
Динамика изменения (роста) РПС задается с помощью специальных правил. [c.175]
Выполнение этого правила иллюстрирует рис. 4.6. Те рецепторы, которые возбудились, зачернены. На рис. 4.6, а показана РПС до применения правила, а на рис. 4.6, б — после его применения. После того, как в соответствии с правилом 1, введены все новые элементы, проверяются условия для применения правила 2 н если они удовлетворяются, то это правило реализуется. [c.176]
Перейдем теперь к процедуре формирования понятий с помощью РПС. В обучающей выборке с двоично кодированными значениями признаков рецептор РПС, соответствующий данному значению некоторого признака, возбуждается, если это значение актуализируется, и не возбуждается в противном случае. На вход РПС последовательно подаются все значения признаков объектов из обучающей выборки как из группы положительных примеров, так и из группы отрицательных примеров. При подаче каждого значения происходит переформирование РПС в соответствии с описанными правилами. [c.176]

Вернуться к основной статье