ПОИСК
Это наилучшее средство для поиска информации на сайте
Предельная норма замещения
из "Теория предельной полезности "
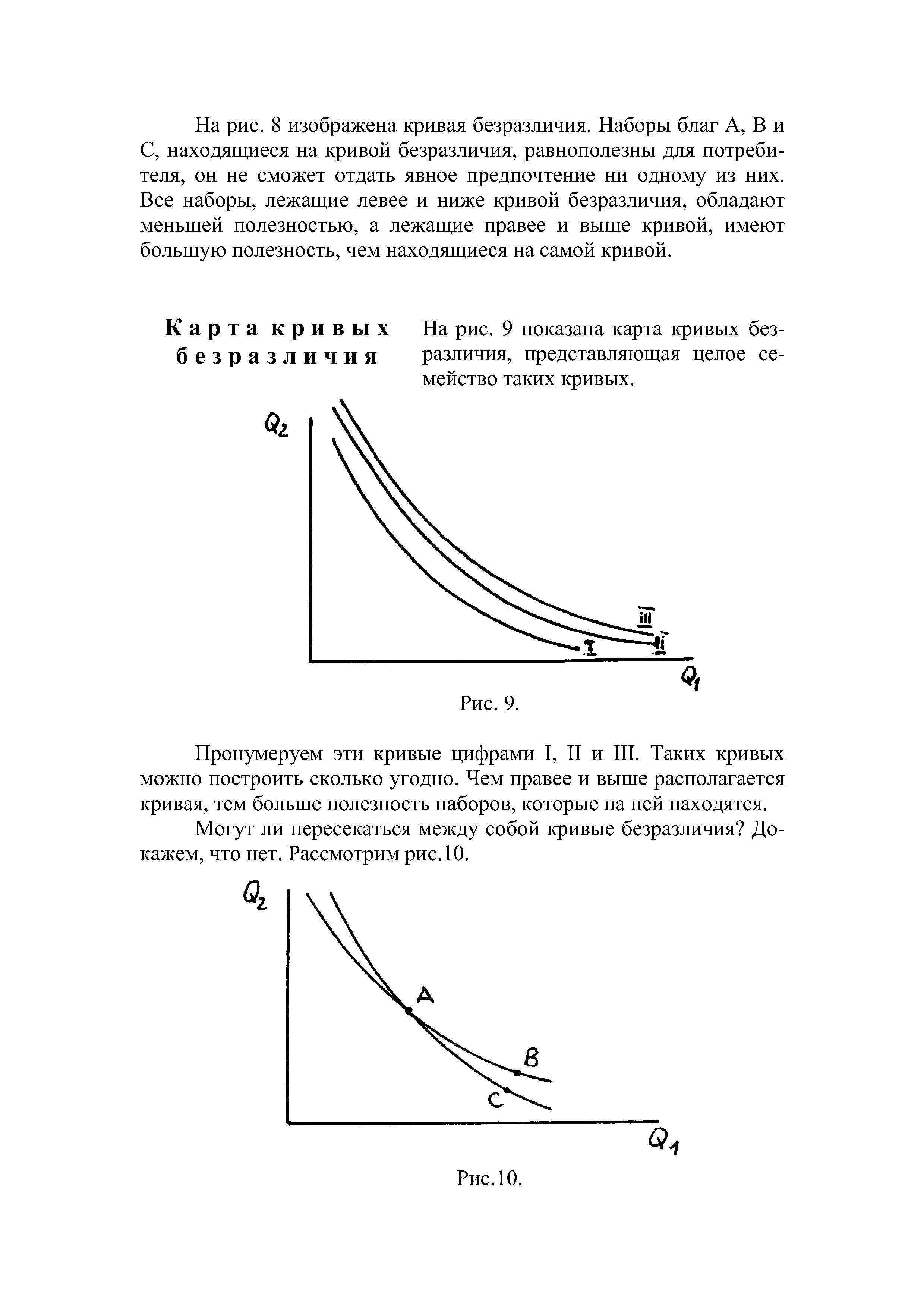
Карта кривых На рис. 9 показана карта кривых без-безразличия различия, представляющая целое семейство таких кривых. [c.20]Пронумеруем эти кривые цифрами I, II и III. Таких кривых можно построить сколько угодно. Чем правее и выше располагается кривая, тем больше полезность наборов, которые на ней находятся. [c.20]
Могут ли пересекаться между собой кривые безразличия Докажем, что нет. Рассмотрим рис.10. [c.20]
Точки А, В и С - наборы благ. Обозначим символами UA, UB и U полезности этих наборов. Так как наборы А и В лежат на одной кривой безразличия, то UA=UB. Но наборы А и С также лежат на одной кривой безразличия и, следовательно, UA=U . Если UA=UB и UA=U , то отсюда следует, что UB=U . Этого быть не может по определению, так как наборы В и С находятся на различных кривых безразличия. Следовательно, наше предположение неверно, и кривые безразличия не могут пересекаться между собой. [c.21]
Могут ли кривые безразличия пересекаться с осями координат Рассмотрим рис. 11. [c.21]
Обозначим через AQi° последнюю порцию первого блага. Если покупатель готов отдать последнюю порцию первого блага (AQi ) за некоторое количество второго блага (AQ2), кривая безразличия будет пересекаться с осью Q2. Но если первое благо таково, что человек без него обойтись не может и ничем его не может заменить, пересечения с осями координат не будет. Например, если набор состоит из воды и хлеба, пересечения не будет, т.к. человек последнюю порцию воды не променяет на сколь угодно большое количество хлеба. Если же набор состоит из взаимозаменяемых благ, пересечение возможно. [c.21]
Переходя от набора А к набору В, потребитель не теряет и не приобретает полезности. Чтобы перейти от набора А к набору В, нужно в наборе А увеличить количество первого блага на AQi, а количество второго сократить на AQ2. Следовательно, в данном случае AQi обладает такой же полезностью, как и AQ2. Обозначим через MRS предельную норму замещения первого блага вторым. Тогда MRS=AQ2/AQL Если приращения AQi и AQ2 будут стремиться к нулю, они превратятся в дифференциалы и формула примет вид MRS=dQ2/dQi. В этом случае MRS будет равна тангенсу угла наклона касательной к кривой безразличия (рис. 13). [c.22]
Обозначим через dUi приращение полезности от добавления dQi, а через dU2 — приращение полезности от добавления dQ2. Выше уже говорилось, что эти приращения полезности равны и противоположны по знаку dUi=-dU2. В выражении MRS=dQ2/dQi правую часть умножим на dUi и разделим на -dU2. Получим MRS= - (dQ2/dQi)(dUi/dU2). Приведем правую часть полученного выражения к виду MRS= dQ2/dQi= -(dUi/dQ2)/(dU2/dQi). Учитывая, что по определению dUi/dQi=MUi, a dU2/dQ2=MU2, где MUi и MU2 -предельные полезности первого и второго благ соответственно, получим окончательную формулу предельной нормы замещения MRS= dQ2/dQi= -MUi/MU2. Это означает, что предельная норма замещения одного блага другим равна обратному отношению их предельных полезностей, взятому со знаком минус. [c.23]
Выведенная формула предельной нормы замещения справедлива для любого набора благ. Уточним ее для оптимального набора, для которого справедливо выражение MUi/Pi=MU2/P2. Получим MUi/MU2=Pi/P2. Подставим полученное выражение в формулу MRS и получим MRS= dQ2/dQi= -Pi/P2. Это значит, что для оптимального набора предельная норма замещения двух благ равна обратному отношению их цен, взятому со знаком минус. [c.23]
Вернуться к основной статье