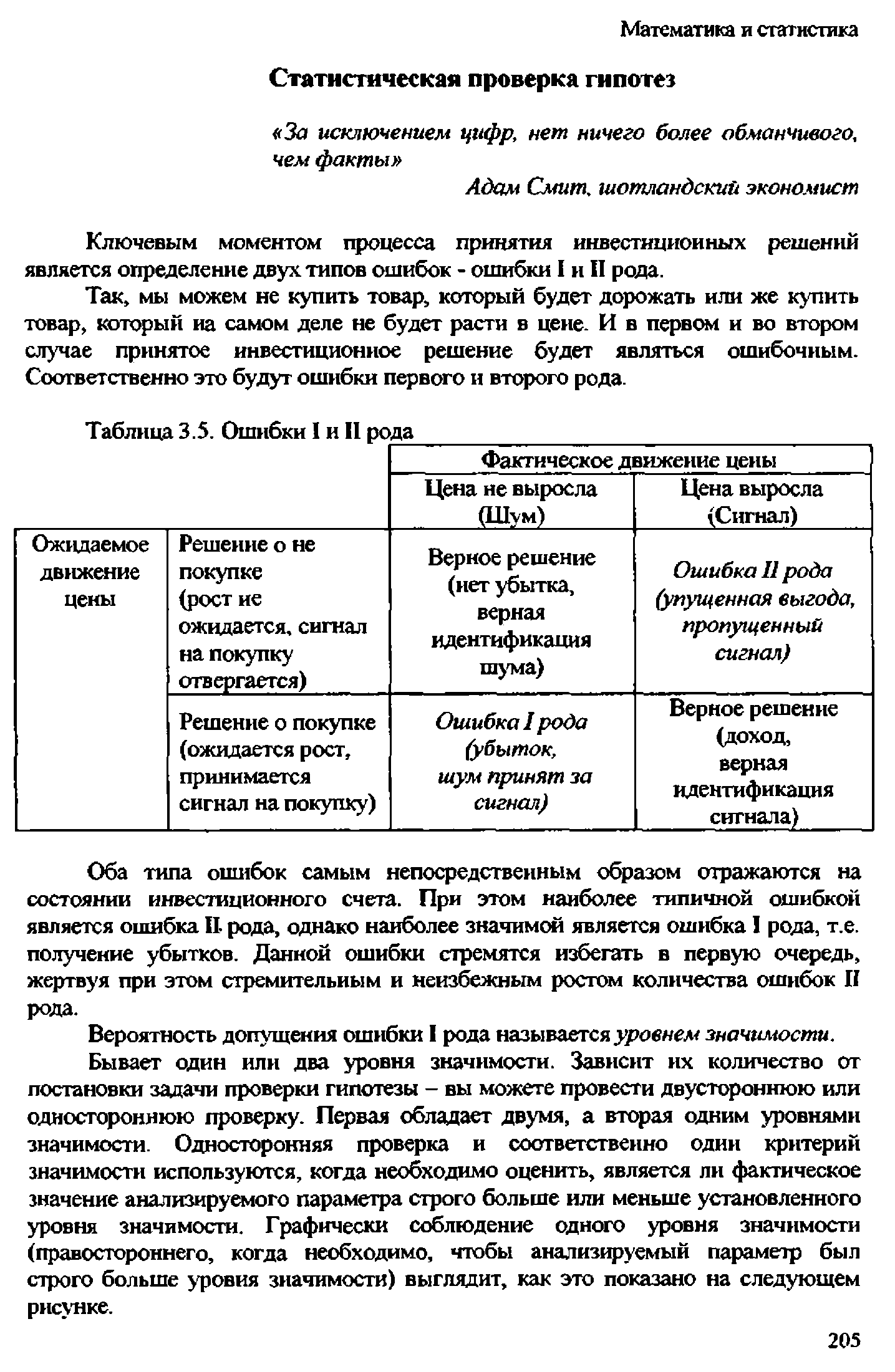
Статистическая проверка гипотез

из "Трейдер-инвестор "

Ключевым моментом процесса принятия инвестиционных решений является определение двух, типов ошибок - ошибки I и II рода. [c.205]
мы можем не купить товар, который будет дорожать или же купить товар, который на самом деле не будет расти в цене. И в первом и во втором случае принятое инвестиционное решение будет являться ошибочным. Соответственно это будут ошибки первого и второго рода. [c.205]
Оба типа ошибок самым непосредственным образом отражаются на состоянии инвестиционного счета. При этом наиболее типичной ошибкой является ошибка II рода, однако наиболее значимой является ошибка I рода, т.е. получение убытков. Данной ошибки стремятся избегать в первую очередь, жертвуя при этом стремительным и неизбежным ростом количества ошибок II рода. [c.205]
Вероятность допущения ошибки I рода называется уровнем значимости. [c.205]
Бывает один или два уровня значимости. Зависит их количество от постановки задачи проверки гипотезы - вы можете провести двустороннюю или одностороннюю проверку. Первая обладает двумя, а вторая одним уровнями значимости. Односторонняя проверка и соответственно один критерий значимости используются, когда необходимо оценить, является ли фактическое значение анализируемого параметра строго больше или меньше установленного уровня значимости. Графически соблюдение одного уровня значимости (правостороннего, когда необходимо, чтобы анализируемый параметр был строго больше уровня значимости) выглядит, как это показано на следующем рисунке. [c.205]
Когда необходимо просто оценить, отличается ли реальное значение анализируемого параметра от фактического, применяется двусторонняя проверка и соответственно два уровня значимости. Графически соблюдение двух уровней значимости выглядит, как это показано на следующем рисунке. [c.206]
Обычно выделяют уровни значимости в 0.1%, 1% или 5%. Если расчетное значение анализируемого параметра (фактическая вероятность допущения ошибки) меньше 5%, то гипотеза может быть явно неверной. Если найденная вероятность меньше 1%, то гипотеза неверна. Если же вероятность меньше 0.1%, то гипотеза практически наверняка неверна. [c.207]
Из регрессии к среднему мы знаем, что частая смена последовательности (например А-Б-А-Б-А-...) событий или знаков, также как ь редкая смена последовательности (А-А-А-А-Б-Б-Б-...), отклоняющаяся в первом случае от нормального 0.5 к 1 и втором - от 0.5 к 0, являются маловероятными на продолжительном промежутке времени и существуют только на коротком. [c.209]
Для расчетов используем закон малых чисел. Применительно к анализ статистических рядов динамики цен закон малых чисел - это вера в то. что выбранная наугад последовательность чисел будет иметь более случайный вид, чем это есть на самом деле. Т.е. если вы попробуете записать предполагаемую последовательность подбрасываний монетки с двумя исходами - орел II IH решка, то она в вашей интерпретации, скорее всего, будет иметь более случайный вид, нежели фактическое подбрасывание. Мы стремимся не отмечать длинные очереди орлов (или решек), переоценивая случайный фактор. Здесь же кроется ошибка начинающих трейдеров, склонных недооценивать случайное блуждание рыночных цен (например, последовательный десятидневный рост). В итоге это приводит к завышенным ожиданиям быстрой остановки тренда, переоценке шансов осцилляторов к скорейшему развороту, т.е. к ожиданиям большей нормальности рынка, чем это ему присуще. [c.209]
Из психологии известно, что люди склонны видеть закономерности в случайных событиях. Однако люди, как правило, умеют отличать случайные ряды от рядов с определенной закономерностью (если они представлены как две альтернативы). В целом же люди видят случайность там, где присутствует структура (ошибка II рода), и структуру там, где была случайность (ошибка I рода). Люди имеют предубеждение против длинных рядов повторений, считая их порождением неких закономерностей. Подготовка в анализе и определении случайных рядов существенно улучшает результат по н. распознаванию. [c.209]
Еще один интересный пример, характерный для вероятностных рядов. [c.209]
Большинство выбирает распределение I, так как люди думают, что случайное распределение должно быть хаотичным и бессистемным. Распределение типа 11 кажется при этом слишком упорядоченным. [c.209]
Дополняет этот пример еще один. [c.209]
Оцените, равны лн вероятности появления 10 бычьих дней из 15 торговых сессий и 100 бычьих дней из 150 торговых сессий для фондового индекса DJ1. [c.210]
Большинство людей скажут, что вероятности этих событий равны. Однако, если исходить из фактических данных распределения динамики фондового индекса, близкого к нормальному, то можно заметить, что вероятность первого события выше, чем второго. Это происходит из-за разных объемов выборки чем больше выборка, тем больше вероятность приближения результатов распределения к нормальному. [c.210]
Ниже приведен пример такого случайного блуждания, который отражает последовательный переход переменной в два возможных состояния +1 или -1 с равной вероятностью 0.5. Накопленный результат 4.5 миллионов последовательных переходов приведен на рисунке. [c.210]
А теперь снова вернемся к нашей гипотезе о том, что динамика фондового индекса DJI является случайной величиной. [c.211]

Вернуться к основной статье