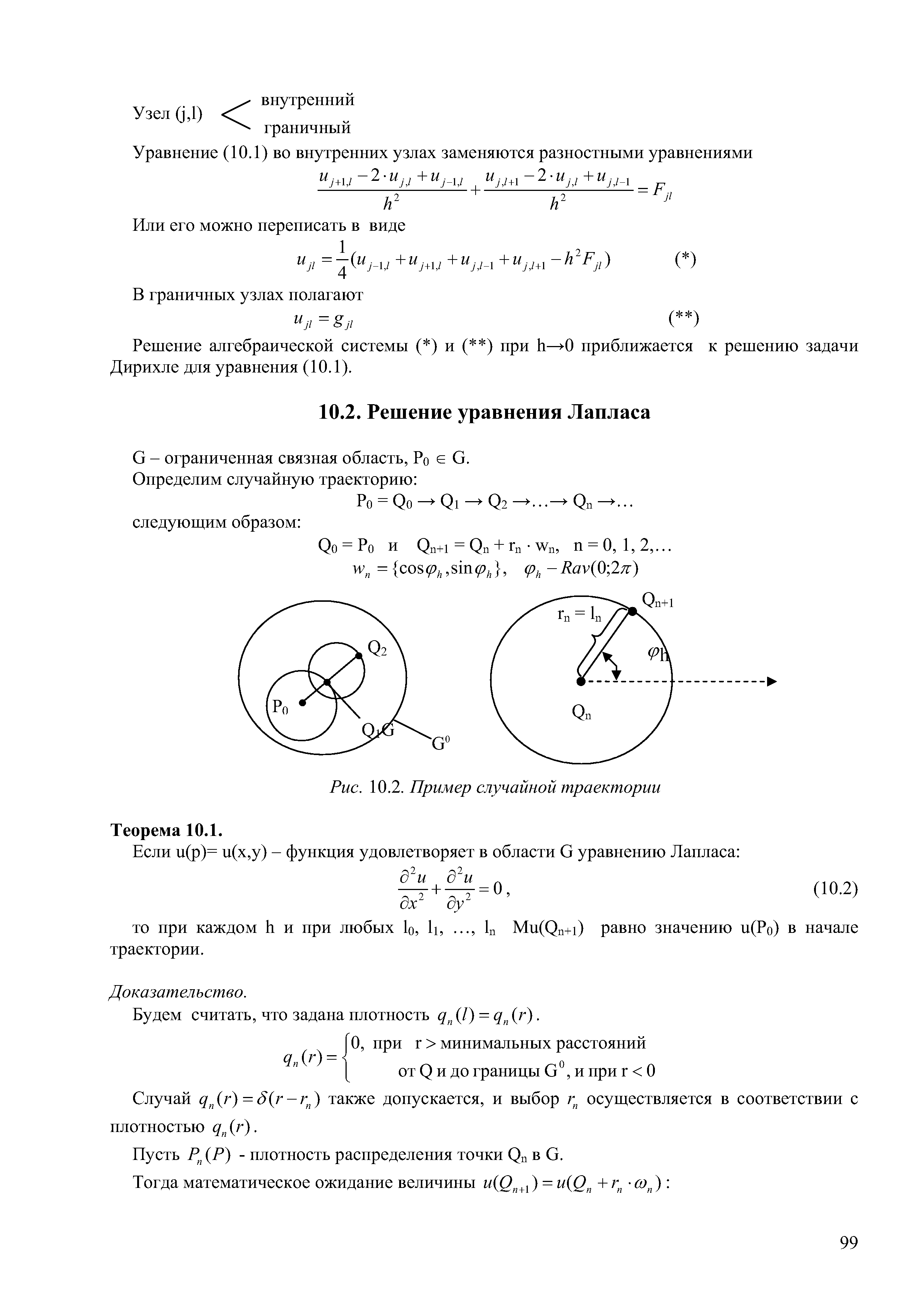
Решение уравнения Лапласа

из "Моделирование и управление в экономике Часть 1 "

Будем считать, что задана плотность qn (/) — qn (r). [c.99]
Случай qn(г) -8(г-гп) также допускается, и выбор гп осуществляется в соответствии с плотностью qn (r). [c.99]
Пусть Рп (Р) - плотность распределения точки Qn в G. [c.99]
Применяя индукцию, получим утверждение теоремы. [c.100]
Построение траекторий рассмотренного типа в трехмерном случае называют блужданиями по сфере. [c.100]
Обозначим U(P) - искомое решение, удовлетворяющее внутри G уравнению (10.2) и обращающееся в g(P) при Р е GQ. [c.100]
Фиксируем достаточно малую окрестность G границы GQ. [c.100]
Чтобы вычислить и(Ро) будем строить траектории вида РО = Qi — Q2 — . .. — пор, пока случайная точка Qv не попадет в G °,. [c.100]
Построив N траекторий такого типа, получим значение (/3у ),g(Pv ).g(Pv ). (10.3) Замечание. Рекомендуется выбирать максимально возможные радиусы гп. [c.100]

Вернуться к основной статье