Эластичность функции

из "50 лекций по микроэкономике Том 2 "

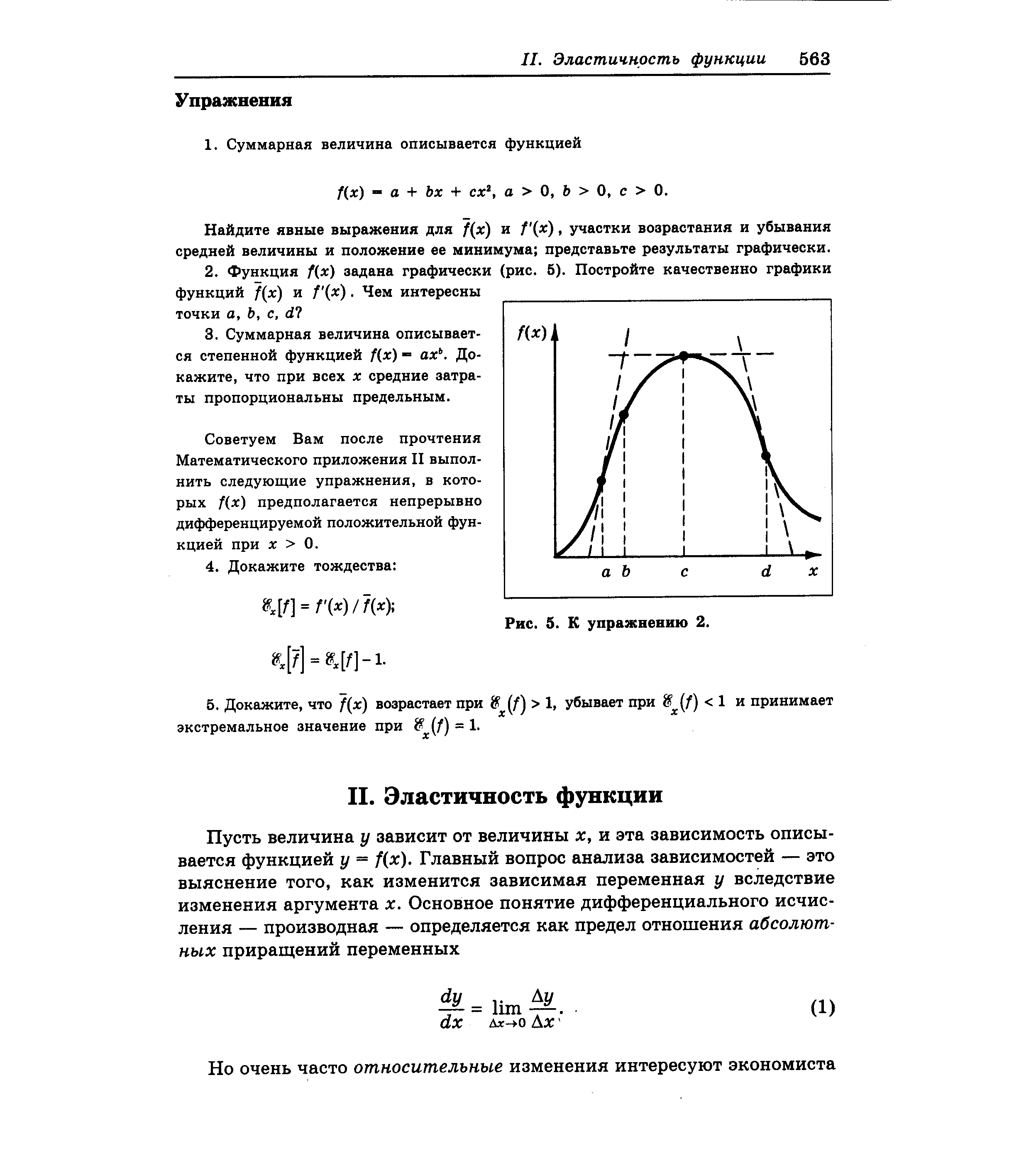
Найдите явные выражения для f(x) и / ( ), участки возрастания и убывания средней величины и положение ее минимума представьте результаты графически. [c.563]
Советуем Вам после прочтения Математического приложения II выполнить следующие упражнения, в которых f(x) предполагается непрерывно дифференцируемой положительной функцией при х 0. [c.563]
Разумеется, относительные отклонения имеют смысл лишь для величин, которые могут принимать только положительные значения. Это относится и к эластичностям. Поэтому дальше мы всюду будем полагать х О, у 0. При этом случаи х = 0 или у = 0 могут рассматриваться только как предельные. [c.564]
Поскольку х и у положительны, знак эластичности всегда совпадает со знаком производной х[у] 0 — для возрастающий функций, ёх[у] 0 — для убывающих. При разных значениях аргумента эластичность может принимать различные значения х[у] 0 — на участках возрастания, %х[у] 0 — на участках убывания функции. [c.564]
В последнем выражении использованы логарифмы по произвольному основанию переход от одного основания логарифмов к другому равносилен умножению на константу и числителя, и знаменателя дроби (4), а это не изменит ее значения. [c.565]
Равенство (4) показывает, что изучение различных свойств эластичности легко свести к изучению соответствующих свойств производных достаточно перейти от величин х и у к их логарифмам. [c.565]
Как можно оценить эластичность функции у = f(x) по ее графику Рассмотрим вначале возрастающую функцию (эластичность при этом положительна). Выберем на графике точку М и проведем через эту точку касательную обозначим А и В — точки пересечения касательной с осями абсцисс и ординат, а С и D — проекции точки М на координатные оси. Допустим, что касательная пересекает ось ординат в отрицательной области, как это показано на рис. 2, а. [c.566]
Все приведенные выкладки и результат (6) полностью применимы и к положению касательной на рис. 2,6. [c.567]
Разница состоит лишь в том, что в первом случае МВ МА, так что он относится к значениям %х[у] 1 во втором случае МВ МА , так что здесь 0 %х[у] 1. При 8Цу] = 1 касательная проходит через начало координат. [c.567]
Мы могли бы применить равенство (6) и к этому случаю, если бы условились считать отношение отрезков положительным, если они направлены в одну сторону (от точки М), и отрицательным — если в противоположные. [c.567]
Рассмотрим теперь эластичность двух видов функций, широко используемых в различных экономических моделях. [c.567]
Следующие утверждения могут быть доказаны читателем как самостоятельные упражнения. [c.568]

Вернуться к основной статье