Принцип максимума Л. С. Понтрягина — необходимое условие оптимальности управления

из "Приближенное решение задач оптимального управления "

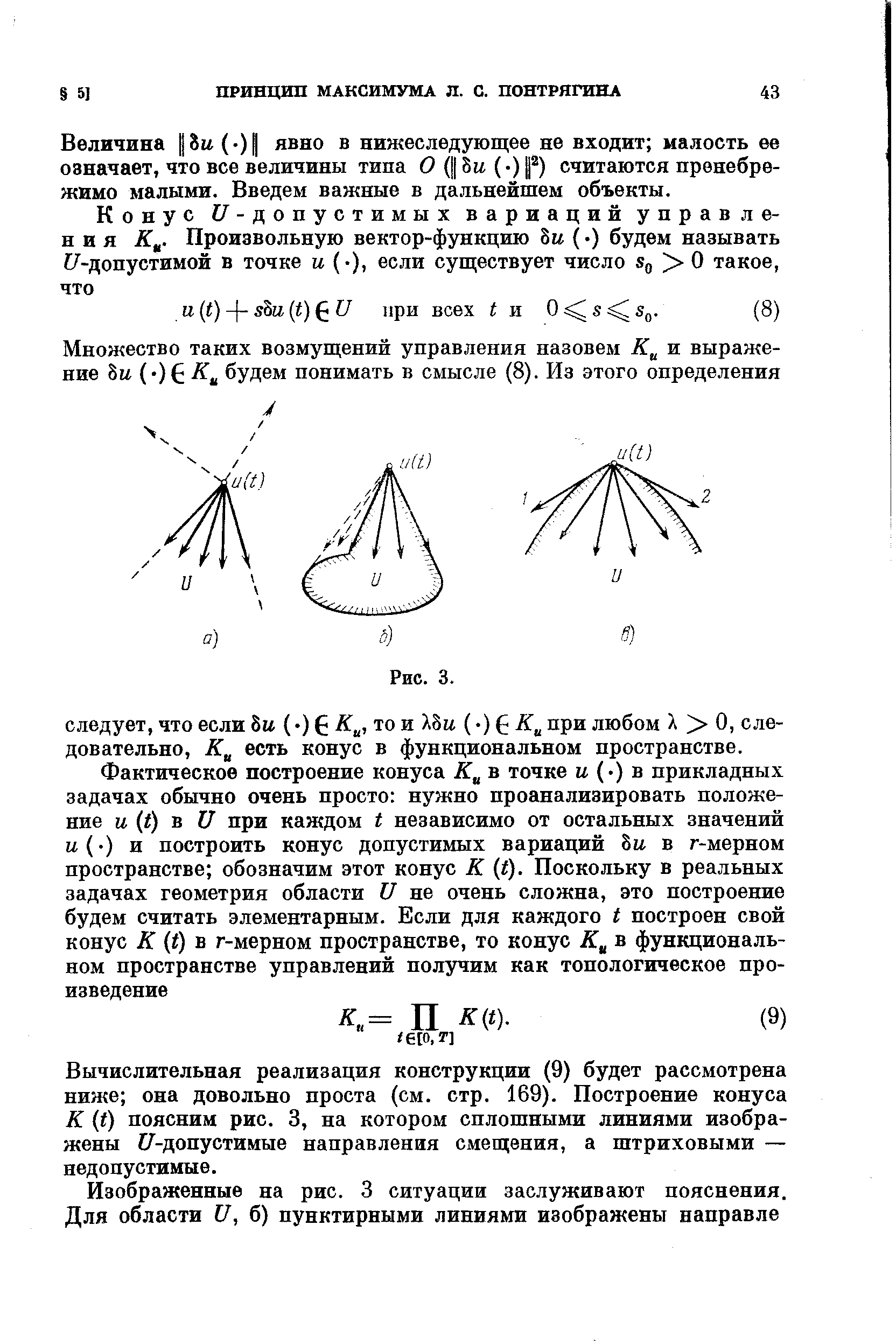
Величина 8и(-) явно в нижеследующее не входит малость ее означает, что все величины типа О ( 8м ( ) 2) считаются пренебрежимо малыми. Введем важные в дальнейшем объекты. [c.43]
Вычислительная реализация конструкции (9) будет рассмотрена ниже она довольно проста (см. стр. 169). Построение конуса К (t) поясним рис. 3, на котором сплошными линиями изображены /-допустимые направления смещения, а штриховыми — недопустимые. [c.43]
Для области U, в) в качестве допустимых изображены направления 1 и 2, касающиеся границы U строго говоря, в смысле определения, данного выше, они недопустимы. Однако если определенный выше конус К (t) замкнуть, эти направления войдут в замыкание К (t). Эту операцию мы будем считать выполненной, Вопрос о влиянии замыкания на содержательную ценность необходимых условий оптимальности, если он оказывается существенным, требует привлечения второй вариации функционалов задачи. [c.44]
Лемма 1. Замыкание конуса смещений Кf является выпуклым конусом. [c.44]
Так как условие 8и ( ) / к есть произведение независимых при разных t условий (t) Kt, то из полученного соотношения следует (W (t)g, 8u(f)) 0 для всех Ha(t) Kt и для всех t [Q, Т] (кроме, может быть, множества меры нуль). [c.47]
Теорема 1 (принцип максимума Л. С. Понтрягина). Пусть и ( ) — оптимальное управление в задаче (1) — (4), Тогда существует некоторый вектор g — 1, g1, g2,. .., gm такой, что определяемая им функция Н [х (t), и, ф (t)] в точке u = u(t) имеет локальный максимум. [c.49]
А такую ситуацию естественно трактовать как неоптимальность траектории и ( ), х ( ) , даже если предельная траектория х (t) и не является решением краевой задачи (1) с каким-то измеримым управлением и (f). [c.51]
В заключение сделаем два замечания. [c.51]
Читатель без труда внесет соответствующие изменения в доказательство. [c.52]
Но при любом заданном ф линейная форма (z, ф) на выпуклом множестве / (х, U) точек локального максимума, не совпадающих с точками глобального максимума, не имеет. Другими словами, точка и, являющаяся точкой локального максимума (/ (х, и), ф), в то же время является и точкой глобального максимума. В следующем параграфе глобальная формулировка (16) будет доказана без предположения о выпуклости / (х, U). [c.53]

Вернуться к основной статье