В принципе выбор определенного соотношения характеризует наклон кривой безразличия только в одной точке. Чтобы расширить представление, необходимо сделать допущение об общей форме кривой безразличия клиента. Обычно делается допущение о том, что клиент имеет постоянную толерантность риска в отношении альтернативных портфелей, которые располагаются вблизи от первоначально выбранной точки. На рис. 24.3 показана природа данного допущения. Как указывается в части (а), когда предполагается, что клиент имеет постоянную толерантность риска, на рисунке кривые безразличия с дисперсией по горизонтальной оси являются линейными. Это означает, что уравнение кривой безразличия такого инвестора является уравнением прямой линии, для которого переменная на горизонтальной линии - это дисперсия ( а2р), а переменная на вертикальной линии - ожидаемая доходность (/ /,) Поскольку уравнение прямой линии имеет вид Y = a + ЬХ, где я — точка пересечения вертикальной оси, a b — наклон, то уравнение кривой безразличия можно записать следующим образом [c.848]
| Рис. 24.3. Постоянная толерантность риска | 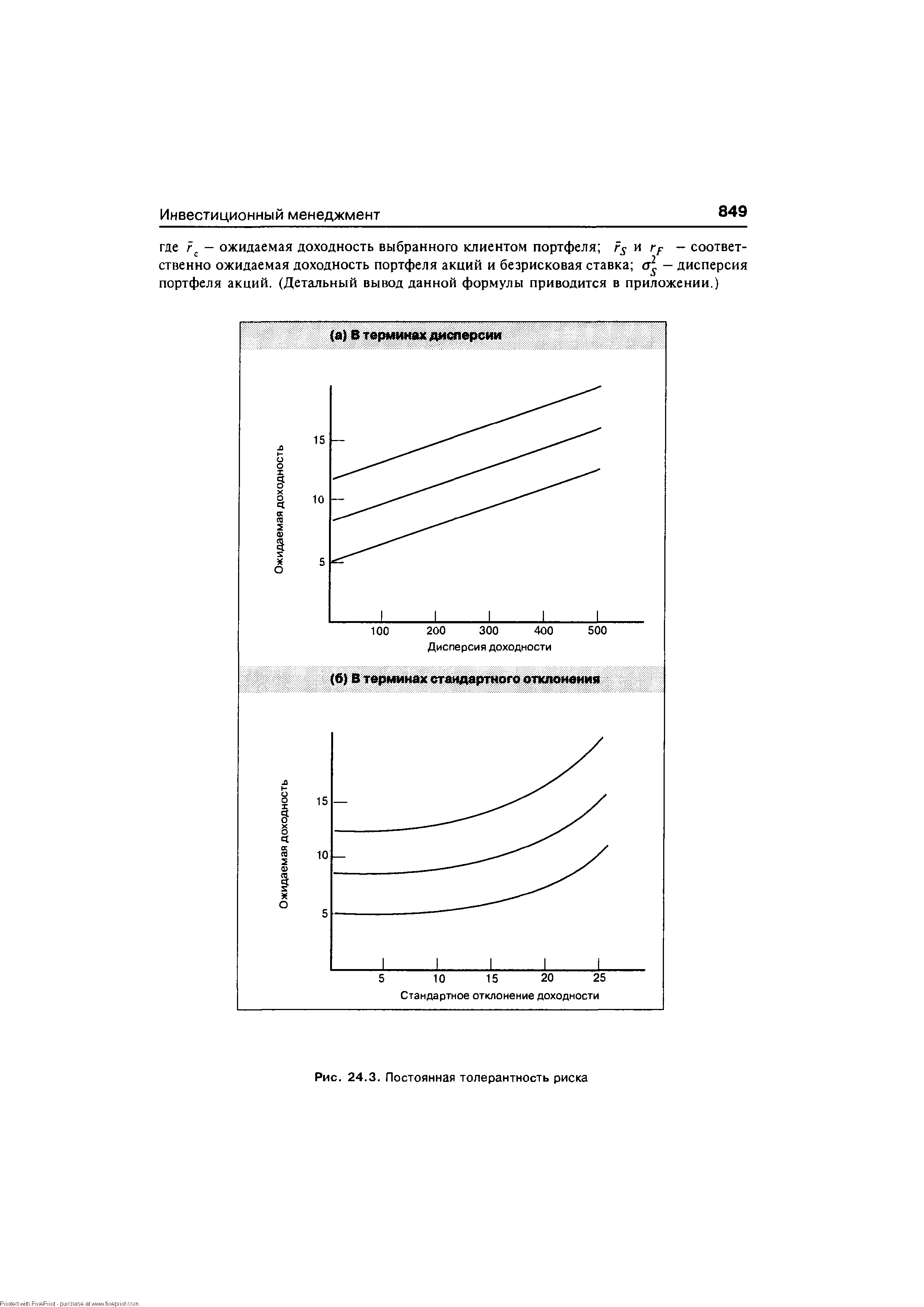 |
Постоянная толерантность риска...........................................848 [c.1026]
