По рисунку видно, что при использовании неадекватной параметрической модели погрешность наибольшая. Локальная параболическая аппроксимация с использованием полинома второй степени лучше, чем традиционно применяемая аппроксимация полиномом нулевой степени. Первая не только дает наименьшую погрешность, но и значительно устойчивее к выбору величины Ь. [c.323]
| Рис. 10.1. Зависимость погрешности локальной параболической аппроксимации от величины b для выборки объема а) п = 75 б) л = | 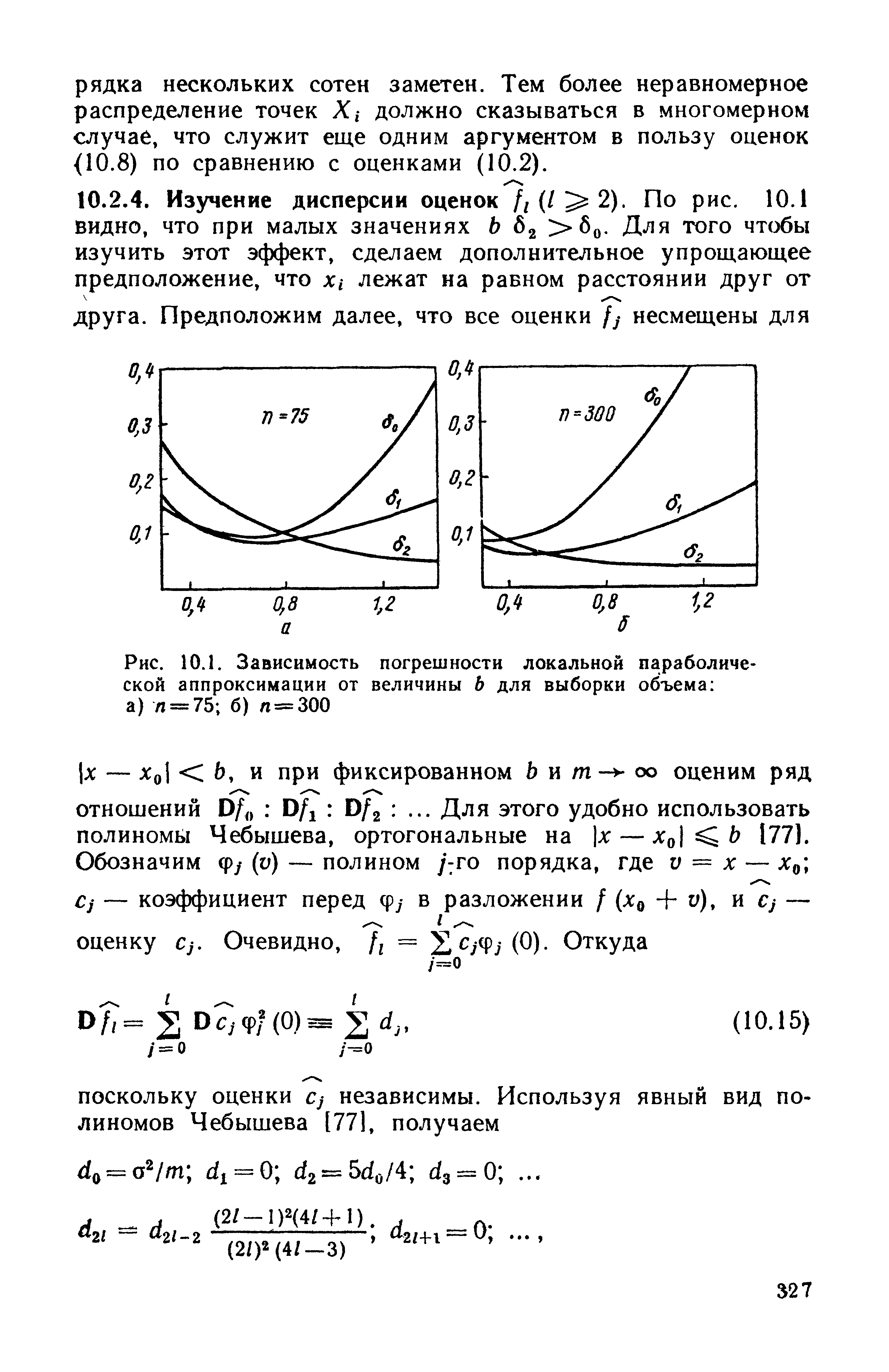 |
Алгоритм параболической аппроксимации рассчитан на достаточно гладкие функции / (х). Пусть имеется некоторая точка хй. Положим sx=a 0, s2=x°4-A, sa=x0jr2h и вычислим значения /,=/(, ), =1, 2, 3. н [c.393]
На рис. ЮЛ показаны значения 6 (/ — О, 1, 2), соответствующие непараметрическому оцениванию с помощью метода локальной параболической (порядка i) аппроксимации ( 10.2) с весовой функцией w (х, х0) = ехр — (х — х0)2/2Ь2 . Параметрическое оценивание с неадекватно предположенной моделью /пар — (а + сх) 1 в обоих случаях (п — 75 и п = 300) дало значительно большую погрешность 8пар>1. [c.323]
Смотреть страницы где упоминается термин Параболическая аппроксимация
: [c.225] [c.394] [c.475] [c.484] [c.47]Смотреть главы в:
Скоростной анализ, статические поправки, суммирование -> Параболическая аппроксимация
