Волна А может принять форму любой коррекционной модели, кроме горизонтального или наклонного треугольника. [c.74]
Теперь из коррекционных моделей нам осталось рассмотреть только наклонные треугольники. Однако перед этим просто необходимо познакомиться с некоторыми разновидностями уже известных волновых моделей, называемых сдвигающимися. [c.107]
Что касается сдвигающихся тройных троек, то такая модель на финансовых рынках вполне возможна, но здесь требуется разобраться подробнее. Вернемся к этому вопросу после знакомства с последней моделью в каталоге коррекций — наклонным треугольником. [c.113]
Из возможных взаимных положений образующих линий не был рассмотрен только вариант с наклоном их в одну и ту же сторону, но вдоль тренда старшего волнового уровня. Как раз при наклоне образующих по направлению доминирующего тренда и получаем новую волновую модель — наклонный треугольник (рис. 3-44). [c.113]
Вот начальный вариант правил для наклонных треугольников. [c.114]
Признаки наклонного треугольника. [c.114]
Наклонный треугольник всегда состоит из пяти основных волн. [c.114]
По крайней мере три волны наклонного треугольника являются зигзагами или их комбинациями. [c.114]
Образующие линии наклонного треугольника всегда направлены в одну сторону вдоль доминирующего тренда модели старшего уровня. [c.114]
Наклонный треугольник может быть предпоследней фигурой в любой модели старшего уровня. В этом случае ценовой бросок после [c.114]
Именно из такого важного свойства горизонтальных и наклонных треугольников, как их фиксированное местоположение в модели старшего уровня, и вытекают ограничения на возможный состав первых волн коррекций, указанные в признаках плоскостей, двойных троек и всех протяженных коррекций. [c.115]
На рынке FX можно встретить сходящиеся и расходящиеся наклонные треугольники, а также экземпляры с практически параллельными образующими линиями. Состав основных волн наклонных треугольников весьма традиционен для рынка FX, так как подавляющее большинство моделей состоят из одних зигзагов. Около четверти из них имеют одну волну в виде двойного зигзага. Лишь у немногих экземпляров одна волна представляет собой волновую плоскость. [c.115]
На рис. 3-45 показана редкая разновидность наклонного треугольника. Сила восходящего тренда так сдвинула его вверх, что окончание треугольника оказалось выше его начала. Таким образом, коррекционная волна [4] of iii сформировала отрицательный откат после волны [3] of iii около -3.5%. [c.115]
Ценовой бросок после наклонного треугольника (волна [5] of iii) прошел расстояние, не менее высоты треугольника (в нашем примере это высота самой широкой части треугольника между вершинами (А) и (D)). [c.115]
Кроме того, на данном рисунке пара моделей внутри наклонного треугольника представляют собой определенный интерес. Например, волна В of [c.115]
| Рисунок 3-45. Наклонный треугольник в качестве четвертой волны | 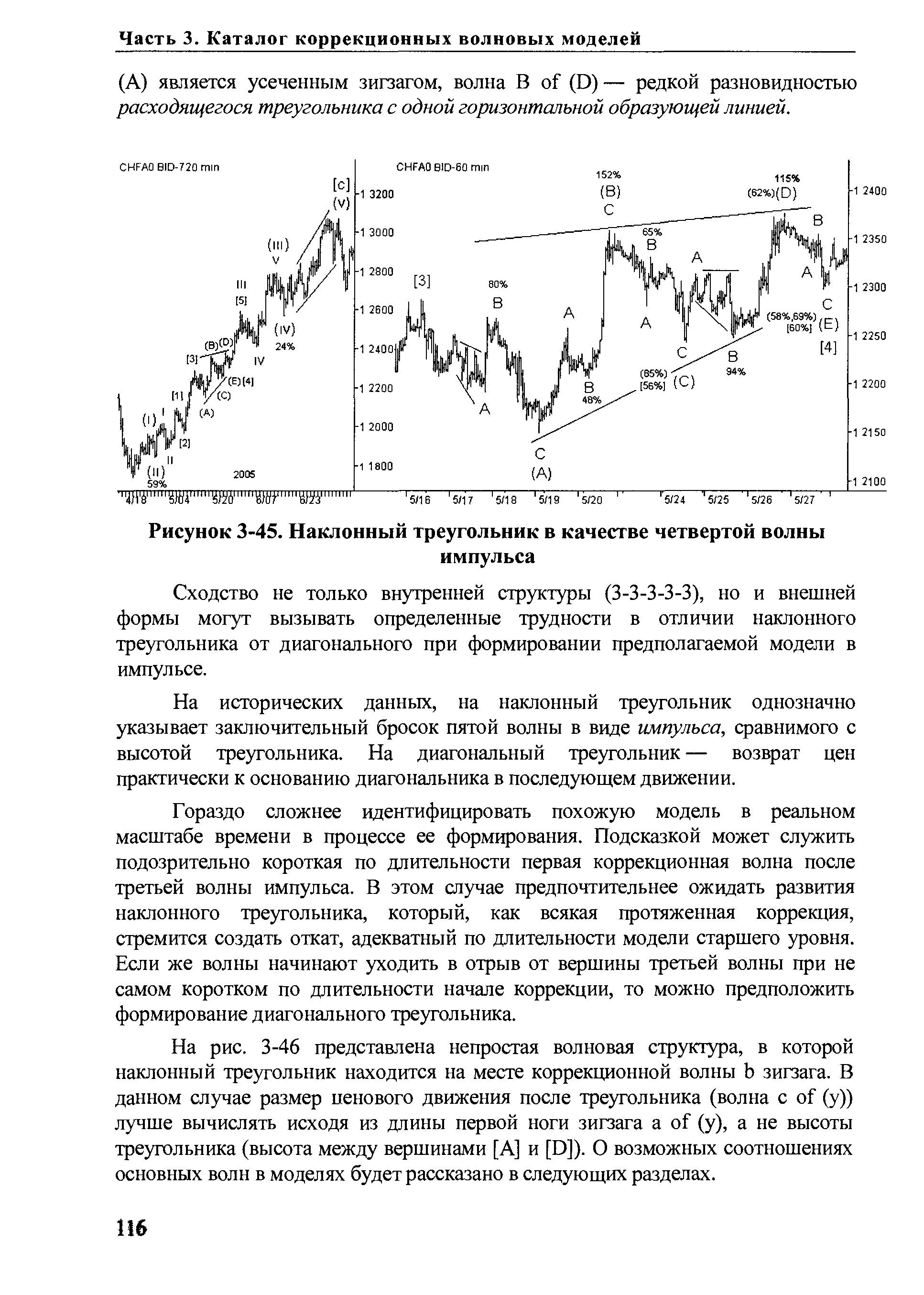 |
Гораздо сложнее идентифицировать похожую модель в реальном масштабе времени в процессе ее формирования. Подсказкой может служить подозрительно короткая по длительности первая коррекционная волна после третьей волны импульса. В этом случае предпочтительнее ожидать развития наклонного треугольника, который, как всякая протяженная коррекция, стремится создать откат, адекватный по длительности модели старшего уровня. Если же волны начинают уходить в отрыв от вершины третьей волны при не самом коротком по длительности начале коррекции, то можно предположить формирование диагонального треугольника. [c.116]
На рис. 3-46 представлена непростая волновая структура, в которой наклонный треугольник находится на месте коррекционной волны b зигзага. В данном случае размер ценового движения после треугольника (волна с of (у)) лучше вычислять исходя из длины первой ноги зигзага a of (у), а не высоты треугольника (высота между вершинами [А] и [D]). О возможных соотношениях основных волн в моделях будет рассказано в следующих разделах. [c.116]
| Рисунок 3-46. Наклонный треугольник в качестве волны b зигзага | 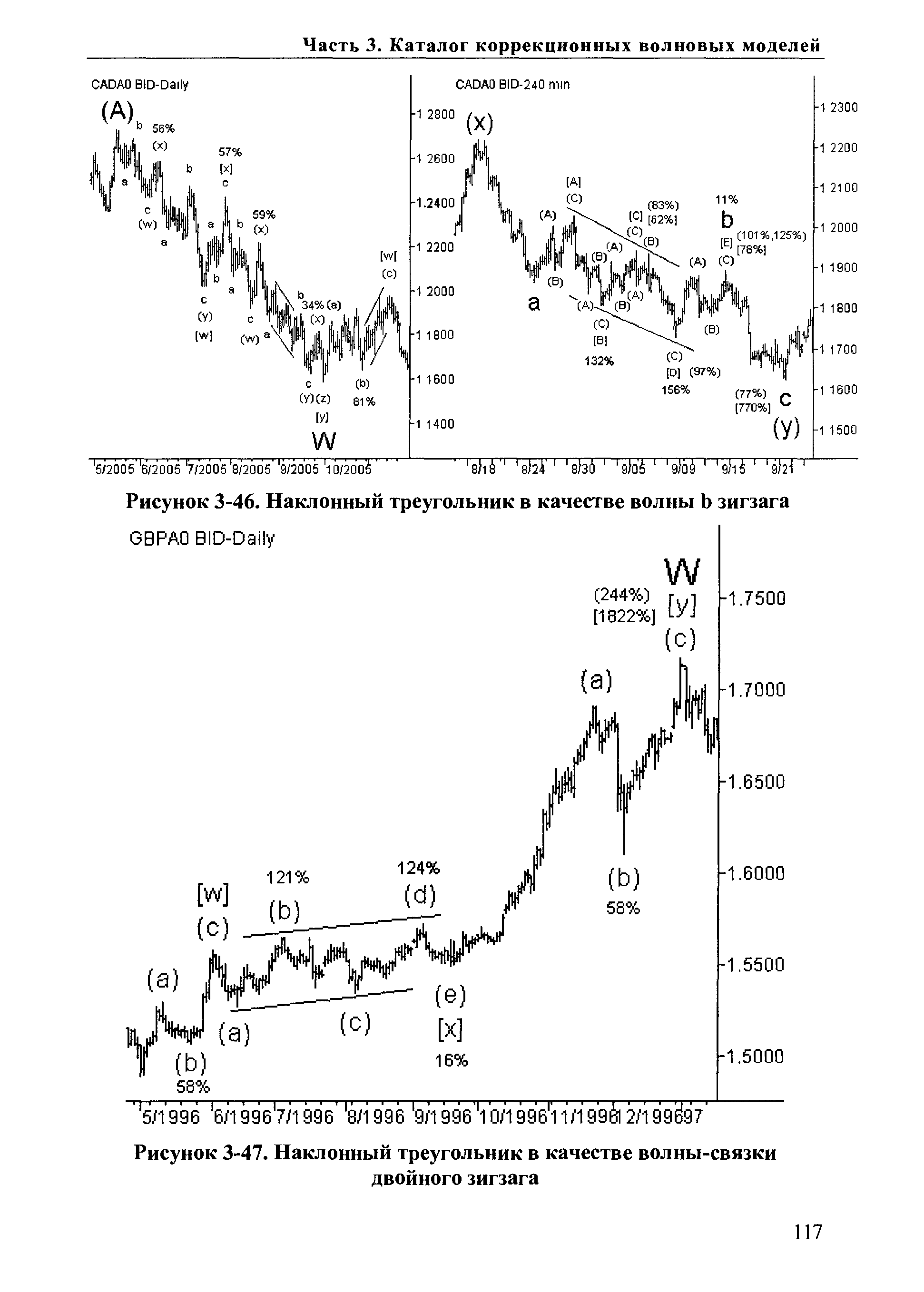 |
| Рисунок 3-47. Наклонный треугольник в качестве волны-связки | 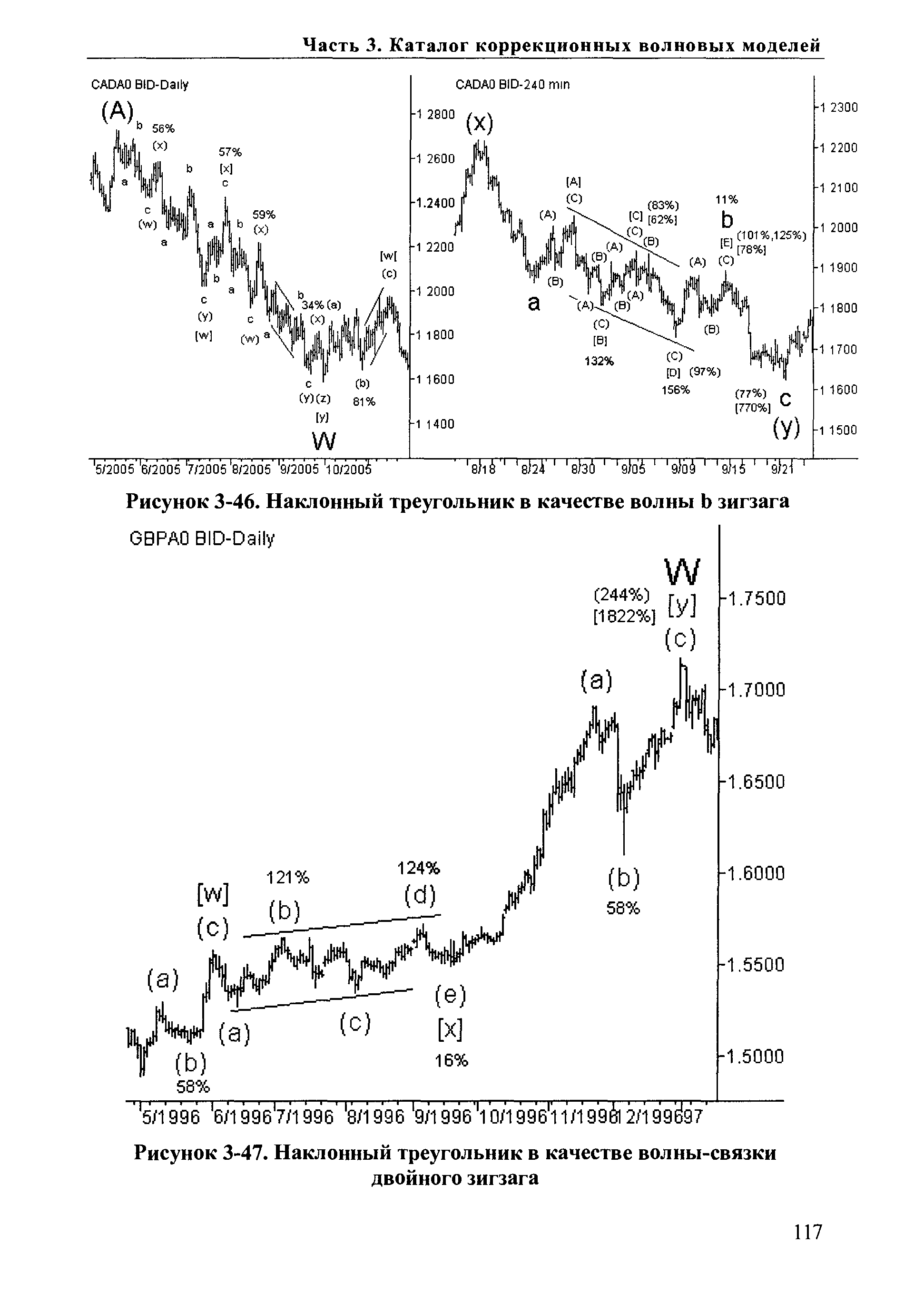 |
Пример наклонного треугольника в качестве четвертой волны диагонального треугольника в рамках основного сценария (или в качестве волны-связки XX тройного зигзага в рамках альтернативного сценария) можно посмотреть на рисунках 5-15 и 5-19. [c.118]
Примечание. Обратите внимание, что модель наклонный треугольник просто трансформируется в сдвигающуюся тройную тройку, если его последняя волна Е завершается за пределами ценовой территории волны D, то есть, если нарушается хотя бы одно правило для треугольников. [c.118]
Горизонтальный треугольник Наклонный треугольник А д к [c.124]
По наклонным треугольникам приводится собственная статистика. [c.155]
На рис. 3-47 волна [у] двойного зигзага W составила 1822% (-1794% Фибо) от его предыдущей коррекционной волны [х], или [у] = - [х] 17.94. Следует заметить, что столь большие соотношения получаются в стремительных моделях (таких, как некоторые разновидности зигзагов) с неглубокими коррекциями (особенно, с наклонными треугольниками). [c.171]
На рис. 4-35 представлен весьма интересный протяженный импульс [с] of Y ранее рассмотренного тройного зигзага (см. рисунки 4-24 и 4-25). Интересен он не только отрицательной величиной коррекции, которую сформировал наклонный треугольник [4] of hi of (iii), но и тем, что в нем не видно резкого разделения коррекций по волновым уровням. Волны именно таких конструкций допустимо [c.182]
По крайней мере, три волны наклонного треугольника являются [c.194]
На исторических данных, на наклонный треугольник однозначно указывает заключительный бросок пятой волны в виде импульса, сравнимого с высотой треугольника. На диагональный треугольник — возврат цен практически к основанию диагональника в последующем движении. [c.116]
Наверное, нет смысла говорить здесь о горизонтальных видах протяженных коррекций, так как взаимное положение их образующих линий подробно описано в соответствующем разделе. О горизонтальных и наклонных треугольниках можно сказать, что так же, как и в диагональниках заключительная волна редко завершается, коснувшись образующей линии (см. рис. 3-27 и 3-28). Чаще происходит недолет или пробитие образующей линии треугольника (см. рис. 3-29..3-47). [c.147]
Смотреть страницы где упоминается термин Наклонные треугольники
: [c.16] [c.69] [c.113] [c.114] [c.115] [c.115] [c.153] [c.193]Смотреть главы в:
Код эллиота волновой анализ рынка forex -> Наклонные треугольники
Код эллиота волновой анализ рынка forex -> Наклонные треугольники
