Расположение шикарных магазинов ограничено относительно малым пространством центральной части города, и различие в местоположении на несколько метров может привести к существенным различиям в цене. Лучшие офисные здания обычно также располагаются в форме кластеров. Определенная часть города или одна улица обычно имеет репутацию места, где протекает определенный вид деятельности, и является центром притяжения для однотипных видов деятельности. Наличие общественного транспорта и мест стоянки автомобилей увеличивает стоимость оцениваемого вида недвижимости. [c.239]
Метод кластерного анализа позволяет строить классификацию объектов посредством объединения их в группы, или кластеры, на основе критерия минимума расстояния в пространстве т показателей, описывающих объекты. Вероятностное обоснование результатов кластеризации можно получить методом дискриминантного анализа. [c.95]
Промежуточным результатом анализа являются среднее внутри-кластерное расстояние, по которому можно сравнивать различные варианты кластеризации, и кластеры с указанием включенных в них объектов. При этом можно получить проекции на плоскость каждой пары показателей центров кластеров и объектов каждого кластера, соединенных линиями с центрами. [c.96]
На рис. 9.1 приведено графическое изображение этих кластеров в координатах двух рассматриваемых показателей. [c.97]
В результате оказывается, что группировка предприятий в два кластера возможна, первый кластер включает предприятия № 3, 6, 7, 8, 9 и 10, второй — № 1, 2, 4 и 5. [c.97]
| Рис. 9.1. Изображение двух кластеров в плоскости показателей структуры балансов | 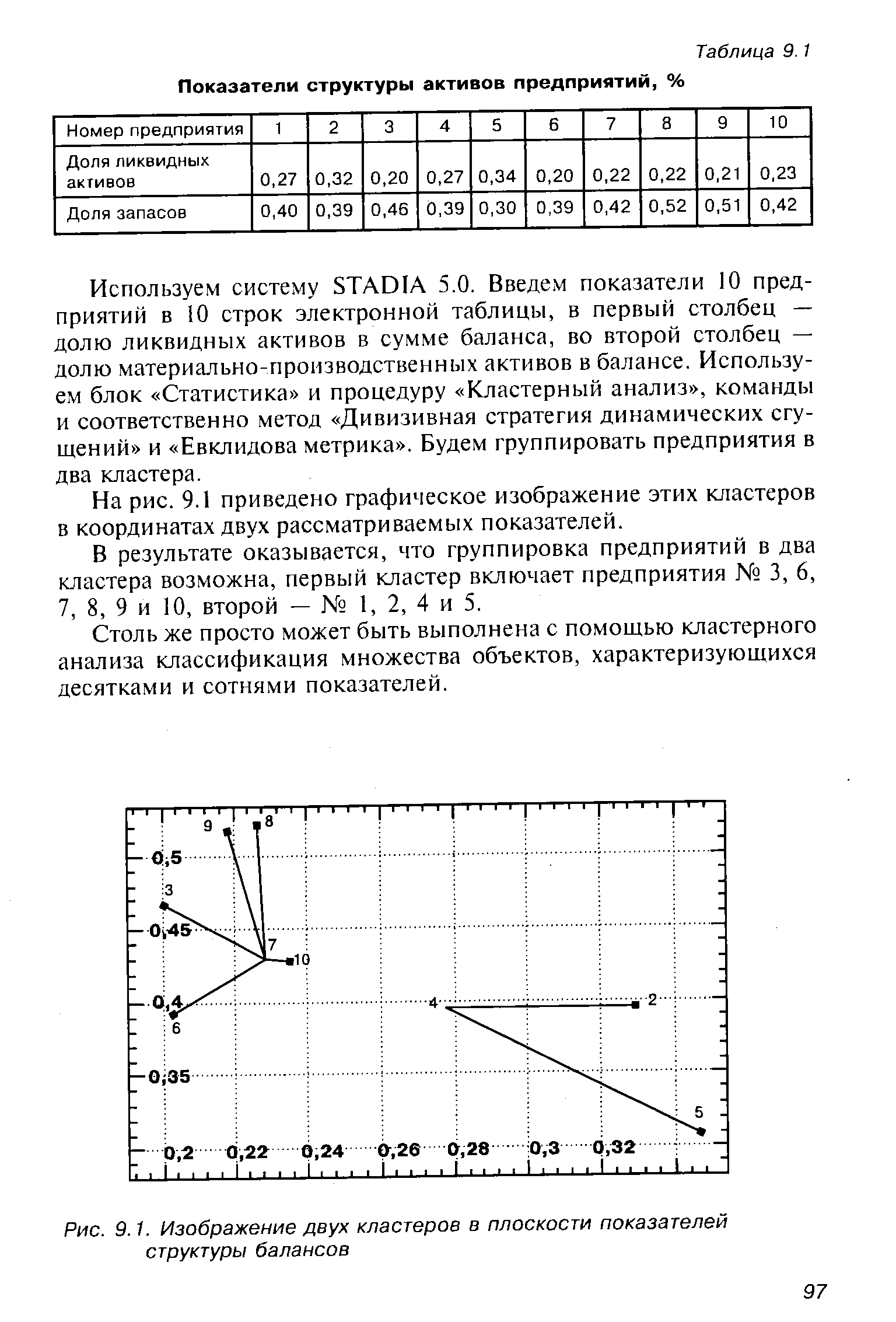 |
В нормально распределенной совокупности dчр совпадает со средним отклонением их от средней величины, т. е. нормированная разность в нормальной совокупности в среднем равна единице. Это очень важно при установлении предельного (критического) расстояния в признаковом пространстве, при достижении которого прекращается объединение кластеров. [c.138]
Заменив в- матрице евклидовых расстояний (табл. 6.13) расстояния предприятий, вошедших в первый кластер, на числа последней графы табл. 6.14, видим, что теперь минимальным является расстояние между предприятием Пригородное и первым кластером d =1,237 (табл. 6.15). [c.141]
Заменив евклидовы расстояния предприятий, вошедших в кластер, данными последней графы табл. 6.16, получим новую матрицу евклидовых расстояний (табл. 6.17). [c.141]
Средние величины по кластеру 383 98 15,9 39 0 [c.142]
Средние величины по кластеру 345 91 15,7 48 0 [c.143]
Минимальное евклидово расстояние между предприятиями Ручьи - Выборгское (оно меньше 2), следовательно, эти предприятия объединяются в кластер 2 (табл. 6.20). Кластер Б+Щ+П+А будем называть кластером 1. [c.144]
Нормированные разности и евклидовы расстояния для кластеров 1 и 2 [c.144]
Согласно табл. 6.21 все расстояния больше 2. Оставляем 4 типа предприятий предприятия, вошедшие в кластер 1, кластер 2, кластер 3 ( Всеволожское )-и кластер 4 ( Приневское ). [c.144]
Сравнивая результат кластерного анализа с многомерными средними (табл. 6.8) видим, что состав кластера 1 точно отвечает тем хозяйствам, чьи многомерные средние ниже 100%. Также выделе- [c.144]
| Таблица 6.21 Матрица евклидовых расстояний после образования кластера 2 |  |
Кластер 1 0 Кластер 2 2,770 0 Всеволожское 2,719 3,909 0 [c.145]
Перспективна возможность образования эндоэдральных комплексов фуллеренов. Радиус внутренней сферы бакибола превышает 0,5 нм, а этого достаточно, чтобы внутри разместились любые атомы и даже малые молекулы. Е)сли графит, испаряемый в лазерном луче, предварительно пропитан солью металла, то в масс-спектрах [2] образующихся углеродных кластеров появляются пики, соответствующие составу СбоМе+ (Me+=La, a, Ва, Sr, Na, К, Ni, o, Fe, s и даже U). [c.104]
Атомы металла в таких кластерах находятся внутри углеродной "клетки", поскольку для того, чтобы вырвать их "из плена", сначала необходимо разрушить углеродный скелет. Фрагментация этих ионов начинается с выщепления одной или нескольких пар атомов углерода, но не ионов металла. Здесь, вероятно, имеет место новая пространственная изомерия, вызванная "виртуальной" координацией атома металла внутри молекулы фуллерена. [c.104]
Строго говоря, атом металла будет находиться в неизвестном пока четвёртом (виртуальном) измерении, перемещаясь по внутренним натным осям х, у, z относительно внешней тривиальной системы нат X, Y, Z. Именно этот аспект фуллереновой проблемы, возможно, вызовет в скором будущем формирование нового направления в теории пространственно-структурной изомерии углеродных кластеров и, следовательно, необходимость изучения вызванных этим феноменом новых физико-химических свойств эндоэдральных соединений. [c.104]
Если внутрь фуллереновой сферы попали долгоживущие радиоактивные изотопы, то это может привести со временем к дополнительным ужасным экологическим, не существующим ранее в природе и во многом чуждым человеческому организму, последствиям. Ведь углеродные кластеры легко проходят через биологические мембраны внутрь живых клеток. Поэтому кроме непосредственного воздействия радиоактивного излучения возможно дополнительное поствременное поражение тканей живых клеток, зависящее от времени разрушения фуллеренового "сосуда" и [c.104]
Частных вариантов интеграции мояСет быть много (холдинги, финансово-строительные группы, индустриальные сети, кластеры и [c.377]
Агломеративные стратегии позволяют строить дендрограмму классификации в ходе построения иерархии объединения кластеров. Часто используют следующие варианты этой стратегии [c.96]
В результате получают матрицы расстояния между объектами, последовательности кластеров возрастающей общности с указанием входящих в кластеры объектов и расстояния между ними, на уровне которых произошло объединение кластеров, и дендрограмму — дерево объединения кластеров. [c.96]
Используем систему STADIA 5.O. Введем показатели 10 предприятий в 10 строк электронной таблицы, в первый столбец — долю ликвидных активов в сумме баланса, во второй столбец — долю материально-производственных активов в балансе. Используем блок Статистика и процедуру Кластерный анализ , команды и соответственно метод Дивизивная стратегия динамических сгущений и Евклидова метрика . Будем группировать предприятия в два кластера. [c.97]
Матрица евклидовых расстояний D служит основой агломера-тивно-иерархического метода классификации, который заключается в последовательном объединении группируемых объектов -сначала самых близких, а затем все более удаленных друг от друга. Процедура классификации состоит из последовательных шагов, на каждом из которых производится объединение двух ближайших групп объектов (кластеров). На нулевом шаге каждый [c.140]
Нормированные разности и евклидовы расстояния для кластера Бугры + Щеглово [c.141]
Следовательно, на втором шаге к первому кластеру присоединяется предприятие Пригородное . Вычисляем средние величины, нормированные разности по каждому признаку и евклидовы расстояния от кластера, включающего три предприятия ( Бугры , Щеглово , Пригородное ) до каждого из оставшихся предприятий. Результаты представлены в табл. 6.16. [c.141]
Минимальным является евклидово расстояние от кластера до предприятия Авлога . На третьем шаге образуем кластер Бугры + Щеглово + Пригородное + Авлога . Полученные средние величины для кластера, нормированные разности и евклидовы расстояния представлены в табл. 6.18, 6.19. [c.141]
Предприятия Кластер Б+Щ+П+А Ручьи Всеволож-ское Выборгское Приневское [c.144]
