Латинским квадратом А х А называется квадратная таблица из А элементов, каждый из которых встречается только по одному разу в каждой строке и в каждом столбце, например, [c.179]
На планирование по латинским квадратам накладываются следующие ограничения каждый источник неоднородности (ка- [c.179]
Чтобы использовать латинский квадрат при планировании эксперимента, нужно подвергнуть стандартный квадрат процедуре рандомизации. При этом уровни факторов определяются случайным образом для столбцов, строк, рядов и латинских букв соответственно. [c.180]
Повышение порядка латинского квадрата ведет к увеличению минимального числа уровней и позволяет сократить перебор вариантов (опытов) в несколько раз. Однако сокращение числа опытов [c.181]
Такой метод получил название латинский квадрат . Никакие другие изменения в ходе теста не допускаются. Чередование и последовательная замена факторов стимулирования позволяют исключить влияние на результаты теста различий между магазинами, особенностей клиентуры и периода продаж. Анализ сменяющихся вариантов позволяет сделать заключение о превосходстве одного варианта над другим или об их равенстве [c.146]
Если вводится третий фактор, такой, как, например, различие в инструментах, используется план эксперимента, известный под названием латинского квадрата (см. табл. 11.13). Каждый станок и каждый резец комбинируются для испытания каждого ма териала. Квадрат возникает ввиду того, что имеется три переменных фактора (станки, инструмент и материал) и число возможных состояний для каждого фактора одинаково. Значимость трех источников вариации можно определить с помощью методов дне- [c.191]
| Таблица 11.13 Латинский квадрат | 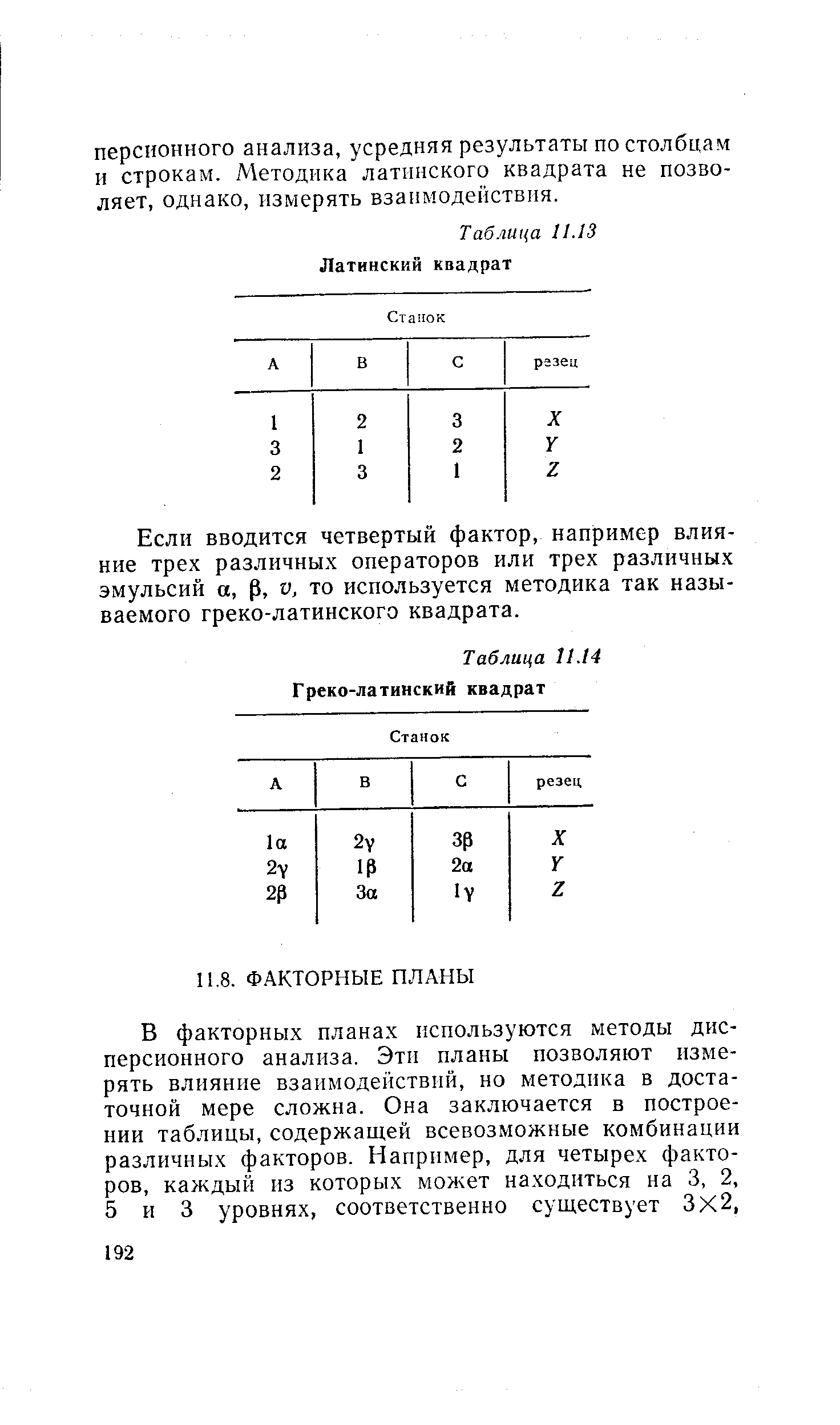 |
Как показывает в большинстве случаев маркетинговых исследований посторонние факторы, такие как объем продаж, размер магазина, тип магазина, его род занятий и статус респондентов, влияют на значения зависимых переменных. Таким образом, модель случайных групп употребляется чаще, чем модели, основанные на случайном отборе респондентов. Однако основным недостатком этой модели является то, что исследователь с ее помощью может в каждом отдельном случае контролировать только один посторонний фактор. Б ситуациях, когда необходимо контролировать несколько посторонних факторов одновременно, используются модель Латинского квадрата или модели. [c.294]
Модель латинского квадрата [c.294]
I. Таблица 7.5. Пример применения модели латинского квадрата [c.294]
Хотя модель латинского квадрата весьма популярна в маркетинговых она все же не свободна от Ее применение выделения одинакового количества категорий респондентов по обоим контролируемым посторонним факторам и такого же количества значений базисного фактора, что иногда проблематично. Примечательно, что в приведенном примере потребовалось объединить покупателей, редко совершающих покупки в универмаге, и не являющихся покупателями универмага, категорию для того, чтобы применение модели латинского квадрата стало возможным. Кроме можно контролировать одновременно только два посторонних фактора. Контроль большего количества посторонних факторов возможен при применении одного из вариантов этой модели, модели латинского квадрата- Кроме того, мод ель латинского квадрата не позволяет определить характер взаимодействия посторонних факторов между собой или с независимым фактором. Для анализа взаимодействий такого рода необходимо использовать факторные модели. [c.294]
Для иллюстрации применения модели латинского квадрата допустим, что в описанном примере в дополнение к постороннему фактору частоты совершения покупок в данном универмаге необходимо контролировать еще и посторонний фактор степени заинтересованности в информации о данном универмаге, для которого установлены такие категории средняя и низкая. Чтобы применить модель латинского квадрата, придется также объединить покупателей, совершающих покупки в универмаге изредка, с теми, кто никогда не совершает здесь покупок, в одну категорию. Выбор рекламных роликов для демонстрации группе респондентов в каждой ячейке сделан так, как показано в табл. 7.5. Примечательно, что каждый из рекламных роликов А, В и С появляется в каждой строке и в каждой таблицы только один раз. [c.295]
Назовите недостатки модели латинского квадрата. [c.310]
Можно еще дальше усовершенствовать эксперимент, связанный с определением урожайности культуры и зависимый от качества обработки почвы. Если каждого рабочего закрепить за определенным полем, то вследствие различности почв может появиться систематическая ошибка. Обозначим поля буквами W, X, У, ZH определим условия эксперимента рабочих между полями таким образом, чтобы каждый из них обслуживал поле только один день. В этом случае получим план, называемый греко-латинским квадратом, который позволяет усреднить влияние таких факторов, как день, поле, рабочий (табл. 4.6). [c.160]
Способ восстановления — операция, обратная расщеплению , — замена плана с факторами на малом числе уровней планом с одним из факторов х ", на большем числе уровней (в табл. 4.17 показано обратной стрелкой). При планировании экспериментов и наличии качественных факторов, когда все или их часть являются качественными (сортность вещества, его качество и т.д.), целесообразно применение неполно-блочных планов, т.е. таких планов, которые разрабатываются на основе полнофакторного эксперимента, но с существенным уменьшением числа экспериментов. К таким планам относятся латинские квадраты и кубы. [c.179]
Комбинация двух ортогональных квадратов носит название латинского квадрата второго порядка. Если элементы первого квадрата обозначаются латинскими буквами, а второго — греческими, то такой квадрат называется греко-латинским, например, [c.180]
Каждый элемент внутри греко-латинского квадрата встречается только один раз по строке и по столбцу (табл. 4.18). [c.180]
Условия опытов внутри греко-латинского квадрата [c.181]
Каждый греко-латинский квадрат — это 1/Л2 реплики от полного факторного эксперимента (ПФЭ) [c.181]
Для четырех факторов на Л - 3 величина Апфэ = 3" = 81. В этом случае план на основе греко-римского квадрата позволяет оценивать значимость факторов с помощью только девяти опытов. Три ортогональных квадрата образуют латинский квадрат третьего порядка, или гипер-греко-латинский квадрат (соответствует 1/й3 реплике от ПФЭ). [c.181]
Латинские кубы. На основе латинских квадратов можно построить и другие планы различной мощности. Латинский куб hxhxh первого порядка — это кубическая таблица из h элементов, расположенных на Л3 позициях таким образом, что каждый элемент входит в эту таблицу А2 раз и встречается в каждой из плоскостей (в каждом сечении таблицы) одинаковое число раз, равное h (h — число уровней факторов). Латинский куб представляет собой h сбалансированных квадратов раз- мером h x h, причем каждый квадрат (или блок) поставлен в соответ-Ъвии с уровнем четвертого фактора. [c.182]
Если вводится четвертый фактор, например влияние трех различных операторов или трех различных эмульсий а, р, v, то используется методика так называемого греко-латинского квадрата. [c.192]
| Таблица 11.14 Греко-латинский квадрат | 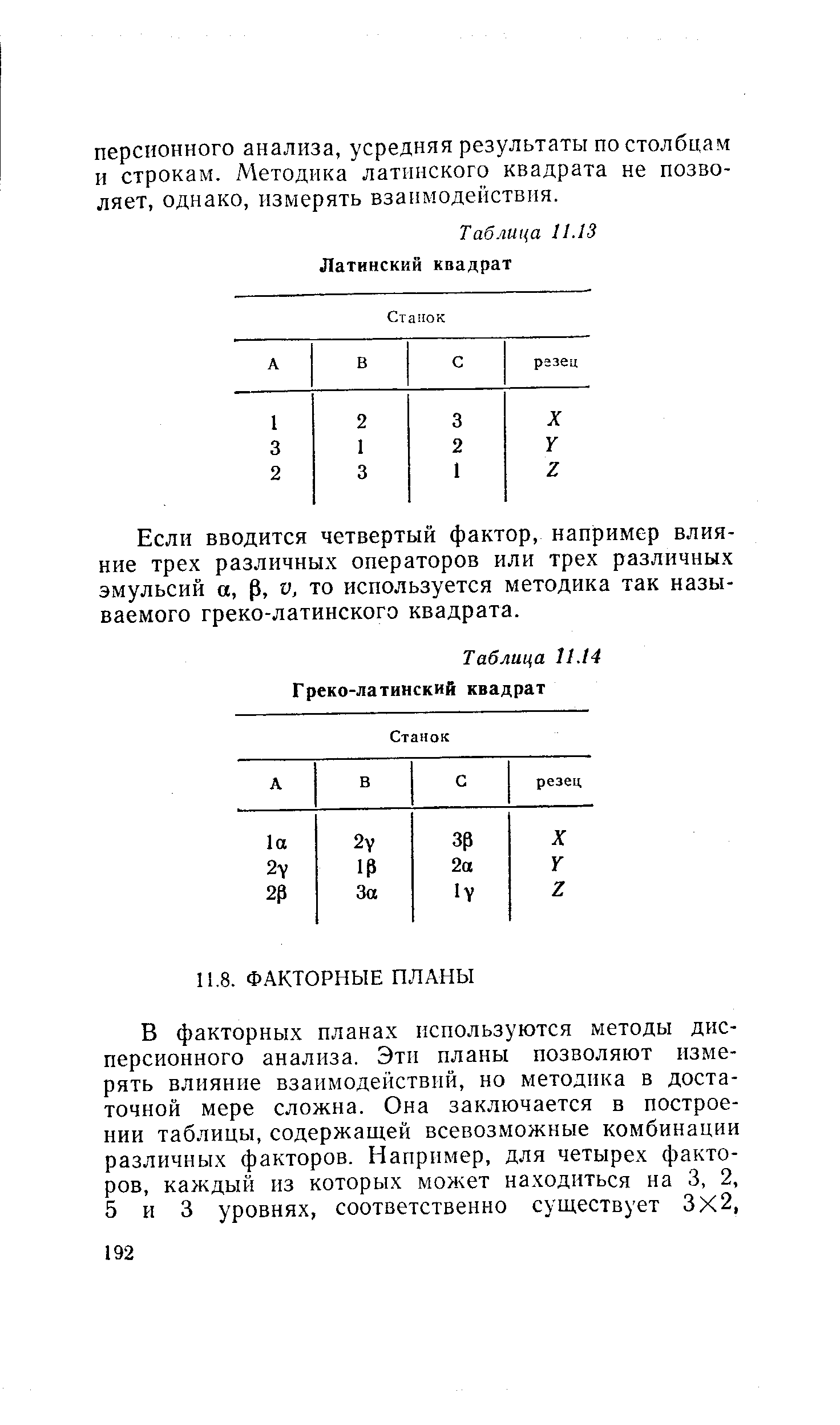 |
