Совокупный риск суммы доходов, например хозяйственного портфеля предприятия или портфеля ценных бумаг, можно оценить на основе данных о величине йота-коэффициента по каждому источнику дохода и данных о корреляции поступлений доходов из этих источников, рассчитав йота-коэффициент. Математическое ожидание общего дохода определяется как сумма математических ожиданий доходов из каждого источника. Дисперсия общего дохода определяется как [c.121]
Риск чистой текущей стоимости является основной мерой риска долгосрочных инвестиций. Его оценка ведется путем исчисления величины йота-коэффициента чистой текущей стоимости. Ожидаемую чистую текущую стоимость определяют по формуле 12.2. Для [c.134]
Величину йота-коэффициента чистой текущей стоимости рассчитывают следующим образом. Определяют дисперсию чистой текущей стоимости [c.135]
Тогда йота-коэффициент ожидаемой величины чистой текущей стоимости определится из выражения [c.135]
Если йота-коэффициенты денежных потоков известны, то йота-коэффициенты текущей денежной стоимости потока в /-м году при заданной ставке дисконтирования определятся равенством [c.135]
Величина йота-коэффициента текущей денежной стоимости проекта определится из выражения [c.135]
Определяем йота-коэффициент текущей стоимости денежного потока в первом году по формуле 12.14 (1РУ)2 — 0,202 х 1 + [1 х х 0,30/(1 + 0,30)]2 х (0,20/0,20)2 = 0,04213. Определяем йота-коэффициент текущей стоимости денежного потока во втором году по формуле 12.14 (7т)2 = 0,202 х ] + [2 х 0,30/0 + 0,30)]2 х х (0,20/0,20)2 = 0,04852. Определяем величину йота-коэффициента текущей стоимости проекта по формуле 12.12 (Ipv)2 = [(0,04213 х [c.136]
В настоящем разделе йота-коэффициент предложен в качестве метода, позволяющего аналитику лучше оценить надежность прогнозов фирмы в отношении поступления средств от операций. В нем рассмотрена идея выявления изменчивости потоков средств от операций по годам в отдельных отраслях. Оценив эти колебания, аналитик может применить риски, установленные для отрасли, к каждому конкретному прогнозу фирмы в отношении потоков средств. [c.411]
Определение йота-коэффициента [c.412]
| Таблица 9.6. Пример 1-й расчета йота-коэффициента | 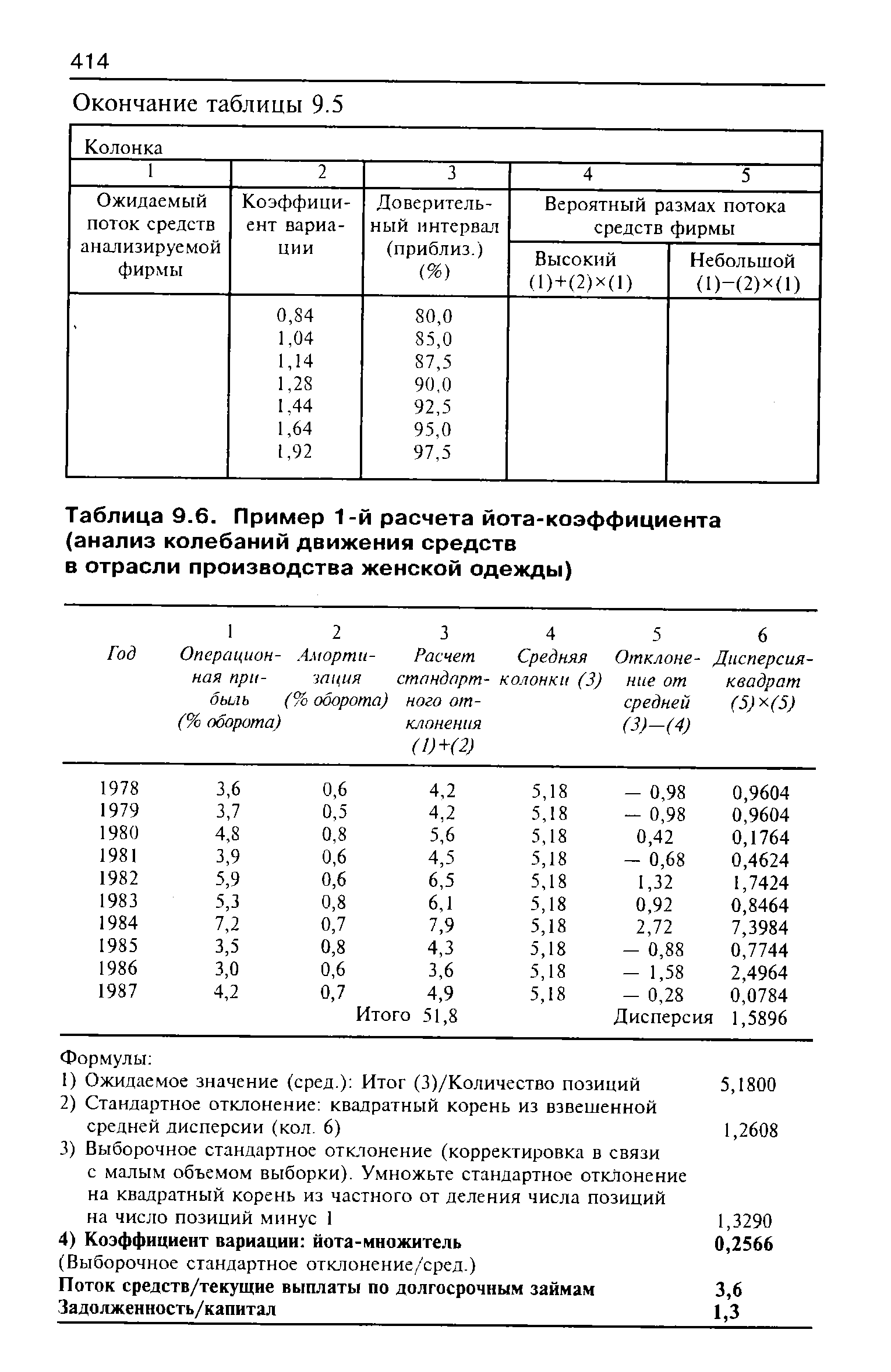 |
Предварительное обоснование йота-коэффициента [c.416]
Представляет интерес сопоставление йота-коэффициента с имеющимися распространенными показателями. В основе этого сопоставления лежит гипотеза эффективного рынка. Иначе говоря, если отрасль получала надлежащие кредиты, с учетом степени присущего ей риска, должно оказаться, что коэффициент "задолженность/капитал" в отрасли женской одежды ниже, чем в отрасли грузовых перевозок, где изменчивость меньше. Из табл. 9.8 видно, что эта гипотеза справедлива. В среднем за 1981—1987 гг. коэффициенты "прибыль/процентные расходы" и "наличность/ [c.416]
| Таблица 9.7. Пример 2-й расчета йота-коэффициента |  |
| Таблица 9.8. Сопоставление йота-коэффициента с распространенными показателями |  |
Коэффициент вариации — йота-коэффициент как измеритель риска. Как правило, чем выше ожидаемая доходность, тем больше величина его среднего квадратического отклонения. Но в общем случае и величины доходности, и колеблемость, т.е. изменчивость доходности, могут быть различными. Поэтому для оценки меры относительного риска при различной ожидаемой доходности рассчитывают риск, приходящийся на единицу доходности, путем определения коэффициента вариации. Этот коэффициент, который часто называют йота-коэффициентом, представляет собой отношение среднего квадратического отклонения к ожидаемому значению доходности [c.60]
Пример. Оценим относительный риск проектов, показатели которых приведены в табл. 3.1. Используя данные о величинах ожидаемой доходности и ее среднеквадратическом отклонении, вычисленные ранее, по (3.4) подсчитываем йота-коэффициент для первого [c.60]
Используя формулы (3.3) и (3.4), можно будет вычислить средние квадратические отклонения и йота-коэффициенты. [c.61]
Портфель, состоящий из множества активов. При добавлении в портфель все большего количества новых активов, как правило, риск портфеля будет быстро снижаться. Характеризовать риск портфеля, составленного из множества активов, можно с помощью I-коэффициента (йота-коэффициента), который, как было указано, представляет собой отношение среднеквадратического отклонения и ожидаемой доходности и определяется в этом случае [c.67]
Из выражения 11.8 можно получить формулу для оценки величины йота-коэффициента суммарного дохода из многих равноценных источников1 [c.122]
Нестабильность ставки дисконтирования возникает в условиях колебания учетных ставок, ставок процентов по кредитам, ставок рефинансирования Центрального банка. Эта нестабильность может быть охарактеризована величиной йота-коэффициента. При нестабильной ставке дисконтирования йота-коэффициент текущей стоимости денежного потока в /-м году можно определять из выражения1 [c.136]
При корреляции стоимостных оценок денежного потока и ставки дисконтирования, которая охарактеризуется коэффициентами корреляции, формулы 12.7,12.8, 12.10—12.14 не применяются. С учетом этой корреляционной связи йота-коэффициент текущей стоимости денежного потока в / -м году определяется выражением [c.137]
Пример — продолжение предыдущего примера. Оценим риск проекта с учетом того, что между стоимостной оценкой денежного потока и ставкой дисконтирования есть корреляционная, коэффициент корреляции отрицателен и составляет — 0,2. Определяем йота-коэффициент текущей денежной стоимости потока в первом году по формуле 12.15 (/т)2 = 0,202 х 1 + [1 х х 0,30/(1 + 0,30)]2 х (0,20/0,20)2- 2 х (- 0,2) х [1 х 0,3/0 + 0,3)]х х (0,2/0,2) = 0,0458. Определяем йота-коэффициент текущей стоимости денежного потока во втором году по формуле 12.15 (/т)2 = = 0,202х 1 + [2 х 0,30/0 + 0,30)]2 х (0,20/0,20)2 - 2 х (-0,2) х х [2 х о.З/О + 0,3)] х (0,2/0,2) = 0,06329. Определяем величину йота-коэффициента текущей денежной стоимости проекта по формуле 12.12 (Гру) = [(0,0458 х 92 + 0,06329 х 92]/182 = 0,02727. [c.137]
Формулы (3.5) и (3.6) используются для анализа выборочных данных, а исходные данньге рассматриваются как выборка из более крупной совокупности. Использование временных рядов для прогнозирования основывается на предпосылке, что существующие тенденции сохранятся и в будущем. В этом случае временные ряды можно использовать как основу для составления прогнозов, а полученные средние значения доходности, дисперсии, среднего квадратического отклонения и йота-коэффициентов — для оценки акций, облигаций, других финансовых инструментов, инвестиционных проектов, производимых и реализуемых товаров и услуг, предприятия в целом. [c.61]
Смотреть страницы где упоминается термин Йота-коэффициент
: [c.120] [c.120] [c.122] [c.122] [c.135] [c.135] [c.135] [c.136] [c.136] [c.136] [c.136] [c.137] [c.137] [c.137] [c.411] [c.412] [c.420] [c.60] [c.68] [c.68]Смотреть главы в:
Анализ финансовых отчетов (на основе GAAP) -> Йота-коэффициент
