| Рис. 1. Геометрическая интерпретация дифференциала | 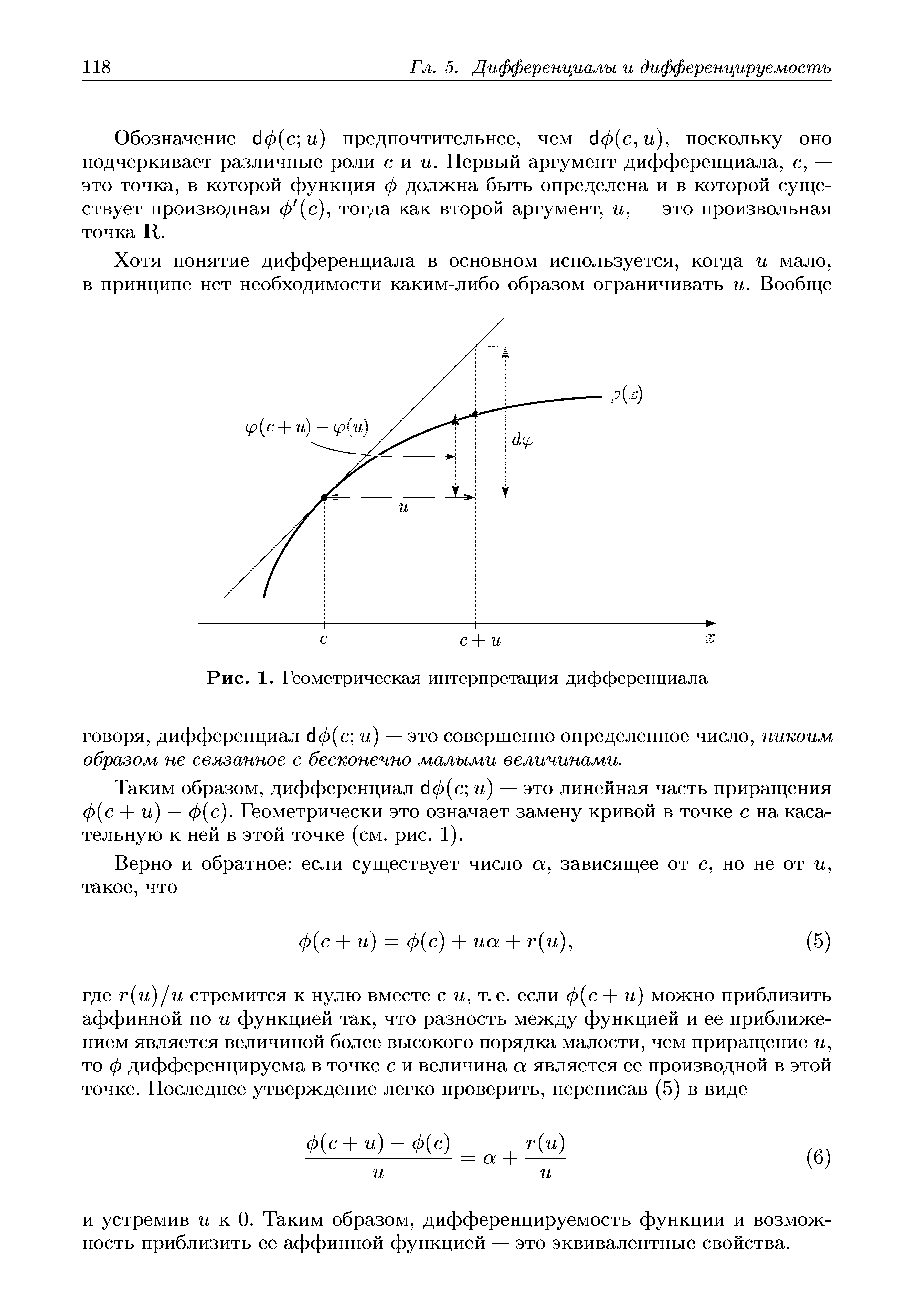 |
Определение и геометрический смысл дифференциала 103 5.2 2. Приближенные вычисления с помощью дифференциала 1 4 [c.5]
Определение и геометрический смысл дифференциала [c.103]
Геометрический смысл дифференциала. Пусть у = Дх) - дифференцируемая в точке х0 функция, график которой изображен на рис. 3.4а, МйТ- касательная к графику функции у = Дх) в точке Af0 с абсциссой Хд. Рассмотрим ординату этой касательной, соответствующую абсциссе х + Дх. Из прямоугольного треугольника ДАО/Т находим NT= A Mga, но M0N= Дх и tga = /(х.). Поэтому NT = /(х0)Дх = df xj. Таким образом, дифференциал функции у = Дх) в точке х0 равен приращению ординаты касательной, проведенной к графику этой функции в точке (х0 Дх0)), соответствующему приращению ее абсциссы х0 на Дх. Можно показать, что этот вывод не зависит от расположения графика функции и касательной на координатной плоскости (см. рис. 3.46). [c.55]
