Реализация цели или плана, в соответствии с этим графом, начинается с задач (т—1—п)-то ранга или уровня и далее вверх до достижения главной цели. Эти положения в одинаковой мере справедливы как к функционирующей системе, так и к процессу их сооружения. Объясняется это тем, что как процесс функционирования системы, так и ее развитие представляется последовательной сменой состояний. В первом случае изменяются существенные переменные параметры при постоянной структуре системы, а во втором — изменяется во времени еще и структура системы. [c.37]
Потребители проставляют во 2-й графе опросного листа ранги, которые они присвоили отдельным свойствам товара, а в одной из последующих граф отмечают условным знаком (например, крестом) свое согласие с той или иной оценкой каждого свойства. Это дает возможность после обработки всех опросных листов определить единичные уровни качества товара по любому свойству, независимо от того, выражена оценка численно или словесно. Каждый из пяти градаций оценки свойства присваивается естественный порядок отлично —1, хорошо — 2, средне - 3, удовлетворительно — 4, неудовлетворительно — 5. Средние порядковые оценки свойств, данные потребителями, преобразуются в единичные уровни качества по формуле [c.63]
Коэффициенты значимости при К, определяются на основе усредненных рангов. Информация для их расчета содержится во 2-й графе опросного листа. Расчет проводится в предположении линейной зависимости значимости по известной формуле [c.64]
Если располагают нормативными значениями показателей, утвержденных финансовыми органами и органами страхового надзора, то тогда за оптимальное принимается рекомендуемое значение. Далее производится ранжирование абсолютных значений отклонений индивидуальных значений коэффициентов от рекомендованного. Например, оптимальным является портфель, перестрахованный на 45%. В этом случае ранг будет определяться в соответствии с абсолютным значением отклонений значений коэффициента от 0,45 Х,-0,45 . В нашем примере абсолютные значения отклонений представлены в графе 8-А табл. 10.4, а присвоенные ранги указаны в графе 8-Б. Показатель доли управленческих расходов необходимо минимизировать, поэтому с рядом оговорок можно считать, что чем меньше значение этого показателя, тем ранг выше. В графе 9 минимальное значение коэффициента равно 0,08, следовательно, ему присваивается первый ранг и т.п. [c.426]
Раньше была проблема поиска соответствия между иерархиями и властями разных стран. Например, кто был выше, граф в России или курфюрст в Германии В старой требовались всевозможные табели о рангах. В новой иерархии этот вопрос решается просто пересчётом денежного состояния согласно курсу валюты. Иерархия или отдельный человек любой страны автоматически включаются во всемирную иерархию. Регулировать относительную власть местных иерархий можно простым изменением курса валют. [c.78]
Проанализируйте факторы, определяющие отношение к труду, по степени их значимости для Вас в настоящее время. Рангом 1 обозначьте самый важный для Вас фактор в графе Ранг значимых факторов , а фактор, вызывающий самое большое Ваше недовольство, в графе Ранг факторов неудовлетворенности . Один и тот же фактор может рассматриваться и как значимый, привлекающий, и как вызывающий неудовольствие, если он использован недостаточно. [c.370]
| Рис. 5. Граф целей и операций сложной системы п — ранг цели т — операция | 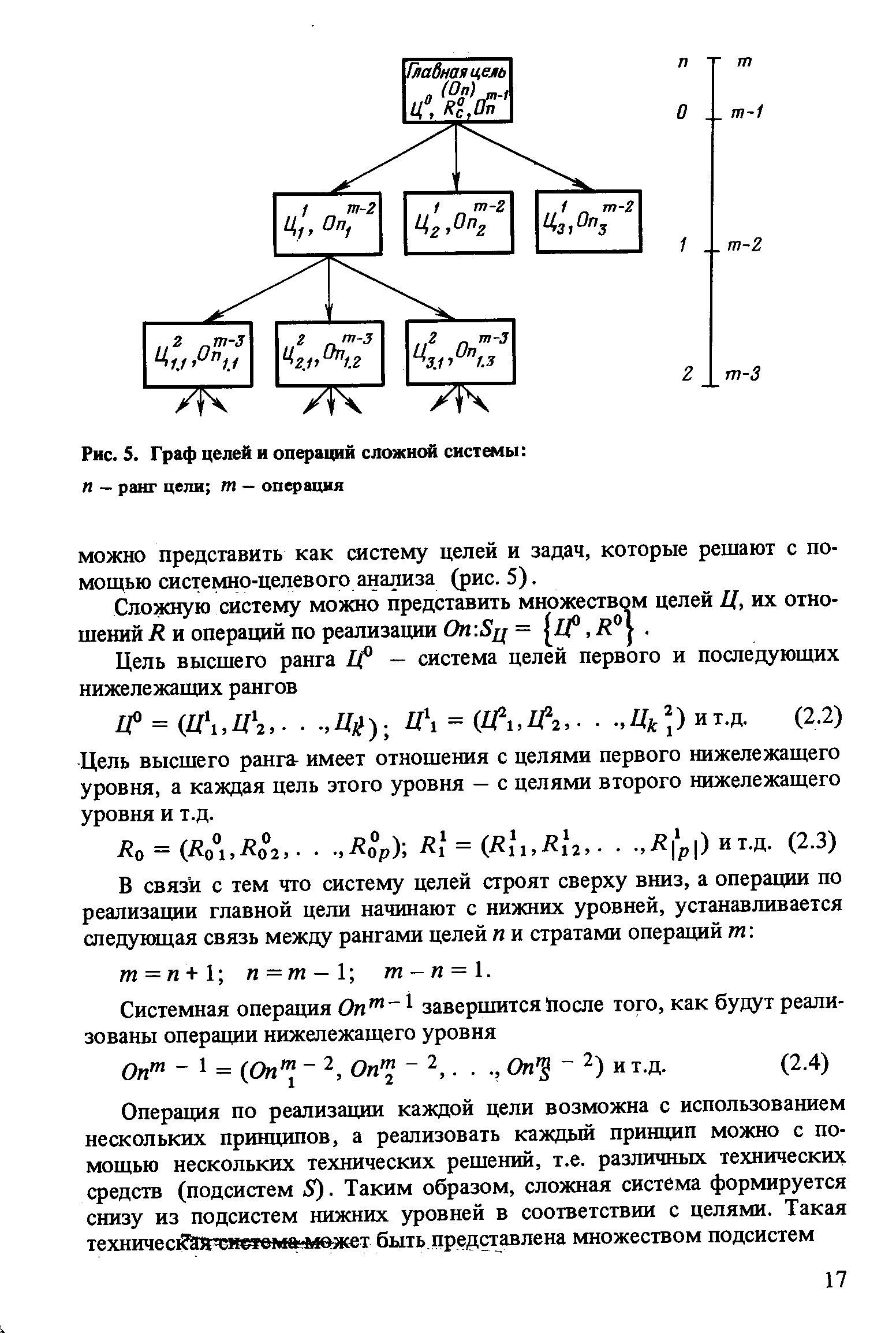 |
Принцип присвоения рангов поясним на примере. В заявке № 3 на оборудование ранг каждой позиции записан во второй графе. [c.58]
Графа 2 содержит специальный признак, по которому определяется оборудование, требующее монтажа. Если в этой графе записаны 1 или 2 (что соответствует рангу данной позиции), то это означает, что данная позиция требует затрат на монтаж, и эти затраты должны учитываться при определении общей стоимости оборудования, требующего монтажа. Если в этой графе записан нуль, то это означает, что данная позиция либо не требует затрат на монтаж, либо является позицией 1-го ранга, требующей монтажа, но она расшифровывается позициями 2-го ранга, которые будут учитываться при определении общей стоимости оборудования, требующего монтажа. [c.132]
Из табл. 5.18 следует, что располагаемые ресурсы в 13 000 ч машинного времени позволяют включить в формируемый набор задачи первых шести рангов, которые обеспечены не только вычислительными, но и трудовыми ресурсами. При располагаемых трудовых ресурсах в 6590 чел.-ч этот набор требует трудовых ресурсов 6385 чел.-ч (табл. 5.18). Очевидно, в дальнейшем формировании набора задач по оцениваемой ветви нет необходимости. Составленный набор задач по этой ветви, как это видно из табл. 5.17 и 5.18, совпадает с их набором, составленным при оценке первой ветви графа. Естественно, совпадает и годовая экономия, подсчитанная для такого набора задач в той и другой таблицах. Эта экономия равна 102700 руб. [c.186]
Из табл. 5.20 следует, что располагаемые вычислительные ресурсы в объеме 13 000 ч в полной мере обеспечивают набор задач первых шести рангов с годовой экономией в 99 200 руб. Поскольку получаемая экономия меньше экономии базового набора задач, сформированного по ветви К->-П->-Т- -В, то дальнейшее формирование наборов задач по ветви К- -В->П- -Т прекращаем, так как два оставшихся возможных набора заведомо обеспечивают меньшую годовую экономию. Не формируем их и по ветви К->-В- -Т->-П, так как вторым ее элементом является тот же набор задач В. На этом формирование и оценку наборов задач первого фрагмента графа завершаем и приступаем к формированию и оценке наборов задач второго фрагмента графа (рис. 5.4). [c.188]
Расчеты также показывают, что задачи первых 9 рангов обеспечивают годовую экономию в 110 250 руб. Поскольку получаемая экономия превышает экономию базового варианта в 102 700 руб., то дальнейший отбор задач для описываемого фрагмента графа необходим. [c.190]
Из тех же расчетов следует, что задачи первых 9 рангов требуют 246 180 руб. капитальных вложений. Поскольку предприятие располагает ресурсами по капитальным вложениям на сумму 298 000 руб., то сформированный набор в 9 задач оказывается обеспеченным не только предпроизводственными, но и капитальными ресурсами. Разумеется, составляемые на более нижних (втором, третьем и четвертом) уровнях наборы задач заведомо будут обеспечены капитальными ресурсами, так как они формируются из набора задач первого уровня, уже обеспеченного располагаемыми капитальными ресурсами. Поэтому исходный второй фрагмент графа, приведенный на рис. 5.4, упрощается и в него войдут лишь две ветви П->-Т->В и n-+B-Vr. [c.190]
Формируем теперь набор задач по ветви Т- -В->П уточненного графа. Для этого ранее составленный набор из 10 задач по критерию эффективности пред-производственных затрат ранжируем по критерию эффективности затрат машинного времени. Результаты такого ранжирования приведены в табл. 5.24. Из этой таблицы следует, что в формируемый набор должны быть включены задачи первых семи рангов, обеспечивающие годовую экономию в 100200 руб. Эта экономия также меньше экономии в 102 700 руб. базового варианта. Поэтому рассматриваемый набор оказывается неконкурентоспособным. Прекращаем и дальнейшее составление набора задач по этой ветви графа, т. е. на этом заканчиваем формирование и оценку наборов по третьему фрагменту графа. [c.194]
Из табл. 5.25 следует, что при заданных вычислительных ресурсах в 13 000 ч машинного времени в формируемый набор должны быть включены задачи первых семи рангов, так как лишь они обеспечены вычислительными ресурсами. Набор из семи задач обеспечивает годовую экономию в 108200 руб., которая больше экономии в 102 700 руб. базового набора. Поэтому необходимость дальнейшего перебора и оценки других наборов задач анализируемого четвертого фрагмента графа не отпадает. [c.197]
Как уже отмечалось, классификация адаптивных свойств в целом представляет собой древовидный ориентированный граф. Каждая из вершин этого графа представляет адаптивное свойство того или иного уровня в классификационной иерархии, корень графа — полное множество адаптивных свойств АСУ. Множество дуг графа является отображением разбиения отдельных подмножеств адаптивных свойств на подмножества адаптивных свойств иерархически более низкого уровня (ранга) или элементарные адаптивные свойства, т. е. такие, которые не являются совокупностью двух или более других адаптивных свойств. Отметим, что ранг элементарных адаптивных свойств равен 1. [c.33]
Помимо названных методов экспертных оценок, как научного инструмента решения экономических задач, в условиях неопределенности и риска могут найти применение метод ранга, метод прогнозного графа, метод комиссий и др. [c.62]
В графах 3-6 представлены соответственно количественные значения соответствующих параметров, значение ранга каждого параметра, значение ранга, скорректированного на показатель важности параметра для покупателя. Например, возьмем параметр мощности. В графе 3 279 л. с. — величина мощности, 3 — значение ранга мощности, 0,9 — ранг мощности, скорректированный на показатель важности мощности для покупателя (/-.) (0,9 = 0,3 х 3). [c.393]
В нем укажем данные 2-й графы табл. 3 (вместе с заголовком), относящиеся к фирме Колокольный звон (это диапазон ячеек В 1 В 13). Отметим флажком позицию Метки в первой строке (поскольку нам нужно сохранить заголовок этой графы), а затем в окне Выходной интервал укажем ячейку 1 1, в которой будет размещена таблица с рассчитанными показателями рангов и перцентилей. После этого — кнопка ОК. [c.33]
Заполните графу "Ранг" в таблице результатов, записав в нее результаты строки "Ранг" [c.414]
Ваш результат по графе Сильная сторона Ранг Обратный ранг Ограничение [c.414]
Впишите номера 1, 2, 3 из графы "Ранг" Впишите номера 1, 2, 3 из графы "Обратный ранг" [c.415]
Перенесите данные из графы "Обратный ранг" теста "Вы сами" таблицы результатов на странице 414 в графу Б предлагаемой ниже таблицы. [c.422]
Перенесите Ваши итоговые данные из бланка для ответов в соответствующую строку графы "Сумма" таблицы результатов. Заполните графу "Ранг", присваивая наибольшей сумме номер 1, а наименьшей —11. [c.427]
Ваш результат по графе Ограничение Сумма Ранг [c.427]
В приведенной группировке закон Энгеля, если идти по доходным группам, находит свое полное подтверждение. Подтверждается он вполне и более дробными подгруппами — по размеру семьи. Два-три отклонения в подгруппах с наименьшим числом бюджетов, разумеется, не опорочивают этой закономерности. С законом Швабе дело обстоит несколько хуже. Здесь с ростом благосостояния семейный расход на квартиру растет по общему правилу не только в абсолютных размерах, но и в проценте к общему расходу, что как будто переводит его из разряда наиболее настоятельных потребностей в ранг второстепенных нужд . Но для революционных лет, когда квартира стала почти бесплатной, это явление само по себе не вызвало бы больших сомнений. Кстати сказать, оно было уже отмечено, хотя и без должного объяснения, И. Н. Дубивской в ленинградских бюджетах за май 1918 г. Однако наше внимание привлекает здесь совсем другое явление. Сопоставляя графы 8 и 9 табл. 5 и 6, мы наблюдаем еще одну весьма ярко выраженную закономерность. Благосостояние группы растет в обратной зависимости к росту семьи и в прямой от размеров средней души в этой семье. Таким образом, процент расхода на пжщу можно сопоставлять не только с ростом обеспеченности семей, что делая Энгель, но и с сопутствующим ему фактом укрупнения души, чего Энгелъ не делал. [c.153]
Дуги графа целей символически можно представить в виде операторов R JV> где / — индекс, указывающий ранг цели, из которой выходит дуга / — номер вершины цели /-го ранга, из которой выходит дуга v — номер вершины (/ + 1) -го ранга, в которую входит дуга [c.59]
Алгоритм суммирования по рангам. По этой программе производится суммирование всех записей, имеющих п-е ранги, и сравнение их с записями, имеющими (п—1)-е ранги. Если вся информация, подлежащая контролю, помещается в оперативном накопителе или накопителе с произвольным доступом, то удобно проводить суммирование снизу вверх. Однако часто подлежат контролю большие массивы информации, которые в оперативный накопитель не помещаются. Они, как правило, записываются на магнитные ленты и могут вводиться в оперативный накопитель по частям в порядке возрастания шифров. Учитывая это, целесообразно проводить суммирование просмотром сверху вниз. Суть проверки состоит в следующем для каждой информационной записи массива отводится некая группа ячеек grupa [k, r]. Здесь k — номер элемента в строке, k меняется от 0 до числа, равного количеству граф в документе. При =0 (для всех г) ячейки grupa [0, г] предназначены для записи шифра строки или содержимого некоторого счетчика строк, по которому можно найти адрес строки, если она требует исправления. При k=, 2,... элементы этой группы содержат числовые показатели данной строки, г равен рангу строки г=0, 1, 2,..., 8. [c.73]
Затем аналогичным образом поступим с данными 3-й графы (сведения от фирмы Мельхиор ). При заполнении диалогового окна Ранг и персентиль отметим диапазон ячеек С 1 С 13, а для опции Выходной интервал покажем ячейку, которая должна быть по соседству с первой половинкой нашей общей таблицы. Это ячейка М 1. [c.33]
Заполните строку "Сумма" бланка для ответов, подсуммировав количество перечеркнутых клеток в каждой графе от А до К. Затем заполните строку "Ранг", присваивая наибольшему результату предыдущей строки "сумма" ранг 1, второму по величине графы А — ранг 2 и т. д. Наименьший результат получит ранг 11. [c.414]
Разобравшись с каждым из 110 утверждений, подсуммируйте количество перечеркнутых клеток в каждой графе от А до К и результаты впишите в графу "Сумма". Определите ранги каждой из 11 граф, а затем переходите к таблице результатов. [c.427]
Теорема 11.7. Ранг r(G) графа G равен числу ребер леса, а цикломатическое число ц(0) равно числу ребер КО-леса. , [c.263]
Ранг и цикломатическое число являются числовыми характеристиками графа, определяющими размериость подпространств циклов и разрезов. [c.263]
