Опорный план является допустимым решением ТЗ и используется в качестве начального базисного решения при нахождении оптимального решения методом потенциалов. Существует три метода нахождения опорных планов метод северо-западного угла, метод минимального элемента и метод Фогеля. "Качество" опорных планов, полученных этими методами, различается в общем случае метод Фогеля дает наилучшее решение (зачастую оптимальное), а метод северо-западного угла — наихудшее. [c.70]
Все существующие методы нахождения опорных планов отличаются только способом выбора клетки для заполнения. Само заполнение происходит одинаково независимо от используемого метода. Следует помнить, что перед нахождением опорного плана транспортная задача должна быть сбалансирована. [c.70]
Решение задачи начинается с нахождения опорного плана перевозок, который может быть определен с помощью так называемого метода северо-западного угла, метода минимального элемента и т. д. . . [c.71]
Пример 7.13. Решение задачи линейного программирования симплекс-методом. Для нахождения опорного плана использовать метод искусственных переменных. [c.222]
| Таблица 8.12 Пример нахождения опорного плана методом Фогеля | 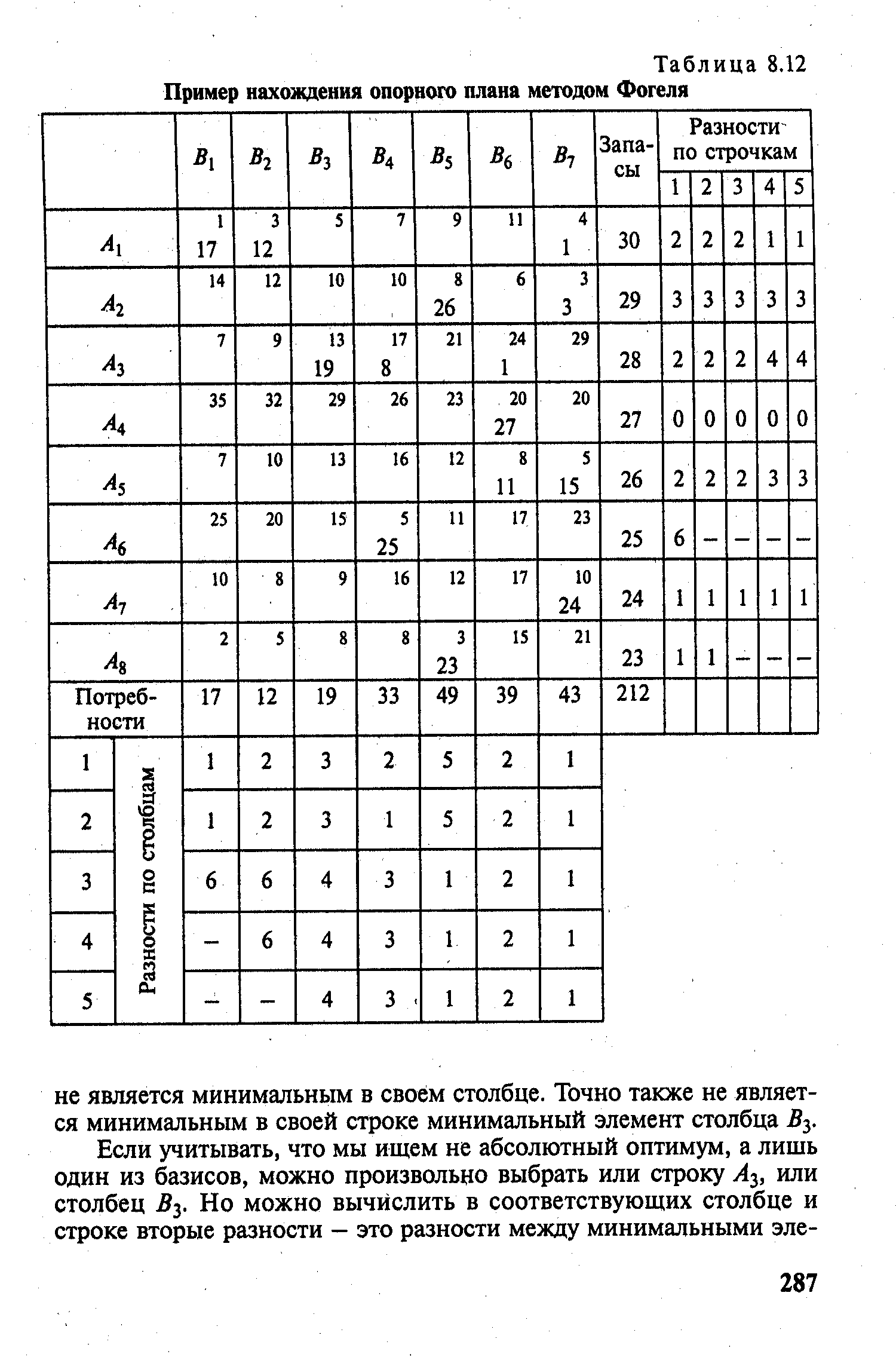 |
На первом шаге нахождения опорного плана методом Фогеля возникает ситуация равенства значений максимальных штрафов транспортной матрицы (см. табл. 5.3) [c.75]
Заметим, что предложенный в данной задаче многомерный аналог метода минимального элемента нахождения опорного плана транспортной задачи линейного программирования не требует исчерпания излишков у всех поставщиков необходимо лишь покрытие дефицитов (при этом по ключевой номенклатуре одновременно закрываются и излишки). [c.225]
Представим себе любую линейную оптимизационную задачу и кратко напомним основные особенности симплекс-метода. Его идея состоит в переходе от одного базисного (опорного) плана к другому таким образом, что линейная форма улучшается на каждом шаге и достигает экстремума. Переход происходит по вершинам выпуклого многогранника условий в я-мерном пространстве, причем на каждом шаге переход осуществляется в соседнюю вершину. При нахождении в такой вершине проводится проверка плана на оптимальность. Линейная форма (гиперплоскость) делит все пространство на две части. Вершинам, находящимся в верхней части, соответствуют отрицательные элементы целевой строки, а вершицам из нижней части — положительные. Переход осуществляется только в соседние вершины из верхнего полупространства до тех пор, пока в нем не останется ни одной вершины. Переход проводится в ту вершину, которой соответствует максимальный по абсолютной величине из отрицательных элементов целевой строки. Если на последнем шаге линейная форма имеет более одной общей точки с выпуклым многогранником условий, то имеется множество оптимальных пла- [c.60]
