| Рис. 2. Диаграмма коробка Эджуорта . | 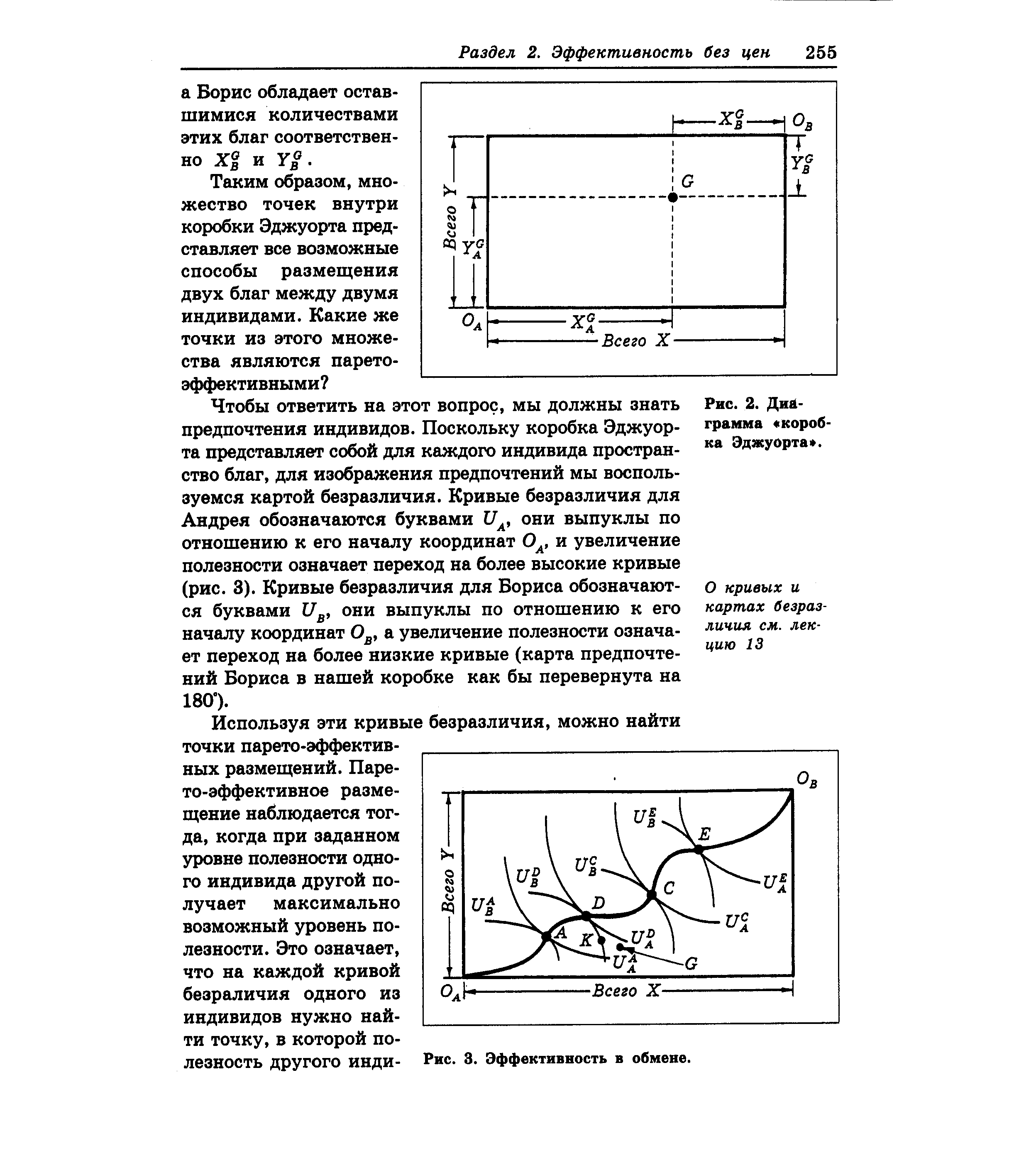 |
Чтобы ответить на этот вопрос, мы должны знать предпочтения индивидов. Поскольку коробка Эджуорта представляет собой для каждого индивида пространство благ, для изображения предпочтений мы воспользуемся картой безразличия. Кривые безразличия для Андрея обозначаются буквами UA, они выпуклы по отношению к его началу координат ОА, и увеличение полезности означает переход на более высокие кривые (рис. 3). Кривые безразличия для Бориса обозначаются буквами UB, они выпуклы по отношению к его началу координат ОВ, а увеличение полезности означает переход на более низкие кривые (карта предпочтений Бориса в нашей коробке как бы перевернута на 180°). [c.255]
Кривые предложения позволяют определить рыночное равновесие в коробке Эджуорта. Предположим, что в уже знакомой нам модели экономики обмена построены кривые предложения для Андрея и Бориса (ОСА и ОСВ на рис. 10). Они начинаются из одной точки а, представляющей некоторое исходное размещение благ X и Y, и лежат внутри области, ограниченной кривыми безразличия U и /f. Эти кривые предложения показывают реакции потребителей на изменения соотношения цен благ. [c.268]
Продемонстрировать это можно с помощью рис. 12, на котором изображены коробка Эджуорта и модель экономики обмена с двумя индивидами при наличии цен. В точке е, т. е. в точке касания кривой безразличия Андрея (UA) и кривой безразличия Бориса (UB), [c.274]
Благодаря Парето в экономическую теорию прочно вошли такие инструменты анализа, как кривые безразличия, карта безразличия , коробка Эджуорта и т.д. [c.242]
Таким образом, множество точек внутри коробки Эджуорта представляет все возможные способы размещения двух благ между двумя индивидами. Какие же точки из этого множества являются парето-эффективными Чтобы ответить на этот вопрос, мы должны знать предпочтения индивидов. Поскольку коробка Эджуорта представляет собой для каждого индивида пространство благ, для изображения предпочтений мы воспользуемся картой безразличия. Кривые безразличия для Андрея обозначаются буквами UA, они выпуклы по отношению к его началу координат ОА, и увеличение полезности означает переход на более высокие кривые (рис. 3). Кривые безразличия для Бориса обозначаются буквами Uв, они выпуклы по отношению к его началу координат Ов, а увеличение полезности означает переход на более низкие кривые (карта предпочтений Бориса в нашей коробке как бы перевернута на 180°). [c.98]
Продемонстрировать это можно с помощью рис. 12, на котором изображены коробка Эджуорта и модель экономики обмена с двумя индивидами при наличии цен. В точке е, т. е. в точке касания кривой безразличия Андрея (UA) и кривой безразличия Бориса (UB), имеет место парето-эффективное размещение благ X и [c.117]
На рис. 9.3 изображена коробка Эджуорта-Боули для двух потребителей в пространстве двух благ. Коробка Эджуорта-Боули представляет собой две карты безразличия, наложенные друг на друга таким образом, что одна из них повернута на 180°. [c.188]
| Рис. 9.3. Коробка Эджуорта-Боули для двух потребителей, Федора и Трифона | 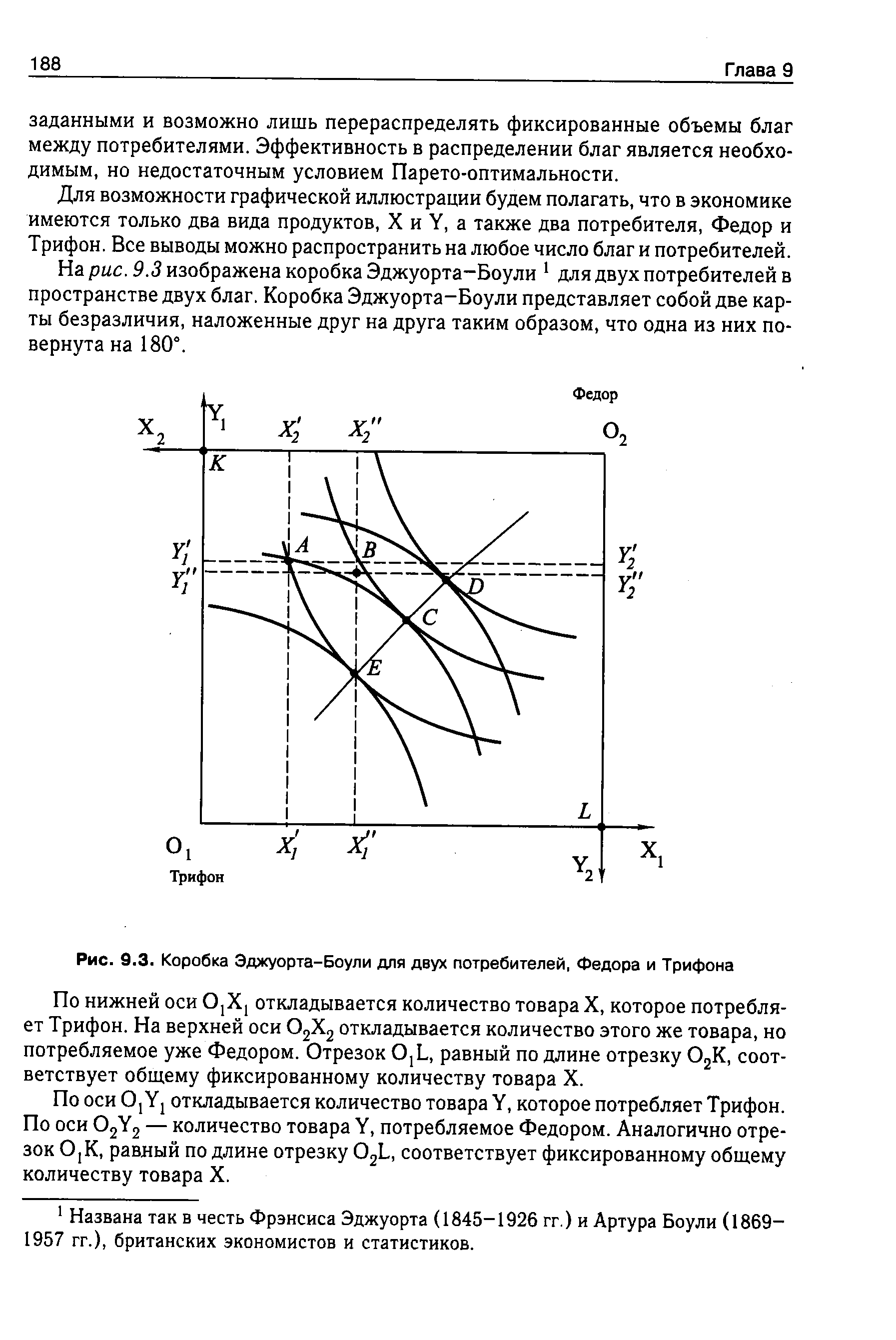 |
| Рис. 9.4. Коробка Эджуорта-Боули для двух предприятий | 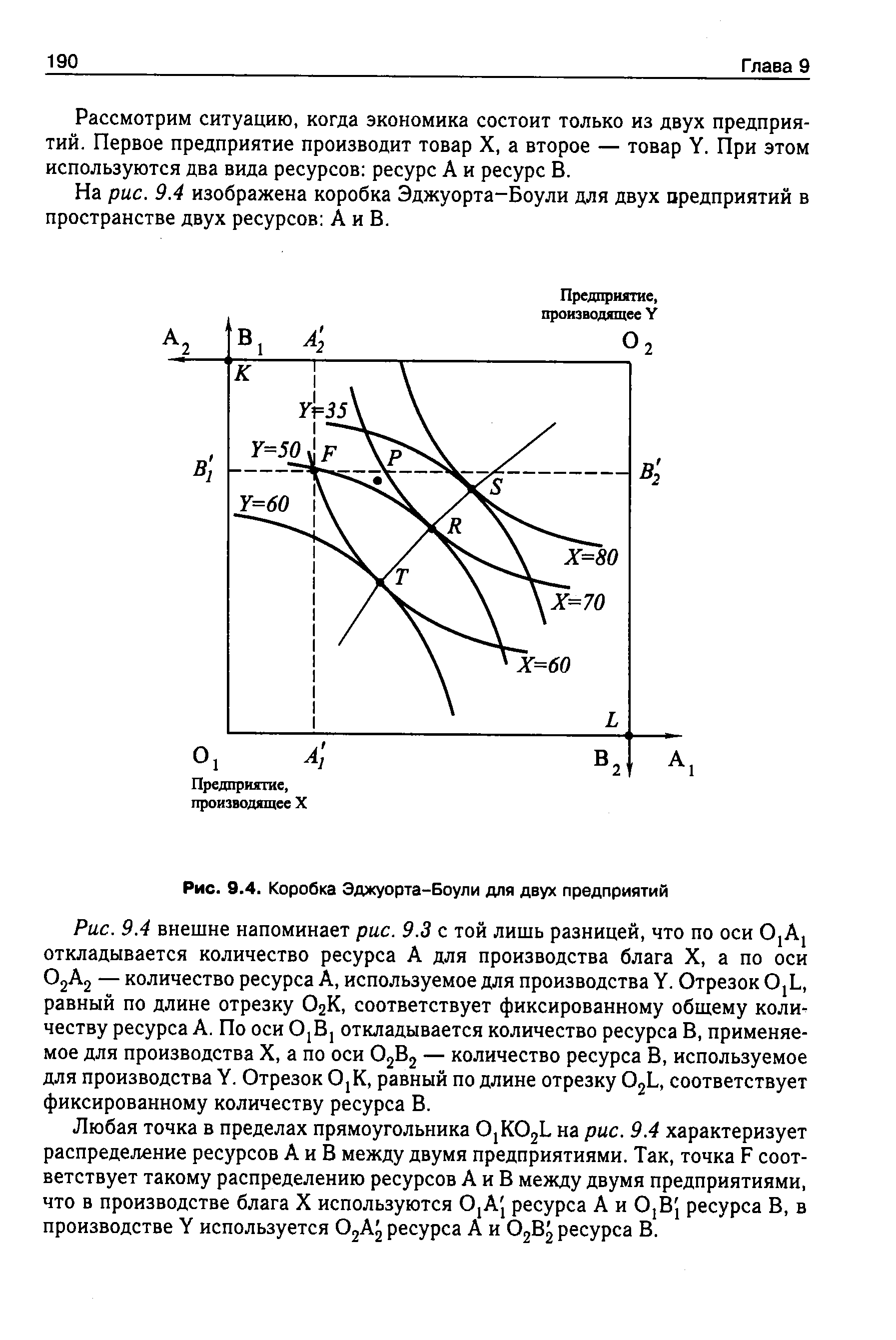 |
Отсюда получаем У, - Х,У,/Х2 => У, - Х,(210 - У1)/(210 - X,) => 210 У, --Х,У,"" 210 X, - X1Y1 = X, У, — уравнение контрактной кривой (на рис. 16 — диагональ квадрата, представляющего коробку Эджуорта). [c.721]
Коробка Эджуорта (Edgeworth box) — диаграмма, показывающая возможности взаимовыгодного обмена между двумя индивидами. Представляет собой прямоугольник, в котором совмещены карты безразличия обоих индивидов таким образом, что начала координат этих карт находятся в противоположных вершинах прямоугольника на осях координат отложены количества имеющихся у индивидов благ. На аналогичной диаграмме для производства совмещены карты изоквант, а на осях координат отложены количества факторов производства. В этом случае к. Э. показывает возможности эффективного замещения ресурсов [c.735]
