Аналогичным образом от описания в виде множества производственных возможностей (2.5) можно перейти к функции затрат. Для этого надо предположить, что производство данного неотрицательного объема продукции у достигается при минимальных затратах ресурса х. Из (2.5) получаем функцию [c.69]
Конечно, такая простая связь между множеством производственных возможностей и производственными функциями устанавливается лишь в случае одного продукта и одного ресурса. В общем случае переход от множества производственных возможностей (2.4) к производственной функции (2.1) требует построения множества всех эффективных точек множества (2.4), т. е. всех таких объемов затрачиваемых ресурсов и выпускаемой продукции, что при данных затратах нельзя выпустить большее коли- [c.69]
Рассмотрим множество производственных возможностей для производственного способа, заданного в виде -(4.14), (4.15). Оно имеет вид [c.101]
Если предположить, что избыток ресурсов не мешает производству, причем ресурсы могут использоваться неэффективно, то множество производственных возможностей представимо в следующем виде [c.101]
Для формы (4.16) множество производственных возможностей приобретает вид [c.101]
Как показывает пример (4.20)—(4.22), структурные модели можно использовать для построения теоретической производственной функции, опирающейся на предположение о рациональной организации производства. Построение теоретической производственной функции позволяет создать представление об идеально функционирующей производственной системе, оценить ее потенциальные возможности и на этой основе выявить потери, возникающие из-за недостатков экономического механизма. Как мы видели при анализе примера (4.20)—(4.22), график теоретической, идеальной производственной функции совпадает с множеством эффективных точек множества производственных возможностей. Поэтому для построения теоретических производственных функций необходимо иметь методы построения множества эффективных точек. Такие методы обсуждаются в гл. 6. [c.108]
Обратимся к стандартной модели, сформулированной в начале главы. Множество производственных возможностей имеет вид [c.339]
Формулировка проблемы. Рассмотрим проблему анализа систем стимулирования производства в том случав, когда Центр не имеет полной информации о возможностях производственных единиц. Рассмотрим проблему планирования производства (1.1), (1.3), (1.4), предполагая, что Центр знает вид множества производственных возможностей [c.358]
Пусть по-прежнему множество производственных возможностей г-го предприятия описывается соотношением [c.376]
Множество производственных возможностей. Экономист узнал, что он может посадить ананасы в первом месяце и получить во втором урожай, составляющий 1 /2 ананаса на каждый посаженный ананас. Как и раньше, если он съест все ананасы в первом месяце, у него не будет ничего для потребления во втором. Если же он не съест ни одного ананаса в первом месяце, он может посадить все 100 и получить 150 для потребления во втором месяце. Эти две возможности, а также все, расположенные на соединяющей их прямой, образуют множество производственных возможностей экономиста. Поскольку экономист — единственный потребитель на острове, это также и его новое множество потребительских возможностей. [c.77]
За исключением одной общей точки, новое множество производственных/потребительских возможностей экономиста лежит выше и правее исходного множества потребительских возможностей. Наклон прямой множества производственных возможностей равен —100/150 = — 2/3- Поэтому экономист должен отказаться от 2/3 ананаса в первом месяце, чтобы получить один ананас для потребления во втором месяце. Величина, обратная наклону прямой, равна 1 (2/3) = 3/2= 11/2J она показывает, что экономист получает 1 /2 ананаса во втором месяце за каждый ананас, посаженный в первом месяце, что дает величину предельного продукта капитала. [c.77]
МНОЖЕСТВО ПРОИЗВОДСТВЕННЫХ ВОЗМОЖНОСТЕЙ, ПРОИЗВОД- [c.202]
Множество производственных возможностей 202 [c.474]
Общеэкономическое множество производственных возможностей 293 [c.478]
Итак, мы рассмотрели связи, существующие между производственными функциями и основной планово-производственной задачей Канторовича, являющейся обобщением линейных оптимизационных задач. Неслучайно наиболее общие из встречающихся в литературе многочисленных определений производственной функции не противоречат по своей сути содержанию оптимизационных задач, а определение множества производственных возможностей как множества всех возможных сочетаний затрат и выпусков корреспондирует с определением области допустимых планов. При этом мы оставались в рамках наиболее простого с математической стороны случая линейности всех исследуемых зависимостей, т. е. в рамках предпосылки о пропорциональности затрат выпускам, и наоборот. [c.60]
Как известно, условия первого порядка показывают точки экстремума, а для нахождения собственно точки максимума требуется найти условия второго порядка. Для того чтобы условия второго порядка действительно показали точку максимума, соответствующую (3), требуется предположить вогнутость функции полезности (1) и выпуклость множества производственных возможностей. [c.407]
В результате в производстве нерыночной продукции, будь то регулирование, управление трансфертными платежами или непосредственное производство общественных благ, присутствует сильная и непреодолимая тенденция к избыточным издержкам, или, иначе говоря, к .-неэффективности.ь Нерыночное производство осуществляется внутри множества производственных возможностей. Если существуют технологические возможности снижения издержек, повышения производительности или реализации экономии от масштаба, то эти возможности будут проигнорированы или, в лучшем случае, использованы не в полной мере. Перемены приносят лишние хлопоты, издержки бездействия отсутствуют или крайне малы, а возможный выигрыш от осуществления перемен весьма неопределенный.6 [c.529]
XV. Выпуклость множества производственных возможностей [c.664]
Множество производственных возможностей и его граница [c.664]
Множество производственных возможностей фирмы или общества можно рассматривать с различных точек зрения. В лекции 22 рассматривалась фирма, причем для простоты предполагалось, что фирма производит единственный продукт. В этой связи использовалось множество производственных возможностей в (п+1)-мерном пространстве, п координат которого характеризовали затраты различных ресурсов, а одна координата — объем выпуска продукта. В этом выпуске в связи с иным характером обсуждаемых задач мы рассматриваем множество производственных возможностей (МПВ), или производственное множество общества в пространстве продуктов, которое мы будем обозначать символом >. [c.664]
| Рис. 3. Связь выпуклости множества производственных возможностей с вогнутостью функции трансформации. | 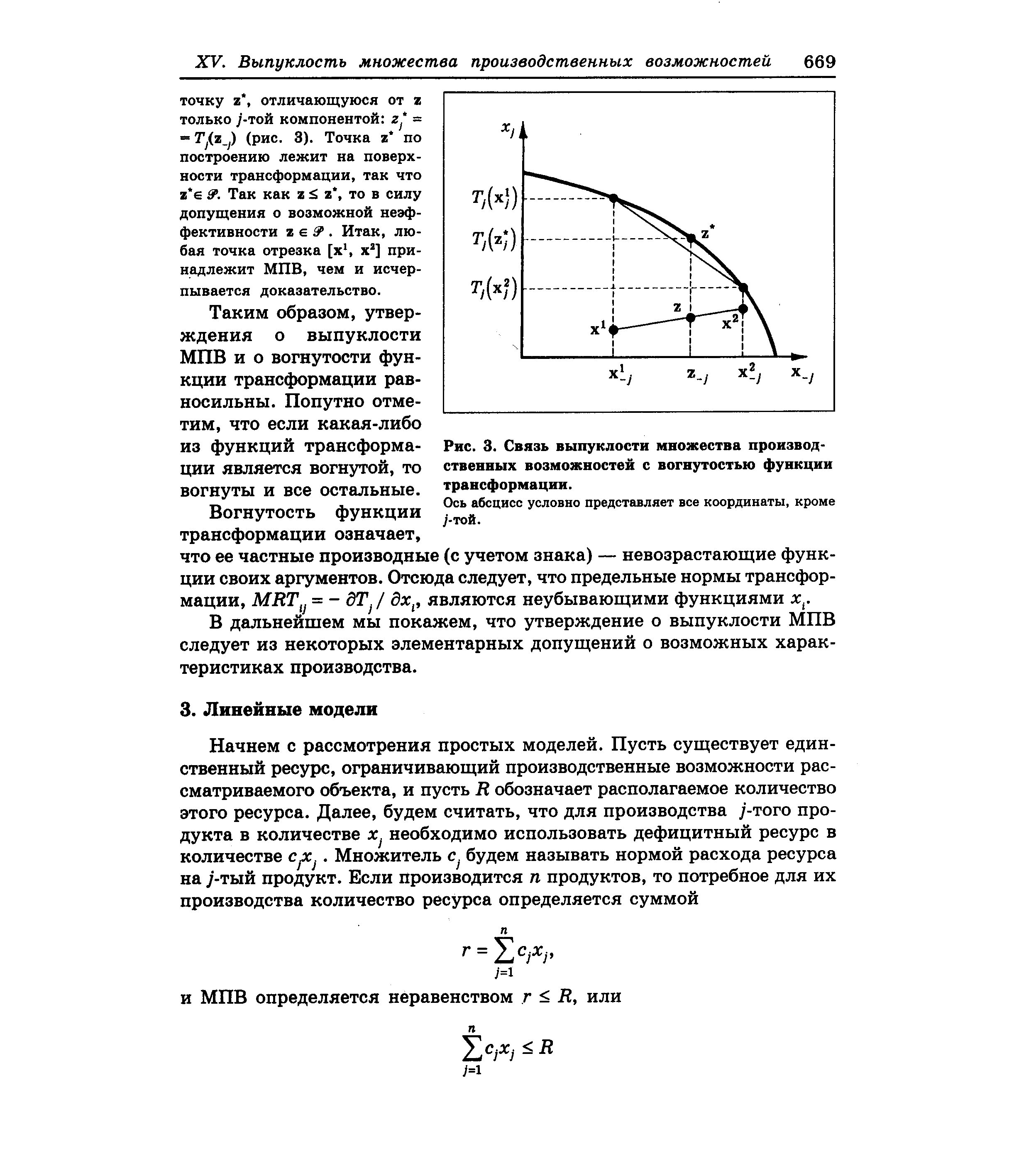 |
Предположим, что количество основных фондов для каждого производственного способа задано заранее, а количество трудовых ресурсов может изменяться. Тогда для /-го способа иптен-с. ниость К> не может превзойти величины ma = k /ko множество производственных возможностей приобретает вид [c.102]
Заинтересованность в увеличении прибыли может быть основана, например, на том, что материальное поощрение растет с ростом прибыли (1.8). Для того чтобы оценить плановые задания и объемы ресурсов, в которых заинтересована производственная единица, р ассмотрим вопрос о том, какой объем ресурсов и выпуск продукции приводит к максимизации прибыли (1.8) в том случае, когда множество производственных возможностей описывается соотношением (1.1). Прежде всего отметим, что при любом фиксированном Центром объеме ресурсов Xi максимум прибыли при любых положительных ценах р и q достигается при yi= Atl/Xi, [c.340]
Множество производственных возможностей показывает, сколько товаров или услуг может быть произведено в разные периоды времени. В модели робинзонады множество произ-водстненных возможностей и множество потребительских возможностей совпадают друг с дру (>м. [c.88]
Множество производственных возможностей (produ tion possibilities set) — все возможные варианты производства, которые имеются у индивида или фирмы на протяжении данного временного интервала. [c.90]
Построим на основе рис. 9.4 границу производственных возможностей. На рис. 9.5 по горизонтальной оси ОХ отложим объем производства товара X, по вертикальной оси OY — товара Y. Каждая из точек на контрактной линии (рис. 9.4) является точкой касания двух изоквант. Так, точке R соответствует точка касания изоквант при X = 70, a Y = 50. Соответствующую точку отметим на рис. 9.5. Точка S является точкой касания изоквант при X = 80, a Y = 35. Соответственно и ее нанесем на рис. 9.5 и т. д. Таким образом можно получить всю границу производственных возможностей ITRSK. Фигура, ограниченная этой кривой, есть множество производственных возможностей. Любая комбинация объемов X и Y, принадлежащая этому множеству, достижима. При этом состояние экономики не является эффективным в производстве. [c.191]
Теперь сделаем еще один шаг наложим на множество производственных возможностей коробку Эджуорта-Боули для двух потребителей таким образом, чтобы совместить начало координат для Трифона с точкой О, а начало координат для Федора — с точкой R. Кривая OR представляет собой контрактную линию. Рассмотрим распределение двух благ между потребителями, соответствующее точке С. Это распределение принадлежит контрактной линии. Находясь в этой точке, Трифон из общего количества в 70 единиц блага X получает 30 единиц блага X, а Федор — 40. Из общего количества блага Y в 50 единиц Трифон получает 30 единиц, а Федор — 20. Как было уже сказано, все точки, принадлежащие контрактной линии, являются точками касания двух кривых безразличия этих потребителей и при этом предельные нормы замены у них равны. Предположим, что в точке С предельные нормы замены для двух кривых безразличия равны 0,6 MRSX = MRSxrY= 0,6. Из рисунка видно, что касательная к кривой безразличия, проведенная через точку С, имеет меньший наклон, чем касательная к границе производственных возможностей, которая проведена через точку R. [c.192]
ВЕКТОР "ЗАТРАТ — ВЫПУСКА" [input-output ve tor] — вектор, содержащий компоненты двух видов выпускаемые продукты (обычно эти компоненты положительные) и продукты, затрачиваемые в производстве (отрицательные). Последние называют также факторами. В. "з.-в." называется допустимым, если продукты в количествах, определяемых его положительными компонентами, могут быть действительно произведены при затрате продуктов, определяемых отрицательными компонентами. Иными словами, если зафиксированный в данном векторе вариант плана производственной единицы реален (обеспечен достаточными/ су/ гши), то он допустимый. Совокупность допустимых В."з.-в." образует множество производственных возможностей (производственное пространство). [c.43]
ГРАНИЦА (множества) [boundary] — множество всех граничных точек данного множества. Напр., Г. допустимого множества в задаче математического программирования, Г. множества производственных возможностей (производственная граница). [c.67]
Будем считать все продукты неограниченно делимыми и примем допущение о возможной неэффективности1 если вектор х принадлежит МПВ, то в этом множестве найдется также любой вектор z, такой, что х > z, т. е. если можно из имеющихся ресурсов произвести набор продуктов х, то можно также произвести любой набор z, в котором каждого продукта не больше, чем в наборе х. Иными словами, мы исключаем ситуацию, представленную на рис. 2,а здесь не все точки, лежащие левее и ниже точки х, принадлежат МПВ. На рис. 2,6 через эффективную точку х множества производственных возможностей [c.665]
| Рис. 7. Множество производственных возможное- и в предыдущем пунк- | 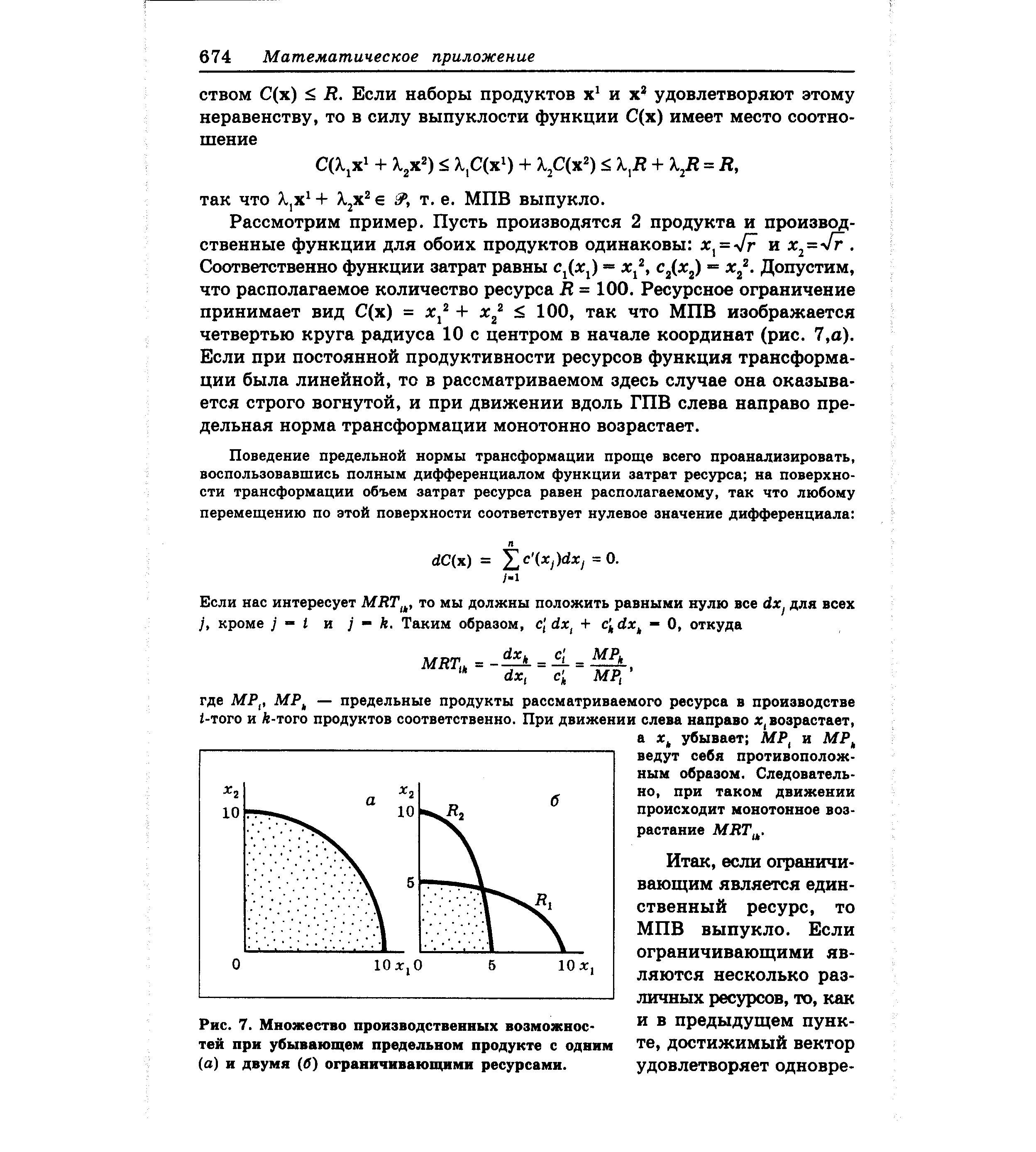 |
Смотреть страницы где упоминается термин Множество производственных возможностей
: [c.69] [c.69] [c.69] [c.70] [c.104] [c.76] [c.77] [c.851] [c.33]50 лекций по микроэкономике Том 2 (2000) -- [ c.2 , c.407 , c.431 , c.433 , c.458 , c.459 , c.529 , c.664 , c.665 , c.666 , c.667 , c.668 , c.669 , c.670 , c.671 , c.672 , c.673 , c.674 , c.675 , c.676 , c.677 , c.678 , c.679 ]
