Экономический смысл данной линии состоит в том, что она отражает все возможные комбинации С и С2, удовлетворяющие многопериодному бюджетному ограничению. Линия MN показывает две возможные альтернативы поведения домохозяйства. Во-первых, оно может превратить свой будущий доход в сегодняшний, взяв кредит под г %. Этой ситуа- [c.449]
| Рис. 22.5. Многопериодное бюджетное ограничение и различные комбинации потребления | 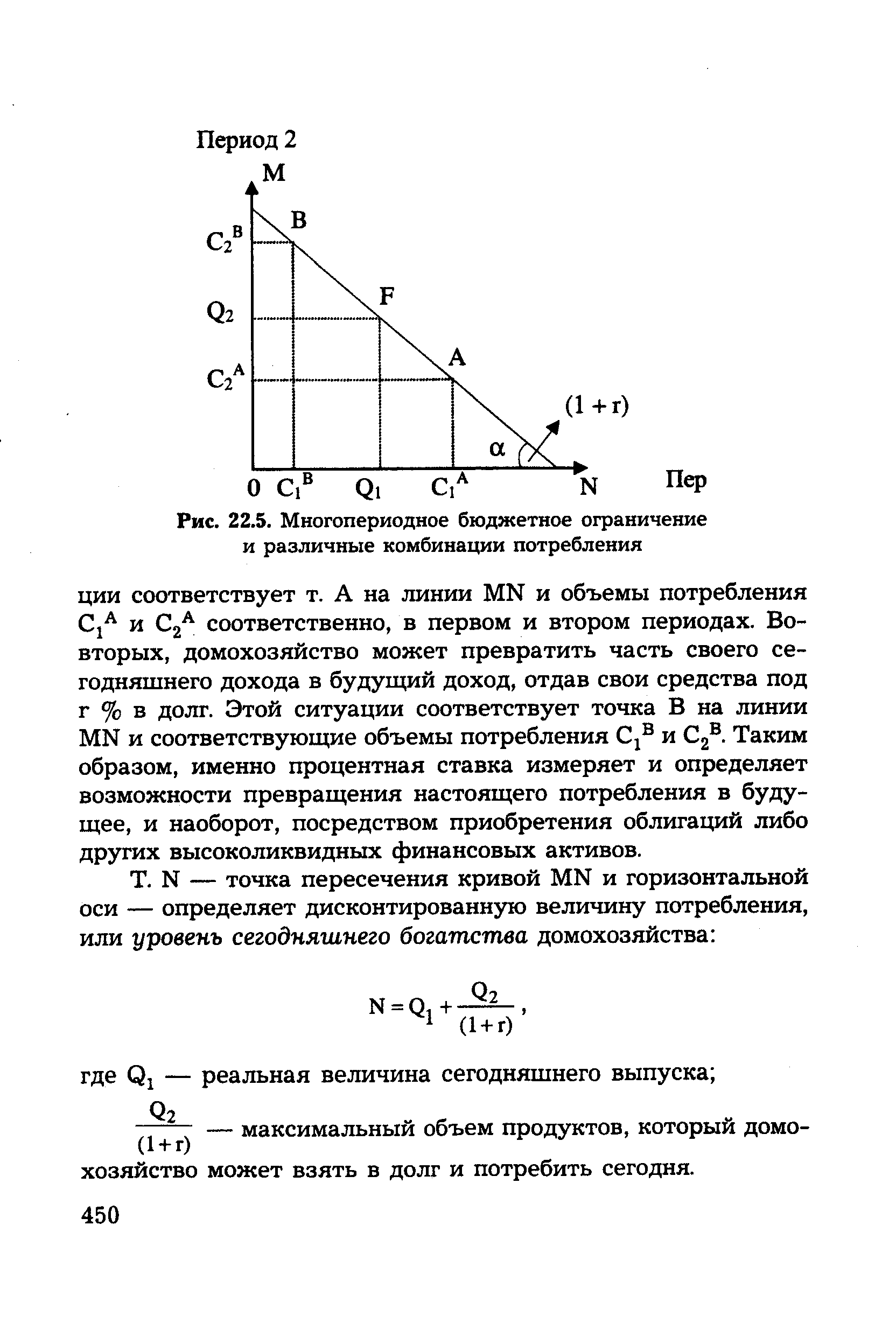 |
Перманентный доход (Y ) есть средняя величина настоящих и будущих доходов. В частности, для домохозяйства с неустойчивым уровнем дохода перманентный доход определяется как постоянный уровень дохода, обеспечивающий ему то же многопериодное бюджетное ограничение, что и при изменяющемся объеме дохода. То есть равенство [c.453]
Многопериодное бюджетное ограничение. [c.94]
Максимизируя (7) при многопериодном бюджетном ограничении [c.99]
Динамическое (многопериодное) бюджетное ограничение [c.111]
Бюджетное ограничение в соотношении (4.6) можно легко изобразить на графике, если мы запишем его в виде С2 = Q2 - (1 + г)С + (1 + + / ) >,. Очевидно, что бюджетное ограничение — это прямая с углом наклона — (1 + / ), которая проходит через точку (( ,, ( 2). Эта прямая представляет все возможные комбинации потребления (Ср С2), удовлетворяющие многопериодному бюджетному ограничению. Домашнее хозяйство может выбрать любой вектор потребления на этой прямой. Оно может превратить свой будущий доход в сегодняшний, взяв кредит под г процентов, или передвинуть часть своего сегодняшнего дохода в будущее, отдав свои средства в долг под г процентов. Следовательно, г измеряет возможности превращения настоящего потребления в будущее и наоборот посредством приобретения ценных бумаг. [c.114]
Из этих соотношений нетрудно получить многопериодное бюджетное ограничение для выплаты дивидендов [c.137]
Двухпериодная модель, делящая срок жизни домохозяйства на две части — настоящее и будущее, значительно упрощает исследование выбора многопериодной траектории потребления. Эта модель позволяет нам с помощью несложного графика найти точку равновесного потребления наложением кривых безразличия на многопериодное бюджетное ограничение. [c.139]
Далее объединим соотношения (5.5) и (5.6), для чего перепишем (5.5) в виде Bl = Ql — С, — /,, а затем подставим выражение для В в (5.6). После этих операций многопериодное бюджетное ограничение для домашнего хозяйства можно записать в виде [c.152]
Сальдо счета текущих операций имеет многопериодный аспект, что очень важно. Экономика в целом, как и домашние хозяйства (и фирмы), составляющие эту экономику, имеет многопериодное бюджетное ограничение. Если сегодня в экономике наблюдается дефицит счета текущих операций, то растет чистая задолженность резидентов страны остальному миру. В конце концов, внутреннее потребление придется урезать, чтобы платить проценты по накопленным долгам. С сокращением внутреннего потребления все большая часть внутреннего продукта становится объектом чистого экспорта. Фактически с помощью чистого экспорта обеспечивается выплата процентов по обязательствам, накопленным в период, когда сальдо счета текущих операций было отрицательным. [c.180]
Многопериодные бюджетные ограничения страны [c.197]
Многопериодное бюджетное ограничение в двухпериодной модели [c.198]
Многопериодное бюджетное ограничение страны можно исследовать формально с помощью двухпериодной модели. Предположим, как ранее мы делали при рассмотрении домашнего хозяйства, что страна начинает движение с нулевыми зарубежными активами (ffQ = 0). В этом случае величина В в первом периоде (5, ) будет равна активному сальдо счета текущих операций в первом периоде [c.198]
Многопериодное бюджетное ограничение для страны алгебраически можно представить несколькими способами. Во-первых, мы видели, что дисконтированная величина потребления должна быть равна дисконтированной величине выпуска за вычетом инвестиций. Во-вторых, можно перегруппировать члены уравнения (6.17) таким образом, чтобы получить соотношение для торгового баланса за два периода. Поскольку ТВ1 = ( , — — С, — /,, а ТВ2 = Q2— 2, то несложно убедиться в равенстве нулю дисконтированной величины торговых балансов [c.199]
Третий путь — выражение многопериодного бюджетного ограничения в терминах счета текущих операций. Поскольку для экономики в целом сальдо счета текущих операций равно сумме накопленных зарубежных чистых активов, мы имеем СА = В — В 0, а СА2 = 5 — В, . Предположим, страна начинает с нулевых зарубежных активов (В = 0) и заканчивает также с нулевыми активами (В 2 = 0). Тогда [c.200]
Многопериодное бюджетное ограничение для множества периодов [c.201]
До сих пор мы рассматривали многопериодное бюджетное ограничение для случая двух периодов. Однако не составляет труда применить наш анализ к случаю с большим числом периодов. Для Т периодов, если Т > 2, мы получаем выражения, аналогичные соотношениям (6.17), (6.18) и (6.19), из которых следует, что дисконтированная стоимость потребления должна быть равна дисконтированной стоимости выпуска за вычетом инвестиций приведенная величина торговых балансов должна равняться нулю сумма сальдо счета текущих операций между t = О и t = Т также должна быть равна нулю. [c.201]
Страны, как и люди, связаны многопериодным бюджетным ограничением дисконтированная стоимость совокупного потребления должна быть равна дисконтированной стоимости внутреннего выпуска минус дисконтированная величина инвестиций плюс исходные чистые инвестиции за рубежом. Это положение можно сформулировать иначе. Если страна является чистым должником, то в будущем она должна иметь положительное сальдо торговых балансов с дисконтированной стоимостью, равной ее начальному чистому долгу. [c.211]
Предположим, рис. 6-11 отображает случай двух больших стран в первом периоде двухпериодной модели. Как должны выглядеть две схемы во втором периоде Какие кривые должны сместиться, чтобы благосостояние обеих стран достигло максимума с учетом их многопериодного бюджетного ограничения [c.213]
Фискальная политика правительства воздействует на поведение домашних хозяйств через влияние налогов на их многопериодное бюджетное ограничение. Двухпериодное бюджетное ограничение домашних хозяйств записывается в терминах дохода за вычетом налогов, и поэтому изменение в налогах прямо влияет на это ограничение. Чтобы показать, как это происходит, перепишем соотношение (4.15) в виде [c.230]
Теоретическая важность анализа сокращения налогов, при котором остается неизменной их приведенная стоимость, становится несомненной, когда мы вводим многопериодное бюджетное ограничение для правительства. Правительства, как и домашние хозяйства, должны балансировать свои расходы и доходы во времени, хотя и не обязательно в каждом периоде. Чтобы убедиться в этом, мы можем вывести двухпериодное бюджетное ограничение для правительства, используя соотношение (7.2). Точно так же, [c.235]
Комбинируя эти два соотношения, мы можем (как и в случае домашних хозяйств) получить многопериодное бюджетное ограничение для правительства [c.236]
Как это должно отражаться на эквивалентности Рикардо Теорема утверждает, что для данного временного распределения государственного потребления (С, и Сч), государственных инвестиций (f и Д) и долга в конце второго периода ( 2) временная структура потребления (С, и С2) не зависит от временной структуры налогов (Т и Т2). Это легко доказать, по крайней мере теоретически, используя соотношения (7.12) и (7.14). Из бюджетного ограничения для правительства (7.14) можно увидеть, что для заданных С,, G2, f , Аи Щ приведенная стоимость налогов также является заданной величиной. Из (7.12) видно, что бюджетное ограничение домашних хозяйств зависит не только от временной структуры налогов, но и от их приведенной стоимости. Поэтому изменения Т и Т2, оставляющие постоянной сумму (Т + Т2)/(1 + г), не влияют на многопериодное бюджетное ограничение домашнего хозяйства. [c.236]
Теоретическая модель, которую мы используем для анализа государственных расходов и налогов, остается очень простой. В частности, мы предположили, что государственные расходы оказывают влияние на частный сектор в основном через многопериодное бюджетное ограничение и воздействие налогов и расходов на ставку процента. Конечно, существуют и другие важные каналы, через которые фискальная политика и решения о частных расходах могут влиять друг на друга. [c.243]
Фискальная политика государства непосредственно воздействует на поведение частного сектора через многопериодное бюджетное ограничение домашних хозяйств. Временное увеличение налогов вызывает временное уменьшение располагаемого дохода, что, в свою очередь, ведет к падению частных сбережений. Постоянное увеличение налогов сокращает постоянный располагаемый доход. Это приводит к падению частного потребления приблизительно на ту же величину, и поэтому постоянное увеличение налогов оказывает лишь небольшое влияние на частные сбережения. [c.250]
Предположим, в двухпериодной модели предпочтения людей таковы, что они желают полного выравнивания потребления во времени (С, = С2). Временной горизонт правительства больше, чем у домашних хозяйств, так что правительство имеет определенную величину долга в конце второго периода, т. е. его многопериодное бюджетное ограничение имеет вид С, + + Q2/(l + г) = Т +Т2/(1 + г)+Щ/( + г). Структура этой экономики такова объем производства у домашних хозяйств составляет Q = 200, Q, = = ПО государственные расходы С, = 50, С2 = ПО налоги Т = 40, Т2 = = 55 процентная ставка г = 10. При этом [c.253]
Существование денег оказывает воздействие на многопериодное бюджетное ограничение домашнего хозяйства, так как деньги являются альтернативным активом, в форме которого домашние хозяйства могут хранить свои сбережения. Хранение денег по сравнению с хранением облигаций характеризуется альтернативными издержками, равными упущенному проценту. Эти альтернативные издержки представляют собой возрастающую функцию от номинальной процентной ставки и уровня реальных денежных остатков. [c.284]
Соотношение (4.6) представляет собой многопериодное бюджетное ограничение домашнего хозяйства. Его смысл состоит в том, что приведенная стоимость потребления должна быть равна приведенной стоимости выпуска. Приведенную стоимость выпуска можно также рассматривать как богатство домашнего хозяйства (W ) в начале первого периода (до того, как домашнее хозяйство определило объем потребления в первом периоде). Фундаментальное условие, которое описывается этим соотношением, может быть обосновано и на интуитивном уровне. Домашние хозяйства в какой-то конкретный период могут потреблять больше своего дохода. Но в течение всей жизни их объем потребления, очевидно, не может быть больше размера средств, которыми они располагают, при этом, как мы условились, домашние хозяйства и не потребляют меньше, чем имеют, и не оставляют наследства. Условие приведенной стоимости означает, что семья может выбрать любое распределение потребления по периодам (С, и С2), удовлетворяющее требованию приведенная стоимость потребления равна приведенной стоимости дохода. Домашнее хозяйство должно жить по средствам не от периода к периоду, а в течение всей жизни4. [c.112]
Согласно модели перманентного дохода потребление соответствует перманентному доходу (Yp), который определяется как некая средняя величина настоящих и будущих доходов. В частности, для домашнего хозяйства с неустойчивым уровнем дохода Yp определяется как постоянный уровень дохода, который обеспечивает домашнему хозяйству то же многопе-риодное бюджетное ограничение, что и при изменяющемся объеме дохода. Формально это выглядит следующим образом. Многопериодное бюджетное ограничение домашнего хозяйства (для двух периодов) имеет вид С, + С2/(1 + / ) = С , + ( 7/(1 + г), где ( , и Q2 обычно не равны. А теперь найдем такое значение Yp, при котором домашнее хозяйство будет иметь то же самое многопериодное бюджетное ограничение, которое было бы при выпуске Yp в каждом из периодов. Очевидно, что Yp должно удовте-творять равенству (4.9) [c.118]
Начало современному7 анализу потребления и сбережений положил Джон Мейнард Кейнс. Он впервые ввел понятие функции потребления, связывающей текущее потребление с текущим доходом. Этот подход, явившийся важным шагом в развитии экономического анализа, был впоследствии вытеснен исследованием потребления и сбережений с учетом фактора многопе-риодности, основанным на идее о том, что домашнее хозяйство распределяет свой доход между потреблением и сбережениями с целью максимизации полезности. При этом выбор объемов текущего потребления и сбережений зависит не только от текущего дохода, как в кейнсианской модели, но и от ожидаемого будущего дохода и ставки процента. При выборе траектории потребления домашние хозяйства связаны многопериодным бюджетным ограничением, которое заключается в том, что приведенная стоимость потребления должна быть равна приведенной стоимости выпуска домашнего хозяйства в сумме с ценными бумагами, которые оно получило в наследство, за вычетом приведенной стоимости наследства, которое домашнее хозяйство оставляет своим детям. [c.139]
Многопериодное бюджетное ограничение для страны иногда определяют через чистый трансферт ресурсов (NRT), который должна осуществить страна. NRT измеряет потоки наличности между страной и всеми ее кредиторами, т.е. чистые займы, предоставленные стране ее кредиторами, за вычетом процентов, которые страна выплачивает по своей внешней задолженности. Тогда NRTza период t определяется выражением [c.203]
Какие t и (2 необходимо выбрать Мы знаем, ч го правительство должно соблюдать многопериодное бюджетное ограничение, при котором дисконтированная стоимость налоговых поступлений должна быть равна дисконтированной стоимости государственных расходов, но мы также знаем, что бюджет не обязательно должен быть сбалансированным в каждом периоде. Если правительство пытается сбалансировать бюджет в каждом периоде и если С, намного больше, чем G2, то, по всей вероятности, t будет намного больше, чем /2 (если, конечно, У, не оказывается намного большим, чем Y2, и в этом случае база налогообложения также больше в первый период). Однако Барро доказывает, что такая политика не обязательно будет вести к высоким издержкам от искажающего влияния налогов. [c.246]
Государственные расходы воздействуют на частный сектор не только через многопериодное бюджетное ограничение и изменение в процентных ставках, но и по множеству других каналов. К примеру, большинство налогов взимаются с доходов, расходов или собственности и не являются поэтому фиксированными. Вледствие этого уровень налогов влияет на частные решения относительно предложения труда, сбережений и инвестиций. Как правило, подоходные налоги влияют на предложение труда. Хотя направление этого влияния теоретически является неопределенным (так как эффекты замещения и дохода действуют в противоположных направлениях), но эмпирически установлено, что рост подоходного налога ведет к. уменьшению предложения труда. Налогообложение личных доходов может влиять также на решения относительно сбережений, а налоги на доходы корпораций воздействуют на инвестиционные решения. [c.251]
Это бюджетное ограничение можно записать в виде, более похожем на бюджетное ограничение стандартной теории потребления. Пусть Рг — цена потребления во втором периоде в единицах потребления первого периода. Заметим, что для увеличения потребления во втором периоде на единицу необходимо снизить потребление в первом периоде на /( +/ ) единиц (иными словами, увеличить сбережения на эту сумму). Таким образом, Рг = ( +/ ). Очевидно, что цена товаров потребления в первом периоде в единицах потребления первого периода равна 1. Это позволяет сформировать систему цен (которые можно назвать динамическими многопериодными ценами), при которой цена товаров второго периода выражается в единицах товаров первого периода. Используя эти цены, мы можем записать бюджетное ограничение как / [С, + РгСг PlQl + /"jQj, что внешне выглядит как обычное бюджетное ограничение для потребителя. [c.112]
