Ключевой проблемой, возникающей при поиске ответа на данный вопрос, является проблема издержек, которые несут клиенты в случае перехода из одного банка в другой. Ее можно достаточно наглядно проиллюстрировать в рамках двухпериодной модели распределения клиентов по банкам. В данной модели рассматривается поведение банков и их потенциальных вкладчиков в течение двух этапов. На первом этапе перед банками стоит задача привлечения клиентов, а перед клиентами, соответственно, — выбора банка. На втором этапе клиенты решают остаться на обслуживании в ранее выбранном банке или перейти в другой. Очевидно, что если издержки, связанные с переходом в новый банк ( издержки переключения 2), высоки, то клиенты оказываются запертыми в ранее выбранном банке. Последнее меняет характер конкуренции на втором этапе и позволяет банкам назначать монопольные цены. [c.126]
Ожидаемая цена в момент времени t = 1 в нашей двухпериодной модели соответствует ожидаемому денежному потоку Е[Х] проекта. Сегодняшняя стоимость — это цена в момент времени t = 0. Приравнивание (4.81) к САРМ приводит к [c.215]
В рамках многопериодной биномиальной модели можно определить цену опциона и тогда, когда число возможных конечных значений цены акции больше двух. Если, например, в двухпериодной модели положить и = l/d, то два из четырех возможных конечных значений цены сольются, Sud = Sdu = S если дополнительно предположить, что Sdd < А < S < Suu, то возникает задача с тремя состояниями, которая не может иметь решения в рамках биномиальной модели. Тем не менее решение есть даже в более общем случае, когда и l/d. В чем же здесь дело [c.93]
Какой бы ни реализовался исход в момент времени /= 1 (т.е. окажется ли цена акции равной uS или dS), вероятность того, что в момент времени / = 2 цена акции будет в и раз больше, нежели она была в момент t=l, равна q, а вероятность того, что в момент времени t = 1 цена акции будет в d раз меньше, нежели она была в момент t=, равна (1 - q). На следующем графике рассмотрена двухпериодная модель (рис. 35). [c.254]
Рассмотрим двухпериодную модель и предположим для простоты, что потребитель не обладает никакими первоначальными активами (то есть Во=0) и не планирует оставлять наследство в конце жизни (В2=0). Тогда сбережения первого периода составят [c.94]
Рис 1. Графическое представление двухпериодной модели потребления [c.96]
Согласно теории жизненного цикла жизнь можно разделить на несколько периодов, которые характеризуются разными уровнями доходов. Для того, чтобы можно было использовать двухпериодную модель потребления, рассмотренную выше, условно разделим жизнь на два периода первый период будет соответствовать тому времени, когда человек работает и получает высокий доход, а второй период- время, когда человек на пенсии и имеет низкий доход. [c.97]
В терминах двухпериодной модели потребления, если потребитель начинает свою жизнь без каких-либо первоначальных активов, то богатство, подсчитанное в период 1 (Wi), представляет собой [c.98]
Учитывая стремление потребителя сглаживать траекторию потребления (то есть поддерживать одинаковый уровень потребления при изменяющемся доходе) мы находим, что в двухпериодной модели имеет место следующая зависимость между потреблением и богатством [c.98]
В частности, для двухпериодной модели мы получаем, что перманентный доход равен [c.99]
Парадокс Кузнеца в свете современных теорий потребления Посмотрим, как современные теории потребления позволяют объяснить различие в краткосрочной и долгосрочной динамике потребления. С точки зрения теории перманентного дохода, потребление определяется не текущим, а усредненным жизненным доходом, который называют перманентным доходом. Более строго, в рамках двухпериодной модели потребление может быть выражено следующей формулой [c.100]
Предположим, что для оживления экономики государство планирует снизить налоги в первом периоде в рамках двухпериодной модели. Если снижение налогов не сопровождается снижением государственных расходов, то есть, госзакупки и государственные трансферты остаются на прежнем уровне, то в результате образуется бюджетный дефицит. Будем считать, что дефицит покрывается за счет заимствования у населения (продажи населению государственных облигаций). В результате увеличивается государственный долг. Мы можем проиллюстрировать происходящие изменения, обратившись к бюджетному ограничению государства. Считая, что первоначальный долг государства равен нулю ( >о=0), мы получаем для первого периода (14) Сг+Щ-ТАг=Ог. [c.101]
Посмотрим, как подобная политика отразится на потреблении. Проанализируем бюджетное ограничение потребителя в двухпериодной модели. Перепишем ограничение (5), принимая во внимание наличие паушальных налогов (государственные трансферты для простоты будем считать нулевыми) [c.102]
Рассмотрим двухпериодную модель для домохозяйства, как мы это делали при выборе решения о потреблении, однако введем дополнительные возможности для перераспределения ресурсов между периодами. Предположим, что часть ресурсов (Ij) в первом периоде можно направить на инвестиции, которые позволят увеличить выпуск во втором периоде на величину F(K), где -производственная функция иК=1]. Считая, что капитал полностью изнашивается за один период, получаем следующее бюджетное ограничение [c.109]
| Рис. 1. Разделение решений о производстве и потреблении в двухпериодной модели. | 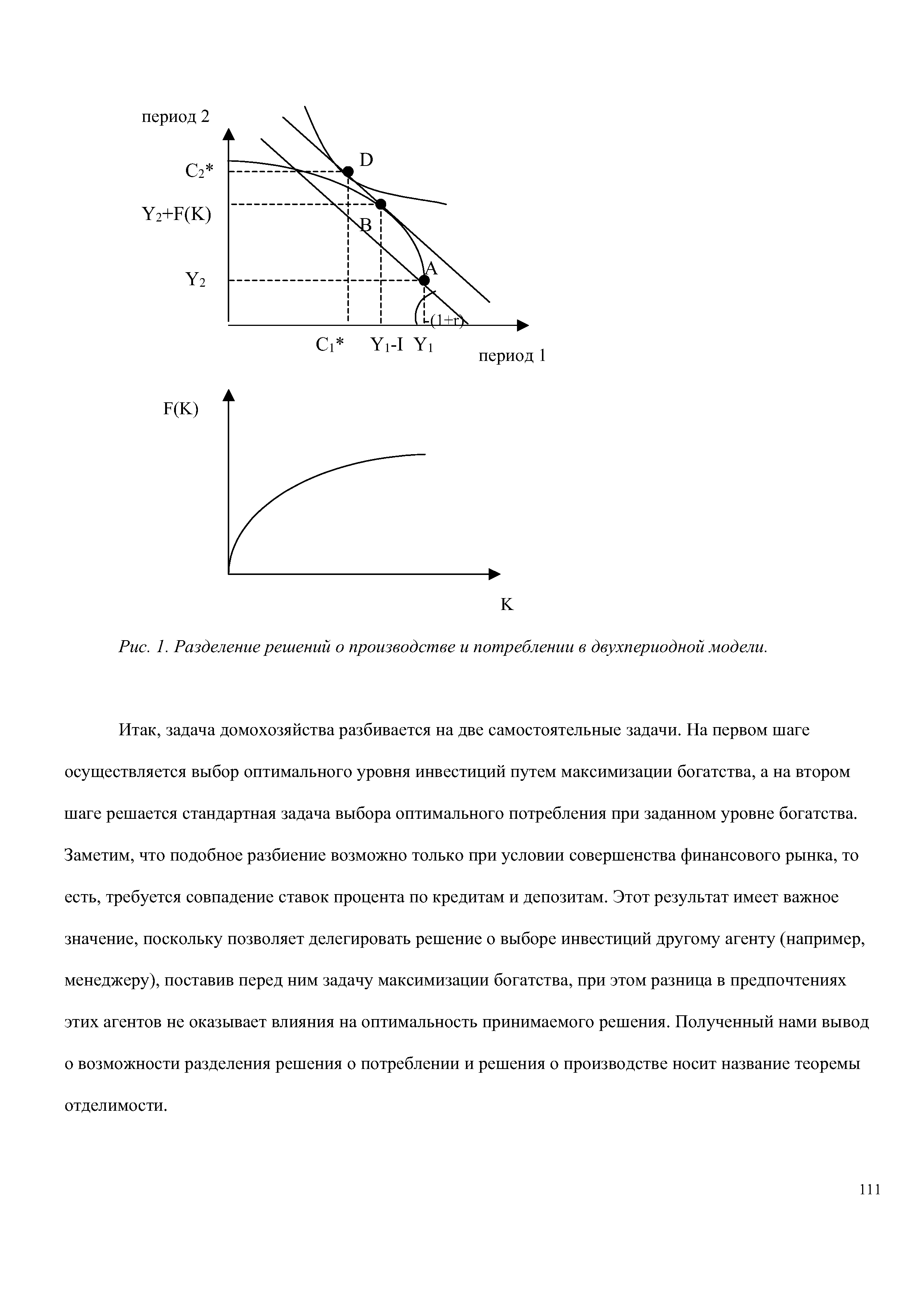 |
Мы проиллюстрируем этот анализ на основе следующей простой двухпериодной модели. [c.255]
Рассмотрим в общем виде двухпериодную модель потребительского поведения U( 1, 2) max (1) [c.195]
В двухпериодной модели потребительского выбора функция полезности потребителя [c.200]
Обозначим t - годовую ставку инфляции. Тогда бюджетное ограничение (2) в двухпериодной модели (1) - (3) можно записать так [c.201]
Бюджетное ограничение в двухпериодной модели [c.111]
Двухпериодная модель обладает тем преимуществом, что ее легко можно представить графически. Отложим на горизонтальной оси рис. 4-2 переменные первого периода, а на вертикальной оси — переменные второго периода. Точка Q представляет распределение, которое отражает конкретную комбинацию выпусков домашнего хозяйства в первом и во втором периодах. Другими словами, точка Q задана вектором (( ,, Q2). [c.113]
Одно из основных следствий двухпериодной модели потребления состоит в том, что потребление домашнего хозяйства зависит не только от текущего дохода, но и от дохода, который ожидается в будущем. Точнее, потребление в каждом году должно зависеть от среднего уровня дохода, ожидаемого в этом году и в следующие годы. Это основное положение было впервые сформулировано в 1950 г. лауреатом Нобелевской премии экономистом Милтоном Фридменом. Он использовал термин "перманентный доход", чтобы обозначить средний доход, который домашнее хозяйство ожидает получать в долгосрочной перспективе. Модель перманентного (постоянного) дохода была впервые представлена в 1957 г. в классическом исследовании Фридмена "Теория функции потребления"8. [c.117]
Более высокие налоги сокращают потребление при заданной траектории выпусков, так как сокращается дисконтированная величина располагаемого дохода, доступного домашнему хозяйству 16. Влияние повышения налогов Т на С,, конечно, зависит от того, является ли оно временным или перманентным (в случае двухпериодной модели — относится ли это к обоим периодам или только к одному из них). Временное повыше- [c.124]
Заметим, что в жизни каждого человека есть два периода с "отрицательной" динамикой сбережений молодые годы и старость. Рис. 4-66 представляет ту же самую идею в уже знакомой нам форме двухпериодной модели. Если мы будем считать, что первый период — это годы труда, а второй — годы, прожитые после ухода на пенсию, то мы придем к тем же выводам. (К сожалению, двухмерный график не позволяет изобразить ранний период жизни.) Люди накапливают сбережения во время периода занятости, чтобы обеспечить дополнительный доход в старости, поскольку их доход в первом периоде выше, чем во втором. (Другими словами, их доход в первом периоде превышает перманентный доход.) [c.126]
Исследуя эту проблему, мы вновь обратимся к двухпериодной модели. Допустим, что помимо своего выпуска Q. и Q2 в каждом периоде домашнее хозяйство получает также дивиденды 2) К, и DV2 от своей собственной фирмы. Фирма получает прибыль /V, и Рг2 и выплачивает ее часть в качестве дивидендов. Фирма может принять решение удержать часть прибыли в первом периоде и вложить ее в покупку государственных облигаций Bj в соответствии со следующим бюджетным ограничением Вд = Рг — - DVV Сбережения фирмы определяются как удержанная прибыль, поэтому S = В = /V, — DVr Во втором периоде фирма не видит смысла в том, чтобы удерживать доходы, поэтому она выплачивает домашнему хозяйству всю прибыль второго периода плюс стоимость облигаций и начисленный на них процент DV2 = Рг2 + (1 + r)Bfl. [c.137]
Двухпериодная модель, делящая срок жизни домохозяйства на две части — настоящее и будущее, значительно упрощает исследование выбора многопериодной траектории потребления. Эта модель позволяет нам с помощью несложного графика найти точку равновесного потребления наложением кривых безразличия на многопериодное бюджетное ограничение. [c.139]
В рамках двухпериодной модели рассмотрим два домашних хозяйства, которые получают одинаковый доход в каждом периоде. Однако из-за различных предпочтений первое домашнее хозяйство сберегает 100 долл. в год, а второе — 1000 долл. в год. Какое из этих домашних хозяйств быстрее увеличит свои сбережения с ростом ставки процента Почему [c.141]
Как изменятся потребление и личные сбережения в первом и втором периоде в рамках двухпериодной модели, если [c.142]
Вернемся к нашей базовой двухпериодной модели и воспользуемся производственной функцией. Теперь любое домашнее хозяйство располагает двумя способами распределения во времени покупательной способности оно может взять деньги в долг на финансовых рынках под процент г или делать инвестиции для увеличения объема выпуска в будущем. В двухпериодной модели это можно выразить следующим образом (если предположить, как обычно, что домашнее хозяйство вначале не имеет никаких облигаций В) [c.152]
Равновесное состояние, описываемое соотношением (5.8), является, по существу, особым случаем в рамках двухпериодной модели. В этой модели [c.154]
Доказательство данного положения в рамках двухпериодной модели приведено в приложении к данной главе, однако его значение мы рассмотрим здесь. В современном обществе владельцами крупных фирм обычно являются тысячи индивидуальных инвесторов, каждому из которых в фирме принадлежит своя доля. Как же фирме принимать решения о величине инвестиций, если у каждого акционера свои динамические предпочтения Суть дела в том, что фирме не следует обращать на это внимание. Управляющие фирмой должны просто стремиться к максимизации ее рыночной стоимости, а это само по себе обеспечит максимизацию богатства акционеров. Таким образом, именно акционеры решают, как распределить во времени имеющееся богатство путем принятия индивидуальных решений относительно займов и кредитования. [c.157]
Предположим, что в двухпериодной модели инвестиций производственная функция описывается выражением Q = 2А1/2, первоначальный основной (наличный) капитал К = 81, ставка процента составляет 11% [c.175]
Проанализируем двухпериодную модель, согласно которой домашние хозяйства и фирмы являются самостоятельными экономическими единицами, а последние принимают инвестиционные решения. Используя труд и капитал, фирма обеспечивает выпуск (0. В краткосрочной перспективе ее прибыли равны объему выпуска минус расходы на оплату труда. Обозначим заработную плату через w, а объем используемого в производстве труда — через L. Тогда прибыль (Рг) в периоды 1 и 2 составит [c.177]
Многопериодное бюджетное ограничение в двухпериодной модели [c.198]
Многопериодное бюджетное ограничение страны можно исследовать формально с помощью двухпериодной модели. Предположим, как ранее мы делали при рассмотрении домашнего хозяйства, что страна начинает движение с нулевыми зарубежными активами (ffQ = 0). В этом случае величина В в первом периоде (5, ) будет равна активному сальдо счета текущих операций в первом периоде [c.198]
Однако в соответствии с построением двухпериодной модели страна должна прийти к концу второго периода с нулевыми зарубежными активами (5 = 0), а во втором периоде она не делает инвестиции (/2 = 0). Поэтому, объединив соотношения (6.15) и (6.16), получим [c.198]
Бухгалтерский учет применительно к платежному балансу в двухпериодной модели [c.201]
Двухпериодную модель можно расширить на любое число периодов. При этом коэффициенты и и d, а также ставка процента г могут меняться от периода к периоду. Хотя на каждом шаге цена акции может принимать лищь два значения, при большом числе периодов можно аппроксимировать достаточно плавно изменяющуюся цену. Например, если опционы исполняются в конце торгового дня, "периодом" можно считать один час (соответственно подобрав величины u, d и г). Если до конца дня остается 7 часов, то финальная цена акции, в соответствии с многопериодной биномиальной моделью, может иметь 27 = 128 значений. [c.90]
Теперь допустим, что домохозяйство функционирует в так называемой двухпериодной модели первый период — "настоящее" с параметрами QJ, С1 S Blf второй период — "будущее" с параметрами Q2, С2, S2, B2. Далее предположим, что сбережения первого периода (S = Bj) равны "антисбережениям" второго периода (S2 = В2), т. е. во втором периоде домохозяйство потратило на потребление то, что оно сберегло в первом периоде (Sl = S2). Но, поскольку S = Y — С, получится [c.448]
Заметим, что мы рассмотрели весьма упрощенную иллюстрацию эквивалентности Барро-Рикардо для двухпериодной модели. В действительности, ни государство, ни домохозяйства не руководствуются каким-то конкретным временным горизонтом, и правильным было бы продемонстрировать, что результат имеет место в модели с бесконечным горизонтом времени. В этом случае снижение налогов в первом периоде и увеличение на соответствующую величину государственного долга может не сопровождаться выплатой долга и, соответственно, резким повышением налогов в следующем периоде. Скорее следует ожидать, что выплата долга растянется на много лет, а, значит, и налоги будут увеличены на меньшую величину, но это повышение коснется целого ряда периодов. Более того, можно рассмотреть ситуацию, когда выплата долга растянется на бесконечное число периодов. Очевидно, что в [c.103]
Рассмотрим следующую двухпериодную модель торга. В первом периоде г> и с не известны ни той, но другой стороне — они симметрично неинформированы и знают только рас- [c.453]
Продолжим наше обсуждение, используя формальную модель в случае, когда домашнее хозяйство функционирует в течение двух периодов. Не обязательно, чтобы эти периоды были одинаковыми по продолжительности. Можно представить себе первый период как "настоящее", а второй — как "будущее". (Удобно также считать нулевой период "прошлым".) Пока мы изучаем эту проблему на абстрактном уровне, неважно, сколько лет длится каждый период. Эта упрощенная постановка, известная как двухпериодная модель, отражает все важные аспекты принятия решений с учетом фактора времени и при этом довольно удобна. (Когда мы перейдем к эмпирическим исследованиям, мы обратимся к более реалистичным многопериод-ным моделям.) [c.111]
