Точность определения полного приращения функции А/ при использовании дифференциального метода возрастает с увеличе- [c.91]
Полное приращение функции 136 [c.329]
Полным приращением Az функции [c.288]
Пусть функция f(M) определена га некоторой окрест ности точки Af0( . .. х°с ХИЛ- Рассмотрим точку /Ид (х° + Лжх . . . л + А, - . . . нь х ). Полным приращением Д/ функции /(М) в точке -/И называется число /(МД)-/(М0), т. е. [c.136]
Функция полезности — это способ приведения предпочтений инвестора к одному показателю, который называется полезностью , на основе некоторых переменных выбора. Например, в данном случае полезность, или удовлетворенность, инвестора определяются как функция богатства. Приняв данное положение, мы сумеем успешно ответить на следующие вопросы. Станут ли инвесторы в два раза счастливее, если их богатство увеличится в два раза Приводит ли каждое маргинальное приращение богатства к меньшему приросту полезности, чем предыдущее приращение В том случае, когда функция полезности принимает специфическую форму (а именно форму квадратичной функции), то полную полезность инвестора можно выразить в виде ожидаемого богатства и стандартного отклонения в данном богатстве. [c.86]
| Таблица 3.1 Поправка за нормальное приращение в функции выноса х и полного вертикального времени для данной скоростной функции. | 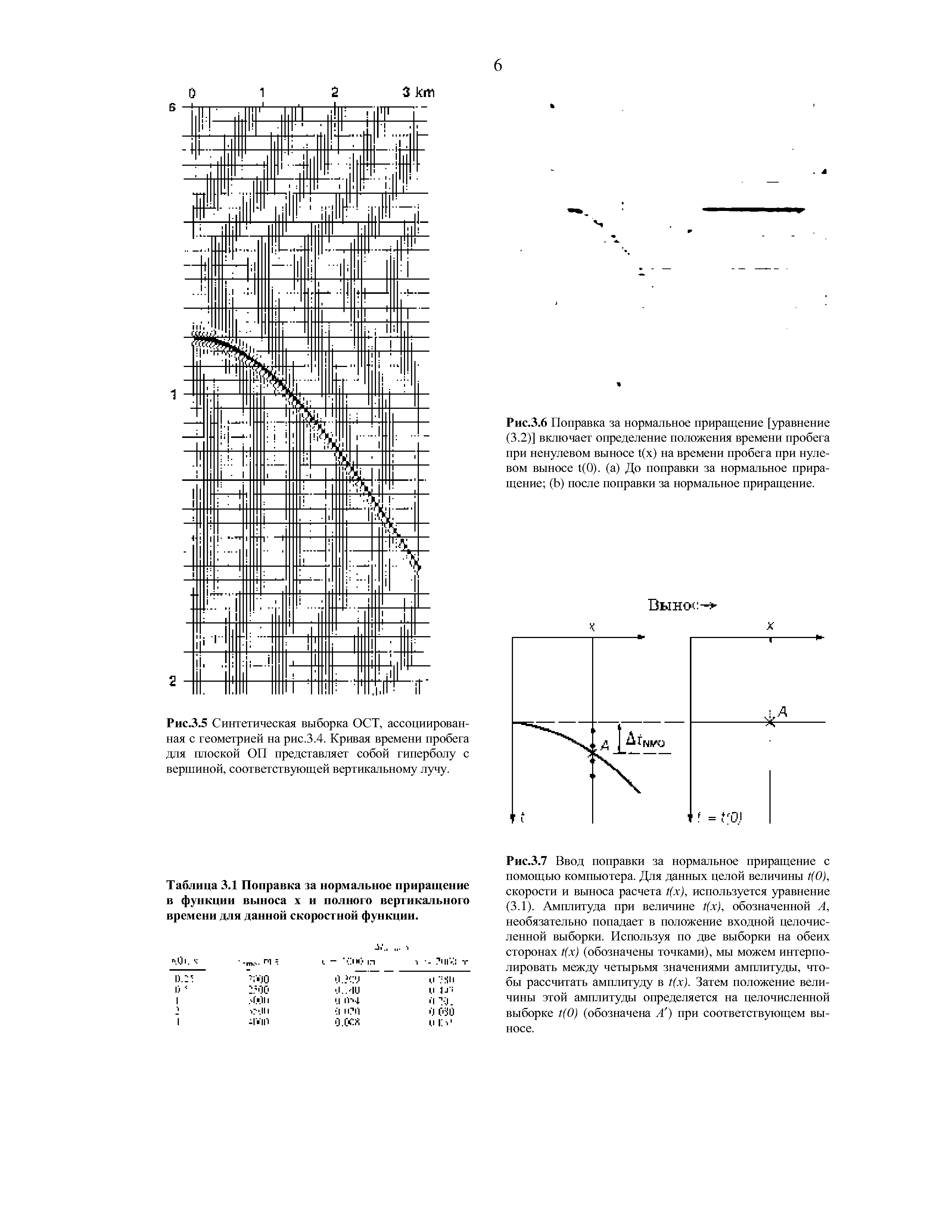 |
Пусть функция /(М) определеша в некоторой окрестности точки М , М0 R"- Функщиш / (М) называется дифференцируемой в точке М0, еслш полное приращение А/ в этой точке имеет следующий вид. [c.136]
Пусть в момент t=0 полная энергия ЩО) системы (1.1) равна Ео<Етах. Поставим следующую задачу. Найти управления Uj(q,p), i=l,...,n, как функции от состояния системы (1.1), удовлетворяющие указанным ограничениям, при которых скорость изменения энергии dE(t)/dt в каждый момент t для кусочно-непрерывных управлений или величина приращения энергии ДЕ(т) за каждый интервал Im, m=0,l,2,..., для импульсных управлений максимальна по абсолютной величине. [c.8]
