Центробежно-струйные форсунки отличаются от центробежных наличием двух потоков, на которые разделяется подводимая жидкость, взаимодействующих в камере смешения. Первому, периферийному, сообщается вращение, а второй подается в камеру смешения в виде осевой струи. Вращающийся поток передает часть энергии центральной струе и частично раскручивает ее, а сам несколько тормозится. В результате образуется единый результирующий поток, который за пределами соплового канала разрушается с образованием факела в виде заполненного конуса. [c.71]
РАСПИЛИВАНИЕ ЖИДКОСТЕЙ ЦЕНТРОБЕЖНО-СТРУЙНЫМИ ФОРСУНКАМИ [c.106]
В центробежно-струйной форсунке (на рис. 5.1 в качестве примера приведена форсунка с цилиндрическим вкладышем) жидкость, как уже отмечалось, разделяется на два потока [c.106]
| Рис., 5.1. Схема центробежно-струйной форсунки с цилиндрическим вкладышем |  |
Проводя аналогию между рассматриваемым течением газовых потоков и смешением потоков в центробежно-струйной форсунке, можно ожидать, что и в нашем случае распределение аксиальной составляющей скорости. w x с достаточной степенью точности будет равномерным. Распределение тангенциальной составляющей в сопловом канале w
[c.110]
Таким образом, в качестве основных предпосылок для теоретического описания протекающих в центробежно-струйной форсунке процессов можно принять следующие предположения
[c.110]
Пол-агая здесь ф=1, получим условие сплошного заполнения соплового канала центробежно-струйной форсунки А Кр=1.
[c.113]
АНАЛИЗ ХАРАКТЕРИСТИК ЦЕНТРОБЕЖНО-СТРУЙНОЙ ФОРСУНКИ
[c.117]
Известны экспериментальные работы по исследованию влияния геометрических размеров центробежно-струйных форсунок на их характеристики [48, 119, 133]. Представляет несомненный интерес исследование этого влияния численным методом с помощью приведенной выше теории и сравнение результатов расчетов с экспериментальными данными.
[c.117]
Как показывают экспериментальные данные [44, 4 , Udj, корневой угол у всех центробежно-струйных форсунок при заполненном факеле не превышает 90°, а коэффициент расхода обычно больше 0,7. Следовательно, геометрический комплекс А в этих случаях меньше 1. Доля вращательной энергии в сопловом канале (а, следовательно, и А ) может быть увеличена за счет увеличения диаметра соплового канала d , среднего радиуса Яв и угла закручивания потока а. При этом благодаря увеличению внутреннего радиуса коаксиального вихря потоки в форсунке перестают взаимодействовать и истекают из нее раздельно. Увеличение размеров осевого канала с целью взаимодействия потоков снижает, как можно видеть из анализа выражения (5.14), долю вращательной энергии в сопловом канале. Таким образом, предельный корневой угол факела центробежно-струйных форсунок составляет 90°.
[c.119]
Значение комплекса А в центробежно-струйных форсунках изменяется в узком диапазоне —от 0 до 1. Значениям А >1
[c.119]
Как отмечалось выше, гидродинамическая модель центробежной форсунки является частным случаем предложенной модели центробежно-струйной форсунки. Приняв /0 = 0 в уравнении (5.14) (отсутствие осевого потока жидкости), получим выражение для геометрического комплекса А в виде
[c.120]
Взаимодействие потоков в камере смешения и сопловом канале центробежно-струйной форсунки исследовали путем окрашивания осевого потока (ввода трассера).
[c.124]
Рассмотренная теория центробежно-струйных форсунок позволяет рассчитать две основные характеристики распылителя коэффициент расхода и корневой угол факела.
[c.124]
В работе [127] авторы показали существование единых закономерностей работы центробежно-струйных форсунок, независимо от их конструктивного оформления. Экспериментальные исследования проведены на форсунке с цилиндрическим вкладышем (см. рис. 5.1), но полученные результаты могут быть распространены и на распылители других конструкций.
[c.124]
РАСЧЕТ ЦЕНТРОБЕЖНО-СТРУЙНЫХ ФОРСУНОК
[c.127]
Приведенные выше закономерности изменения плотности орошения по сечению факела центробежно-струйных форсунок показывают, что характер этих изменений достаточно сложен и является функцией большого числа переменных, которые /можно свести к двум обобщенным параметрам Ас и г ).
[c.128]
| Рис. 5.15. Блок-схема расчета центробежно-струйных форсунок. | 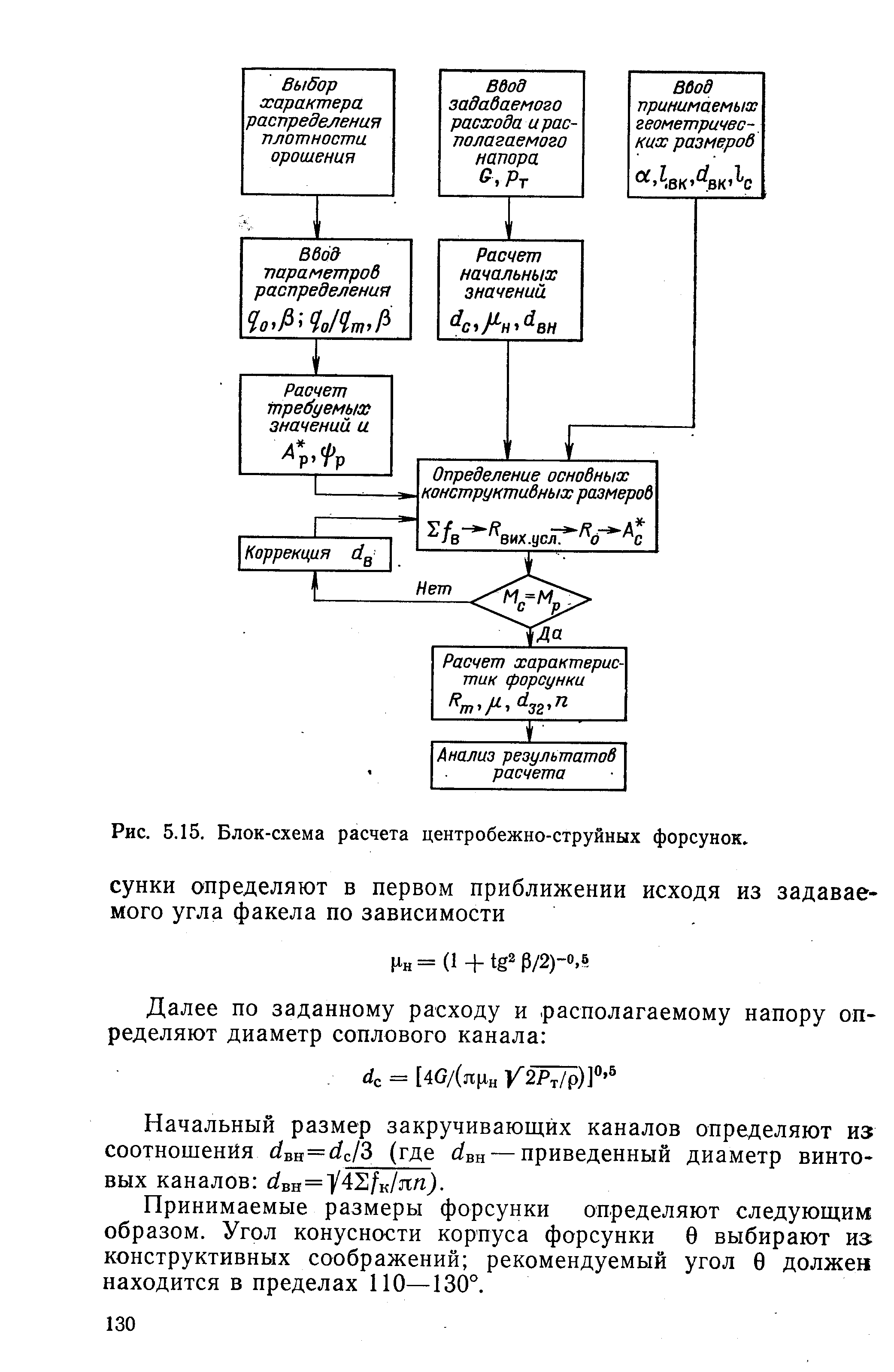 |
Блок-схемы расчета центробежно-струйных форсунок 129 ел. [c.249]
Форсунки комбинированные Коническая пленка 17 Концевой эффект 58 Корневой угол факела в акустических форсунках 190 схема расчета 9 в центробежно-струйной форсунке [c.250]
Согласно приведенной классификации [127], в основу которой положен принцип действия, различают струйные, с соударением струй, ударно-струйные, центробежные, центробежно-струйные и комбинированные форсунки. [c.71]
Ниже рассмотрены работа и конструкции форсунок пяти основных классов. Довольно подробно освещены наиболее распространенные в настоящее время центробежные форсунки. Особое внимание уделено центробежно-струйным форсункам. Учитывая их универсальность, возможность управления распределением плотности орошения, а также тот факт, что большинство из приведенных материалов обобщены впервые, авторы вынесли их в отдельную главу 5. [c.72]
Работ по исследованию распыления жидкости, вытекающей из кольцевого сопла струйных форсунок, практически нет. При малом среднем диаметре кольцевого канала и небольшой ширине его можно ожидать, что основные процессы будут аналогичны протекающим при распыливании жидкостей центробежными форсунками. [c.75]
Как отмечалось в главе 1, все многообразие возможных вариантов распределения жидкости в факеле форсунок можно свести к трем основным типам струйному, центробежному и центробежно-струйному (рис. 5.13, а—в). Для полного описания этих видов распределения предложены следующие параметры [119] q0 — относительная плотность орошения на оси факела qm — максимальная относительная плотность орошения,, достигаемая на периферии факела / т — относительный радиус факела, на котором достигается qm я —минимальная относительная плотность орошения между двумя максимумами Rn — относительный радиус, на котором достигается qn. [c.127]
На основе соотношений (5.17) и, (5.18), учитывая, что теорети ческий расход 0=1фсУ2Рж/р, можно показать, что коэффициент расхода центробежно-струйной форсунки равен [c.113]
Это выражение отличается от полученного в работе [1] множителем 2. Иными являются и зависимости для коэффициента расхода и и корневого угла факела р. Эти различия обусловлены тем, что. при выводе теории центробежно-струйной форсунки мы пользовались линейной зависимостью для тангенци-альйой составляющей скорости жидкостного потока в сопловом канале, а в работе [1] для центробежной форсунки был принят гиперболический профиль скорости. [c.120]
Сравнение полученного математического описания центро-бежно-струйной форсунки с теорией, приведенной в работе [1], показывает, что оно с достаточной степенью точности может быть использовано и для расчета центробежных форсунок, т. е. теория центробежных форсунок является частным случаем предложенной математической модели центробежно-струйной форсунки. [c.121]
Как можно видеть из представленных на рис. 5.8 зависимостей, несмотря на различный характер распределения жидкости в факеле, происходит взаимное смешение (проникновение) потоков в камере смешения и сопловом канале центробежно-струйной форсунки, о чем говорит выравнивание относительной концентрации трассера ( OT = i/ m) по сечению сопла. Вместе с тем для различных распределений q наблюдаются и отличия в распределении Сот, обусловленные степенью взаимодействия потоков гр. Так, при достаточно высокой интенсивности взаимодействия, т. е. при центробежном (кривая q на рис. 5.8, а) или струйном (кривая qz на рис. 5.8, а) распределении, происходит почти полное выравнивание концентрации трассера по сечению сопла. На границе факела она до- стигает 0,95—0,97 от Стах. [c.124]
Учитывая возможности форсунок этого класса, авторы поставили перед собой более сложную задачу разработать методику расче-та центробежно-струйных форсунок, которая учитывала, бы и задаваемый характер распределения плотности орошения по сечению факела. Решить ее аналитически, т. е. найти взаимосвязь геометрических размеров форсунки и распределения плотности орошения, очень сложно, поэтому был выбран эмпирический путь. [c.124]
Как отмечалось, в число исходных данных должны быть включены и дисперсные характеристики. Для вывода расчетных уравнений известные экспериментальные данные, а также данные, полученные авторами, обработаны в виде критериаль-ных уравнений, в которых в качестве геометрического критерия подобия принята геометрическая характеристика центробежно-струйных форсунок А [c.129]
В литературе описано более трех десятков конструктивных схем центробежно-струйных форсунок. Все их можно разделить на три большие группы с тангенциальным вводом периферийного потока в камеру закручивания, с завихряющими вкладышами и шнеками и форсунки, в которых осевой поток жидкости формируется с помощью специальных конструктивных элементов. [c.132]
| Рис. 9.12. Схемы пульсационно-гидравлических центробежно-струйных форсунок | 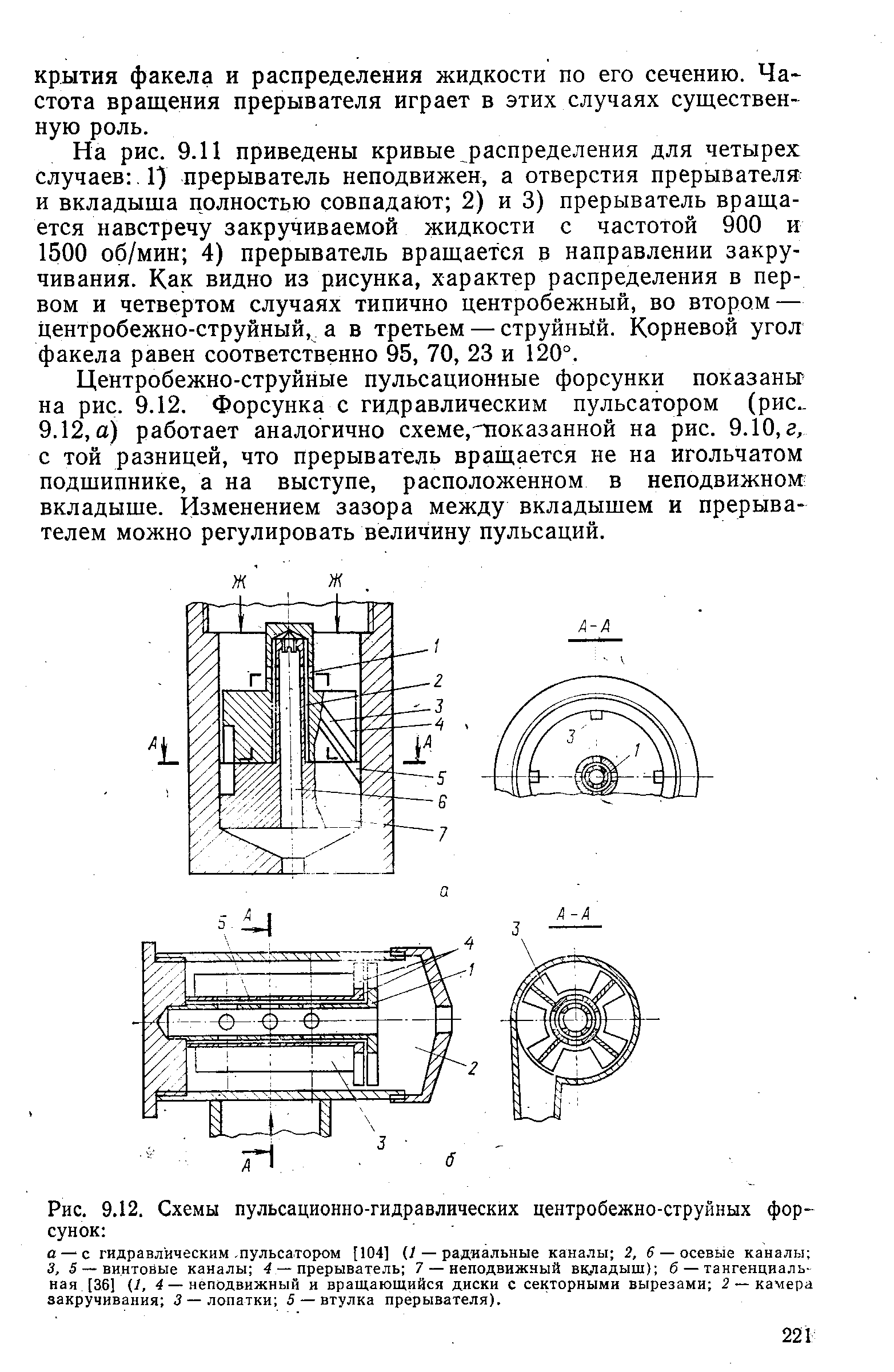 |
Центробежно-струйные форсунки см. Форсунки центро бежно-струйные [c.254]
Коэффициент неравномерности в значительной мере определяется и характером распределения плотности орошения по сечению факела. Из всего многообразия встречающихся распределений плотности можно выделить три типичных вида (см. рис. 5.13). Распределение, в котором q максимально на оси и монотонно убывает к периферии факела, характерно для факелов, образующихся при разрушении сплошных струй, поэтому будем называть его струйным. Распределение, при котором q имеет провал на оси, затем возрастает до максимума и после этого монотонно убывает, впервые наблюдалось при распаде полой конической пленки, образующейся вследствие закручивания жидкости в распылителе. Назовем это распределение центробежным, поскольку оно наблюдается в центробежных форсунках. Все промежуточные варианты распределений плотности орошения назовем центробежно-струйным, поскольку (как будет показано ниже) они характерны для цёнтробежно-струй-ных форсунок. [c.9]
Исследована [120] работа центробежно-струйных пульсаци-онных форсунок с прерывателем, имеющим механический привод (рис. 9.8,а) и с возбудителем.- поршневым пульсатором давления (рис. 9.8,6). Частота пульсаций изменялась от 5 до 250 Гц, перепад давления — от 0 до 1,2 МПа. [c.216]
Центробежно-струйные пульсационные форсунки показаны на рис. 9.12. Форсунка с гидравлическим пульсатором (рис.. 9.12,а) работает аналогично схеме.тюказанной на рис. 9.10,г, с той разницей, что прерыватель вращается не на игольчатом подшипнике, а на выступе, расположенном в неподвижном вкладыше. Изменением зазора между вкладышем и прерывателем можно регулировать величину пульсаций. [c.221]
