Модель переменного роста [c.554]
При определении курса обыкновенной акции с помощью модели переменного роста требуется вычислить приведенную стоимость прогнозируемого потока дивидендов. Это можно сделать следующим образом разделить общий поток на две части, рассчитать приведенную стоимость каждой части и затем сложить их вместе. [c.555]
Процедура оценки для модели переменного роста, задаваемая равенством (18.27), проиллюстрирована на рис. 18.1. [c.556]
Теперь мы можем показать, что модель постоянного роста является частным случаем модели переменного роста. В частности, если предположить, что момент времени, с которого должен начаться постоянный рост, равен нулю, то [c.557]
Ранее отмечалось, что наиболее общая DDM — это модель переменного роста, в которой предполагается, что дивиденды растут с переменным темпом роста до некоторого периода времени Т в будущем, после чего они увеличиваются с постоянным темпом роста. В этом случае приведенная стоимость всех дивидендов определяется путем сложения приведенных стоимостей дивидендов до периода Г включительно (Vr) и приведенных стоимостей всех дивидендов после периода Т (V ) [c.563]
Заменяя числитель в равенстве (18.37) правой частью равенства ( 1 8.45) и затем деля обе части на Е0, получим следующую формулу определения нормального отношения цена—доход в рамках модели переменного роста [c.563]
| Рис. 18,3. Три стадии в модели переменного роста | 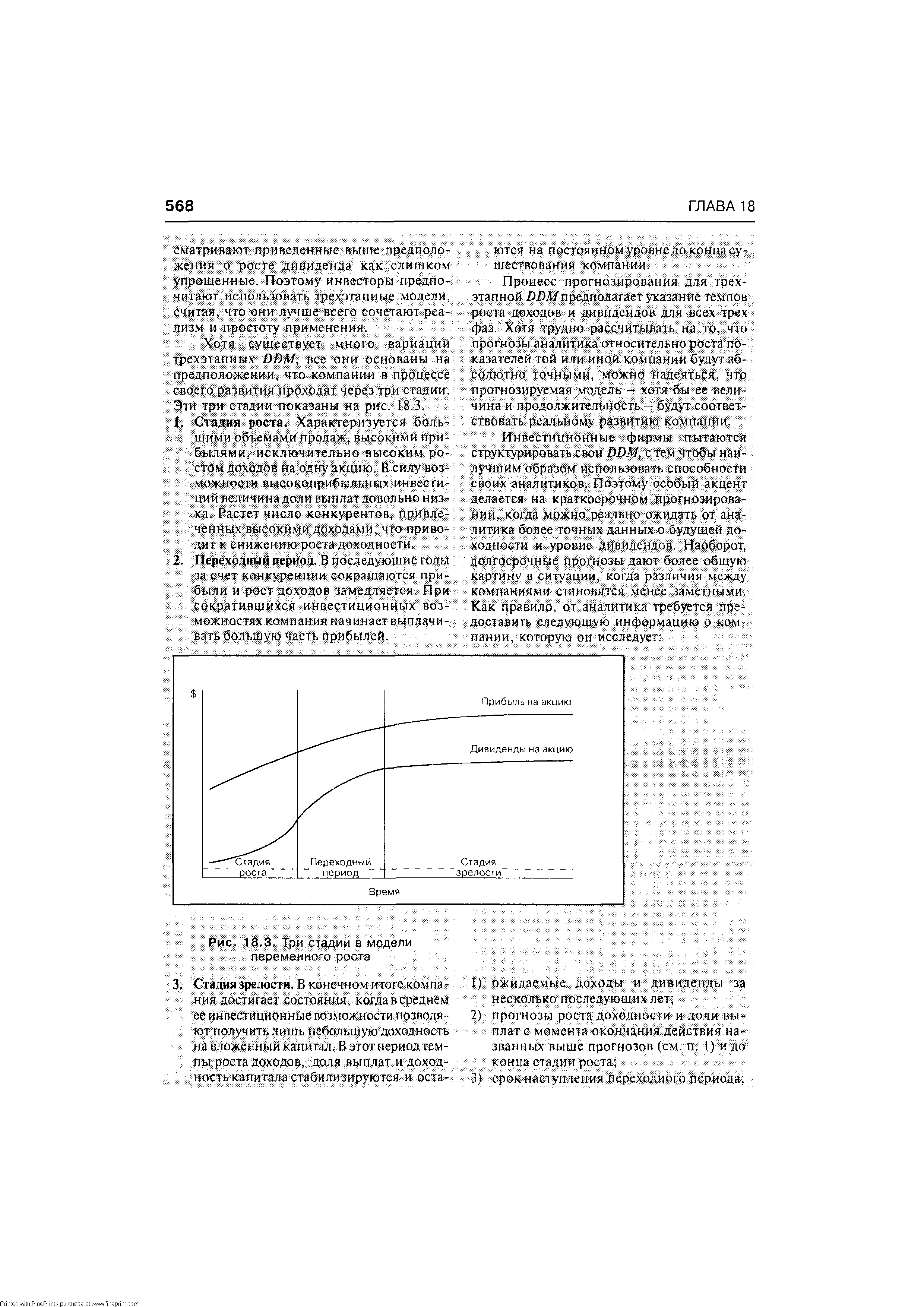 |
Третье предположение описывается с помощью модели переменного роста. Главная особенность этой модели — период времени в будущем (Т), после которого ожидается, что дивиденды будут расти с постоянным темпом (g). При этом необходимо составить прогноз дивидендов до периода Т исходя из индивидуального прогноза по величине дивидендов для каждого подпериода, а также рассчитать наступление момента Т. После наступления момента Т дивиденды будут расти следующим образом [c.355]
Модель переменного роста.....................................................................554 [c.1019]
Модель переменного роста.......................................................563 [c.1019]
| Рис. 18.1. Временная линия для модели с переменным ростом |  |
С помощью эконометрических моделей связывают размеры продаж с макроэкономическими переменными (ростом ВНП, колебания учетной ставки и т. д.), а также с отраслевыми данными (например, емкость отраслевого рынка, уровень конкуренции). [c.131]
| Таблица П9. Модель правила денежно-кредитной политики, оцененной GMM (инструмент — денежная база, целевая переменная роста экономики — ВВП), с корректированной автокорреляцией ошибок |  |
В моделях нулевого и постоянного роста равенство для Кможет быть переписано таким образом, чтобы можно было вычислить внутреннюю ставку доходности по инвестициям в данный вид акций. К сожалению, для модели переменного роста удобных формул, наподобие равенств (18.15а), (18.156), (I8.23a) и (18.236), не существует. Это очевидно, так как выражение для IRR получается, если в уравнении (18.27) заменить V на Р и k на k [c.556]
Инвесторы также применяют две модели дисконтирования дивиденда, получившие названия двухэтапной и трехэтапной моделей5. Двухэтапная модель предполагает, что до некоторого момента времени существует одна постоянная ставка роста gt, затем устанавливается другая ставка, равная gr Трехэтапная модель предполагает, что одна постоянная ставка gl действует до некоторого времени Г,, затем начинает действовать вторая ставка до времени Т2, а после этого действует третья ставка. Обозначая через У. приведенную стоимость дивидендов после того, как стала действовать последняя ставка, а через Ут приведенную стоимость всех остальных предшествующих дивидендов, получим, что обе эти модели являются частными случаями модели переменного роста. [c.557]
Но не все потеряно. Остается возможность вычисления /ЛЛдля модели с переменным ростом путем простого подбора значений. Правая часть равенства (18.28) равна приведенной стоимости потока дивидендов, для которого k используется в качестве ставки дисконтирования. Отсюда, чем больше значение k, тем меньше значение правой части уравнения (18.28). Подбор начинается с какого-либо начального приближения для k. Если соответствующее значение правой части уравнения (18.28) больше Р, то затем подставляется большее значение k. Наоборот, если полученное значение меньше Р, то подставляется меньшее значение k. Продолжая эту процедуру далее, инвестор в [c.556]
Предмет и метод макроэкономического анализа макроэкономические показатели и способы их измерения. Экономика в долгосрочной перспективе. Теории и модели экономического роста. Экономический рост и его детерминанты. Первые теории экономического роста предшественники современных моделей (физиократы классики, Рикардо и Маркс). Математические модели экономической динамики. Динамическая модель В.Леонтьева. Модели расширяющейся экономики Неймана-Гейла. Технологический и экономический темпы роста. Траектории сбалансированного роста. Теоремы о магистрали. Неоклассическая модель экономического роста Солоу-Свана. Проблемы интерпретации переменных модели и объяснения исторических и межстрановых различий в уровне дохода. Современные модели экзогенного и эндогенного роста. Модели и теории безработицы, естественный уровень безработицы, причины безработицы. Теории и модели инфляционных процессов, количественная теория денег инфляция и инфляционный налог, причины и издержки инфляции. [c.128]
В отличие от Ladron-de-Guevara et al. (1999), мы делаем акцент на сравнении двух качественно различных режимов роста эндогенного и экзогенного, соответствующих внутреннему и краевому решению. Это необходимо для выявления условий интеграции неоднородных экономик. Мы опираемся на сравнительно простой вариант модели эндогенного роста с переменной свободного времени, но пытаемся развить ее в двух направлениях. С одной стороны, предлагается анализ экзогенной траектории роста, а также развивается исследо- [c.8]
