Конечно, в задачах, встречающихся в практических исследованиях, сети бывают значительно сложнее, так что для расчета требуется провести значительное число описанных здесь шагов. Тем не менее во многих случаях с помощью метода потенциалов удалось решить практические задачи даже без использования ЭВМ. По своему смыслу потенциалы близки к двойственным переменным соответствующей задачи линейного программирования в матричной постановке (см., например, [13]). [c.191]
Расчеты сетевых графиков по методу потенциалов [c.90]
Метод потенциалов относится к графическим способам расчета сетевых графиков. Потенциалом события называется продолжительность максимального завершающего пути (пути от данного события до завершающего). Потенциал завершающего события сетевого графика равен нулю. Потенциалы остальных событий находятся по величине потенциалов последующих событий работ сетевого графика по формуле [c.90]
Например, в рассмотренном ранее примере сетевого графика (рис. 20) общий резерв времени работы 2-5 по методу потенциалов равен (20 - 7) - (8 + 3) = 2, частный резерв этой работы -13 - (8 + 3) = 2. По работе 3-7 по методу потенциалов общий резерв равен (20 -4) - (10 + 2) = 4, частный резерв - 12 - (10 + 2) = 0, что совпадает с результатами секторного и табличного способов расчета. [c.91]
В настоящее время разработано множество различных алгоритмов решения Т.з. распределительный метод, метод потенциалов, дельта-метод, венгерский метод, метод дифференциальных рент, способ двойного предпочтения, различные сетевые методы. Они относительно просты, по ним составлены десятки программ для различных вычислительных машин. Во многих снабженческих, транспортных и других организациях во всем мире с их помощью рассчитываются маршруты доставки материалов на строительные площадки, планы длительного прикрепления поставщиков металлопроката к потребителям, планы перевозок топлива. Задачи эти часто усложняются разного рода дополнительными условиями напр., в них включается расчет не только себестоимости перевозок, но и себестоимости производства продукции (производственно-транспортная задача), оптимизируется совместно доставка взаимозаменяемых видов продукции (скажем, различных кровельных материалов), оптимизируется доставка грузов с промежуточными базами (складами). Кроме того, следует учитывать, что экономико-математическая модель Т.з. позволяет описывать множество ситуаций, весьма далеких от проблемы перевозок, в частности, находить оптимальное размещение заказов на производство изделий с разной себестоимостью. [c.367]
После построения экономико-математической модели решается задача прикрепления поставщиков к потребителям. Расчеты выполняют в специальной таблице (матрице) линейного программирования методом потенциалов (табл. 4.19). В этой таблице, кроме ресурсов поставщиков, потребностей потребителей и транспортных расходов, имеются столбец и строка для записи потенциалов /, и Uj, которые дают возможность определить оптимальность плана закрепления поставщиков за потребителями. [c.153]
Известны различные способы решения этой задачи - распределительный, венгерский, метод потенциалов и др. Как правило, для расчетов применяется ЭВМ. [c.11]
Оказывается, для того, чтобы решить маршрутную задачу с помощью транспортной модели, нужно принять в качестве однородного груза... пустые вагоны, направляемые от пункта выгрузки к пунктам погрузки. Полученное распределение, которое без труда находится на основе транспортной задачи, и дает решение задачи об оптимальной маршрутизации, так как оно определяет пути следования вагонов. Практическое применение транспортной задачи для решения задач оптимальной маршрутизации получило особенное распространение на автотранспорте. В ряде крупных городов производится ежедневный расчет рациональных маршрутов на ЭВМ и на их основе пишутся наряды для значительного процента автомашин. В некоторых небольших автохозяйствах эту методику хорошо освоили и регулярно используют сами диспетчеры. Это позволяет в ряде случаев снижать холостой пробег на 20—40%. Об эффекте ее применения убедительно свидетельствует и такой любопытный факт. В одном автохозяйстве, где проводился эксперимент по введению наилучшей маршрутизации транспорта, шоферы, ездившие по оптимальным маршрутам, найденным с помощью метода. потенциалов, имели на своих машинах отличительные флажки. Через несколько дней после начала эксперимента шоферы наглухо припаяли флажки к машинам, так как они стремились и впредь получать математические наряды. Большая эффективность работы этих машин была выгодна не только для автохозяйства в целом, но и для каждого и,з водителей. [c.43]
| Рис. . Расчет сете ого графике методом потенциалов | 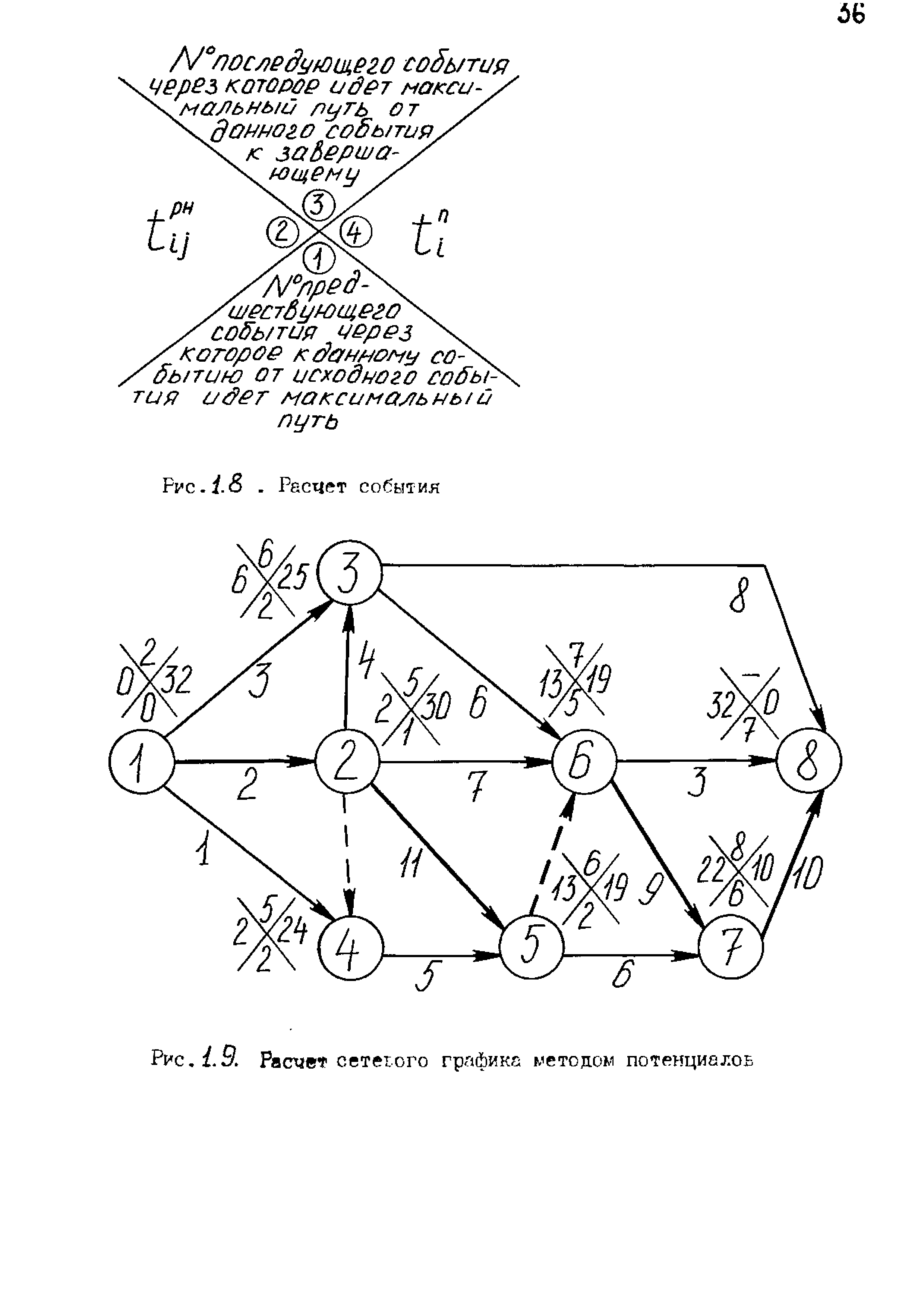 |
Изменения продолжительностей работ, возникающие в ходе выполнения графика, не влияют на потенциал последующих событий, поэтому пересчет графика занимает мало времени. Ускоренный расчет сетевых графиков методом потенциалов удобен для анализа хода строительства без применения ЭВМ. [c.38]
За последние годы произведено техническое перевооружение электроразведки. Для исследования геологического разреза на большие глубины методами постоянного тока применяются электроразведочные станции с мощными генераторами и осциллографами для регистрации измеряемой разности потенциалов. Эти станции обеспечивают повышение качества работ, сокращают затраты труда и материальных средств в расчете на 1 км2 исследуемой площади. [c.83]
Вопрос о знаке, с которым входит Gkk и Gkm в матрицу для расчета по методу узловых потенциалов может быть решен на основании следующих условий [c.157]
За последнее десятилетие в энергетике сложились различные системы экономического стимулирования энергоремонтного производства. Они отличаются друг от друга по следующим основным характерным чертам системе используемых экономических показателей методам формирования поощрительных фондов уровню хозяйственной ответственности за результаты работы уровню развития хозяйственного расчета способу расчетов (с заказчиками) за выполненные работы стимулирующему потенциалу. [c.325]
Аналогично разрабатывают и матрицы для расчета плана по труду и заработной плате, себестоимости и фондам экономического стимулирования. В плане перевозок матричный метод использован для распределения транспортной работы по маркам подвижного состава с учетом их рентабельности. Матрицы решают с помощью математического метода МОДИ или метода потенциалов. [c.18]
Помимо алгоритма метода потенциалов существуют некоторые его разновидности. Так, в иностранной литературе как указано выше, широко известен метод МОДИ (модифицированный распределительный метод). В СССР этот метод многие экономисты именуют методом коэффициентов. Отличие этого метода заключается в способе расчета коэффициентов. [c.218]
Смотреть главы в:
Организация и экономика строительного производства -> Расчет методом потенциалов
