| Рис.4.1 Переходы между состояниями марковской цепи эволюции макросреды Распределение переходных вероятностей на различных временных срезах характеризует уровень доверия эксперта к экономическим действиям существующего и будущих правительств. Оценки эксперта позволяют построить марковский прогноз развития экономической ситуации. Иллюстративный прогноз на 2001-2005 гг. в предположении, что в настоящее время Россия испытывает период стагнации, представлен в табл. 4.2. В последней графе приведено стационарное распределение марковской цепи, которое практически достигается уже через 6 лет. Из прогноза видно, что, если так пойдет и впредь, то вероятность кризисов и периодов быстрого роста достаточно велика и ее нельзя сбрасывать со счетов. Отметим, что даже в столь простом случае цепь содержит 55=3125 различных траекторий, то есть сценариев, каждый из которых имеет вероятность реализации, не превышающую 0,00032. | 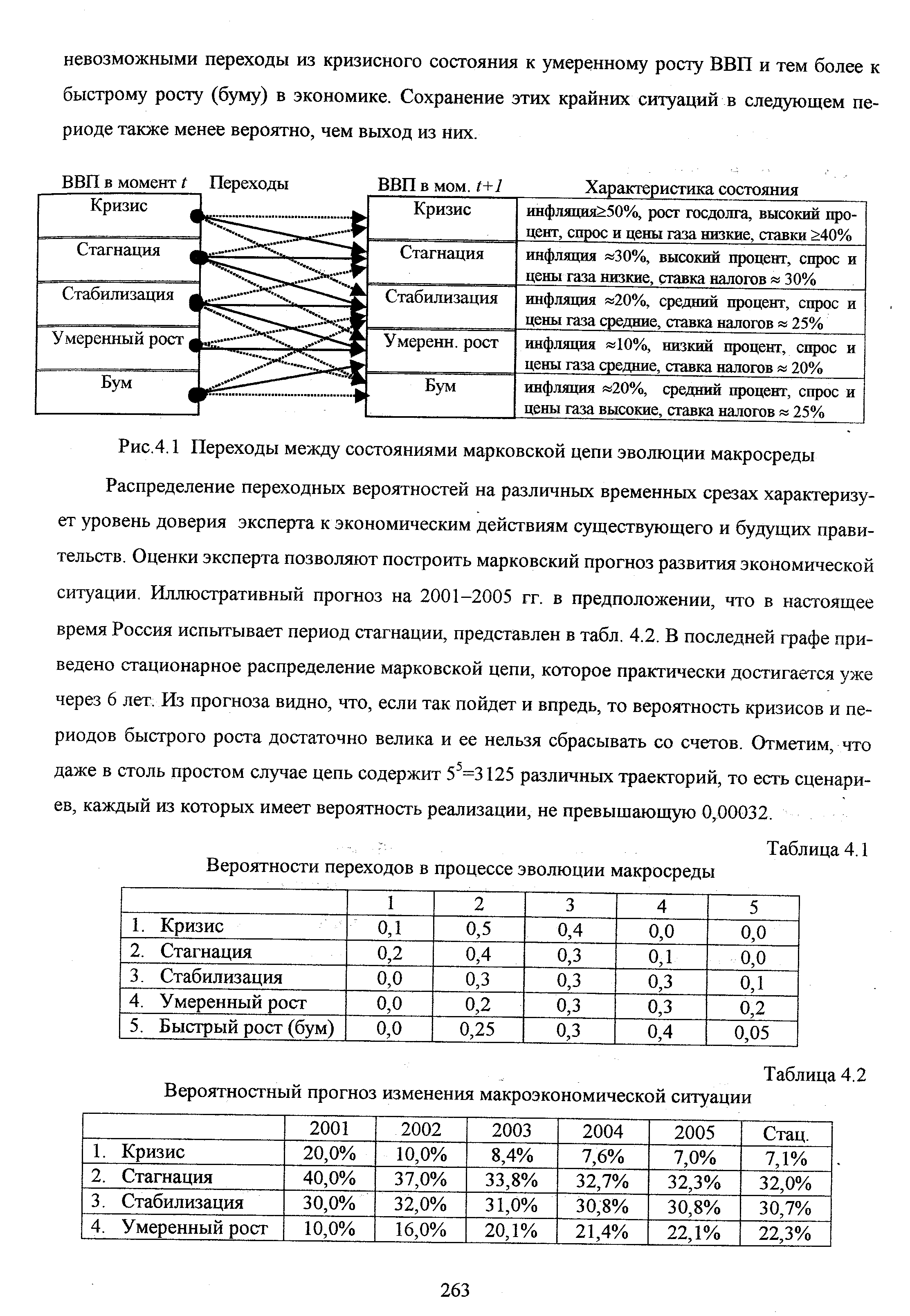 |
Можно считать, что события, переводящие автомобиль из состояния в состояние, представляют собой потоки событий (например, потоки отказов). Если все потоки событий, переводящие систему (автомобиль) из состояния в состояние, пуассоновские (стационарные или нестационарные), то процесс, протекающий в системе, будет марковским, а плотности вероятности перехода Ху в непрерывной цепи Маркова представляют собой интенсивности потока событий, переводящего систему из состояния Si в состояние Sj. Например, Х03 - интенсивность потока отказов автомобиля, который переводит автомобиль из состояния исправен, работает в состояние находится в ТР . [c.63]
С течением времени в такой системе устанавливается предельный стационарный режим, в ходе которого она переходит из одного состояния в другое состояние, но вероятности состояний уже не меняются. В этом предельном режиме каждая финальная [c.157]
В данном параграфе устанавливается связь между пуассоновскими потоками событий и дискретными марковскими процессами с непрерывным временем. Показывается, как используется интенсивность пуассоновских стационарных потоков в качестве плотностей вероятностей переходов системы из состояния в состояние при анализе моделей конкретных ситуаций. [c.123]
Свяжем немарковские переходы с моментами регенерации вложенной цепи, для которых рассчитываются тг . Параметр А/,, марковских переходов (прибытие новых заявок) при наличии в системе ровно k заявок может быть отнесен к произвольному моменту и должен связываться со стационарной вероятностью р . Баланс переходов между смежными состояниями системы в стационарном режиме требует равенства [c.286]
Здесь отметим, что если производственная система рассматривается в стационарном режиме, то задача (ПЛ)-(И.б) сводится к задаче линейного программирования. В ряде случаев ограничения (11.2)-(11.6) могут быть также представлены выражениями, описывающими и вероятности перехода системы из состояния в состояние, и в частности, выражениями, описывающими функционирование замкнутых систем массового обслуживание. Необходимые для проведения указанных вычислений исходные данные - N1, Л/ Ц- СППР получает либо из соответствующих баз данных, либо экспертным путем (их задает руководитель или эксперт) с помощью таблиц аналогичных таблицам 4.2 - 4.4, которые описывают, например, характеристики ремонтов скважин (их вид и частоту), имеющиеся запасы нефти, газа, подземное и наземное оборудование, число и вид бригад по проведению ремонтов, геофизических исследований скважин и др. [c.421]
Смотреть страницы где упоминается термин Переход к стационарным вероятностям
: [c.50]Смотреть главы в:
Теория очередей и управление запасами -> Переход к стационарным вероятностям
