С учетом выполнения условия (3.1) производственную функцию Кобба — Дугласа можно записать в виде [c.60]
Отсюда видно, что изокванты имеют асимптотами оси координат. Предельная норма замещения -у для производственной функции Кобба — Дугласа подсчитывается следующим образом [c.60]
Построим теперь для производственной функции Кобба — Дугласа соответствующую ей зависимость удельного выпуска от фондовооруженности / (k). Она в данном случае имеет вид [c.61]
Отметим, что, кроме свойств (2.7) — (2.9), производственная функция Кобба — Дугласа имеет следующее свойство [c.62]
В связи с этим возникает вопрос не будет ли производственная функция с постоянной эластичностью замещения при р -> 0 стремиться к производственной функции Кобба— Дугласа Оказывается, что это действительно так. Покажем, [c.66]
Блок производства содержит шесть эконометрических (статистических) соотношений (функций) и четыре тождества. Выпуск продукции в стоимостном выражении Q (/) задается производственной функцией Кобба — Дугласа от трех факторов производства (среднесписочной численности промышленно-производственного персонала L (t), среднегодового объема основных производственных фондов /С (0, суммарных материальных затрат V (t)) и автономного технического прогресса [c.109]
Нами рассчитаны двенадцать уравнений множественной линейной корреляции, четыре функции в виде полинома, пять-производственных функций Кобба — Дугласа и четырнадцать кинетических производственных функций. Для определения степени влияния отобранных факторов на результативный признак нами вычислены [c.5]
Развитие теории производственной функции связывается с производственной функцией Кобба — Дугласа. Эти авторы (США) проанализировали статистические данные американской промышленности за период 1899—1922 гг. и обосновали использование в экономическом анализе мультипликативной функции, носящей теперь их имя. [c.79]
Математический анализ производственной функции Кобба — Дугласа показывает, что при ж,- > 0 она является математически определенной, непрерывной, монотонной, выпуклой вверх ( 3г > 0) [c.80]
Линейная, параболическая и производственная функции Кобба— Дугласа не отвечают им в полной мере. Наиболее адекватной является трансцендентная функция 1 [c.84]
| Таблица 3 Мультипликативная производственная функция Кобба — Дугласа | 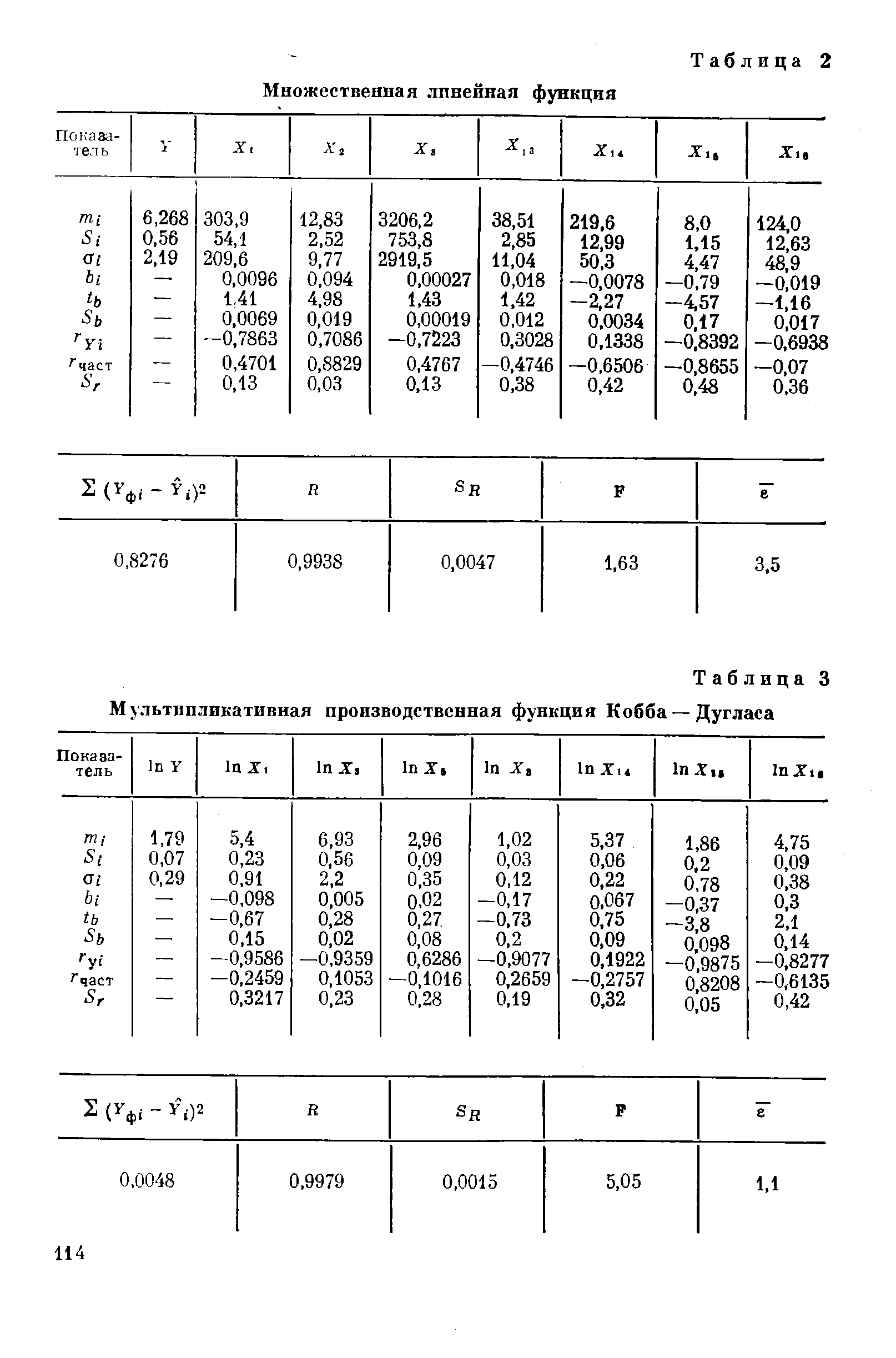 |
Каждое предприятие стремится выбрать такой технически эффективный процесс, который обеспечивал бы наименьшие издержки производства. В решении этой задачи используется производственная функция Кобба — Дугласа, которая задает выпуск продукции (У) как функцию (/) затрат капитала (К) и труда (I) [c.315]
Пример 5.4. По данным п = 50 предприятий легкой промышленности оценить производственную функцию Кобба— Дугласа в виде (5.18). [c.127]
При желании можно подвести теоретическую базу под расчет доли труда в дополнительной чистой прибыли (допустим, через производственную функцию Кобба-Дугласа), однако, действительность проще и жестче. Как правило, процент формирования премиального фонда за счет дополнительной прибыли основывается на остаточном принципе сначала предприятие смотрит на проблемы в сфере финансовой устойчивости, то есть основным приоритетом распределения гипотетической дополнительной прибыли чаше всего является пополнение собственных оборотных средств, затем — на свои инвестиционные потребности, в третью очередь (возможно) — на запросы акционеров в части дивидендов и, в последнюю очередь — на работающий персонал. Поэтому в реальных российских условиях формализация процедуры расчета процента премиального фонда в возможной дополнительной чистой прибыли только вредна. В дальнейшем будем считать, что процент формирования премиального фонда определяется высшим руководством предприятия произвольно, исходя из ситуации на начало периода. [c.513]
Первый вариант производственной функции разработал в США экономист П. Дуглас совместно с математиком Ч. Коббом в 1928 г. Формула производственной функции Кобба—Дугласа показала количественную зависимость объема выпуска продукции на предприятии от двух факторов — капитала (средств производства) и труда. В дальнейшем в этой функции было учтено влияние технического прогресса на объем изготавливаемых деталей. В итоге функция Кобба—Дугласа приняла следующий обобщенный вид [c.256]
Производственная функция Кобба—Дугласа имеет постоянную эластичность замещения производственных факторов, равную единице. Это означает, что, скажем, расширение численности рабочих (соответственно рост фонда заработной платы) эквивалентно увеличению размера капитала, которое вызовет точно такой же рост объема производства. Поэтому предпринимателю безразлично, за счет роста каких факторов наращивать выпуск продукции. Одна и та же денежная единица дает одинаковый производственный эффект независимо от того, на увеличение какого фактора она была израсходована. [c.256]
Иначе обстоит дело с криволинейной регрессией, нелинейной по оцениваемым параметрам. Предположим, что рассматривается производственная функция Кобба-Дугласа [c.117]
На рис. 8.1 даны эскизы изоквант функции Кобба- Дугласа (обычная форма производственной функции, используемая в моделировании производства на макроуровне). Производственная функция Кобба-Дугласа — это степенная функция затрат капитала и труда [c.176]
Производственная функция Кобба— Дугласа имеет постоянную эластичность замещения производственных факторов, рав- [c.173]
Общий результат трудовой деятельности — объем созданной продукции — является зависимым от функционирования основных секторов производства, их количественного и качественного уровня. Эта связь выражается производственной функцией/Экономист П. Дуглас совместно с математиком Ч. Коббом (США) разработали формулу производственной функции, имеющей следующий обобщенный вид [c.121]
Значительный вклад в развитие теории экономического роста внес Р. Солоу. Им были разработаны две модели модель факторного анализа источников экономического роста и модель, раскрывающая взаимосвязь сбережений, накопления капитала и экономического роста Основой первой модели явилась производственная функция Кобба—Дугласа. Она была модифицирована путем ввода еще одного фактора — уровня развития технологий [c.405]
Производственная функция Кобба-Дугласа имеет вид [c.250]
Параметры производственной функции Кобба-Дугласа определяются [c.250]
Параметры производственной функции Кобба-Дугласа, а точнее — коэффициенты регрессии а1 и а2 лежат в интервале [c.251]
Средняя производительность труда на основании производственной функции Кобба-Дугласа (у — общественный продукт, х1 — затраты труда и х2 — объем производственных фондов) определяется как [c.251]
В производственной функции Кобба-Дугласа предельная производительность труда [c.252]
Пусть время t изменяется дискретно (t = 0, 1,. . . ), v(i] — годовой валовой выпуск, Ф( ) — основные производственные фонды. Будем считать, что связь между v и Ф описывается производственной функцией Кобба- Дугласа и имеет вид [c.18]
Впервые производственная функция была рассчитана в 1920-х гг. американскими учёными — экономистом П. Дугласом и математиком Ч. Коббом для обрабатывающей промышленности США. Производственная функция Кобба — Дугласа имела вид Q = А х Ка х IA Предполагалось, что объём производства Q определяется фактором К (количество капитала, т. е. используемые средства производства) и фактором L (количество труда). Степенные показатели а и б отражали увеличение в процентах выпуска продукции, если количество труда или капитала увеличится на 1%. Величина А учитывала все качественные изменения факторов производства (кроме труда и капитала). [c.236]
Вывод Для производственной функции Кобба-Дугласа предельная норма JKL замещения прямо пропорциональна фондовооруженности труда К/ L, а предельная норма замещения -JLK пропорциональна трудоемкости L/K. [c.347]
Выбор производственной функции Кобба — Дугласа или функции с постоянной эластичностью замещения факторов (С 5-функции) в качестве модели для анализа и прогноза народнохозяйственной динамики представляет собой первый из охарактеризованных путей. Однако постулируемые для этих производственных функций свойства, такие, как постоянство эластичностей факторов или эластичности их замещения, могут, не реализуясь в фактическом процессе взаимодействия факторов, приводить к чрезмерно усредненному или неадекватному описанию экономического [c.31]
Впервые подобная функция рассматривалась, по-видимому, американским специалистом А. Хальтером и его коллегами. Она приводится в монографии Э. Хеди и Д. Диллона [103]. Широкое использование нашла эта функция в работах Б. И. Искакова [49], который дал этой функции название кинетическая . Эта функция привлекает внимание исследователей своими специфическими особенностями. Она сложнее производственной функции Кобба — Дугласа, но обладает по сравнению с нею более гибкими свойствами. Смена знака у параметра уг с положительного на отрицательный преображает вид этой функции и придает ей новое содержание. [c.80]
В качестве примера использования линеаризирующего преобразования регрессии рассмотрим производственную функцию Кобба—Дугласа [c.126]
Производственная функция Кобба—Дугласа — функция, определяющая взаимозаменяемость труда и капитала. Выведена в 20-х гг. американскими учеными К. Коббоми П.Дугласом [c.886]
