Позже влияние НТП было обозначено отдельным фактором в производственной функции Кобба-Дугласа [c.13]
С учетом выполнения условия (3.1) производственную функцию Кобба — Дугласа можно записать в виде [c.60]
Отсюда видно, что изокванты имеют асимптотами оси координат. Предельная норма замещения -у для производственной функции Кобба — Дугласа подсчитывается следующим образом [c.60]
Отсюда видно, что предельная норма замещения для функции Кобба — Дугласа является линейной функцией фондовооруженности K/L и при пропорциональном росте факторов производства не изменяется. Подсчитаем эластичность замещения а. Предварительно заметим, что на изокванте фондовооруженность как функция предельной нормы [c.60]
Таким образом, для рассматриваемой здесь производственной функции (3.2) коэффициенты эластичности выпуска по ресурсам производства постоянны и равны показателям степеней при величинах ресурсов. Поэтому, вспоминая экономический смысл коэффициентов Ек и EL, можно сказать, что экономический смысл показателей степеней функции Кобба — Дугласа состоит в том, что они являются отношениями предельных эффективностей использования соответствующих ресурсов к средним эффективностям. [c.61]
Построим теперь для производственной функции Кобба — Дугласа соответствующую ей зависимость удельного выпуска от фондовооруженности / (k). Она в данном случае имеет вид [c.61]
Отметим, что, кроме свойств (2.7) — (2.9), производственная функция Кобба — Дугласа имеет следующее свойство [c.62]
Другим недостатком функции Кобба — Дугласа является равенство единице эластичности замещения ресурсов. Часто экономические соображения подсказывают, что, хотя эластичность замещения ресурсов и можно считать постоянной, равенство ее единице вряд ли верно. В связи с этим вызывает интерес вопрос о возможности построения производственной функции с постоянной положительной эластичностью замещения о. Такая функция была пред- [c.62]
Эта кривая имеет две асимптоты. При L - + °° основные фонды К постоянно убывают, но стремятся не к нулю, как в случае функции Кобба — Дугласа, а к некоторому положительному числу [c.64]
Легко заметить, что здесь, как и в случае функции Кобба— Дугласа, Ек < 1, EL < 1, т. е. предельная эффективность ресурса меньше средней. Заметим, что коэффициенты эластичности ресурсов можно записать также в другом виде, эквивалентном уже полученному [c.65]
Обратим внимание читателя на то, что при стремлении величины р к нулю все характеристики функции ES стремятся к соответствующим характеристикам функции Кобба — Дугласа. Действительно, [c.66]
В связи с этим возникает вопрос не будет ли производственная функция с постоянной эластичностью замещения при р -> 0 стремиться к производственной функции Кобба— Дугласа Оказывается, что это действительно так. Покажем, [c.66]
Поскольку функция / (и) однозначно определяет F (К, L), мы доказали утверждение о том, что функция Кобба — Дугласа получается из функции ES путем предельного перехода при р -> 0. [c.67]
На этом мы заканчиваем рассмотрение производственных функций с двумя факторами. В заключение скажем, какие же производственные функции лучше выбирать для описания народного хозяйства. Функция с постоянными пропорциями вряд ли подходит для этого, поскольку увеличение одного из производственных ресурсов обычно приводит к некоторому увеличению объема производства. Ее применяют лишь тогда, когда один из ресурсов производства резко дефицитен, а второй избыточен. Таким образом, остаются степенные функции (в том числе функция Кобба — Дугласа) и функции с постоянной эластичностью замены. Надо сказать, что степенные функции используются чаще, поскольку параметры степенных производственных функций оценить значительно легче и работать со степенными функциями проще. Их основной недостаток — возможность полной замены одного ресурса другим — часто не является существенным, поскольку в исследованиях бывают интересны значения ресурсов, достаточно близкие к уже использующимся в производстве в данный момент. Поэтому неправдоподобность поведения степенных функций в области малых количеств ресурсов не так уж важна. [c.71]
При достаточно большой эластичности замены (т. е. при достаточно малых значениях р) величина / (0) велика, а для функции Кобба — Дугласа даже бесконечно велика. Поэтому для производственной функции с достаточно большой эластичностью замены условие (4.14) при малых k > 0 выполняться не может, тем более, что параметр г имеет величину порядка нескольких процентов. [c.75]
Для функции Кобба — Дугласа также можно показать, что ф (k) < 0 при достаточно больших значениях k. Хотя функция Кобба — Дугласа и не имеет асимптоты при k - оо, при достаточно больших справедливо соотношение [c.76]
Функция Кобба — Дугласа. Функция Кобба — Дугласа имеет следующий вид [c.100]
Из выражения (2.3) мы видим, что если производство описывается функцией Кобба — Дугласа, то темп роста производства у/у линейно зависит от темпов роста затрат факторов х /х (t = 1,. .., ) [c.101]
Линии равного выпуска функции Кобба — Дугласа для случая двух ресурсов изображены на рис. 6, а график зависимости производительности труда от фондовооруженности — на рис. 5. [c.101]
Отсюда замечаем, что при р - —1 имеем % -> оо (линейная функция с бесконечной эластичностью), при р - 0 получаем Оу - 1 (функция Кобба — Дугласа с эластичностью замещения, равной единице). Наконец, при р -> оо получаем ац -> 0 (функция с фиксированными пропорциями затрат). [c.103]
Блок производства содержит шесть эконометрических (статистических) соотношений (функций) и четыре тождества. Выпуск продукции в стоимостном выражении Q (/) задается производственной функцией Кобба — Дугласа от трех факторов производства (среднесписочной численности промышленно-производственного персонала L (t), среднегодового объема основных производственных фондов /С (0, суммарных материальных затрат V (t)) и автономного технического прогресса [c.109]
Производственная функция (ПФ), описывающая случай, когда (ос + (3) = 1, называется функцией Кобба-Дугласа и должна быть рассмотрена подробно по курсу Макроэкономика . [c.140]
Функции Кобба-Дугласа 97 Функция 51, 55 [c.478]
Нами рассчитаны двенадцать уравнений множественной линейной корреляции, четыре функции в виде полинома, пять-производственных функций Кобба — Дугласа и четырнадцать кинетических производственных функций. Для определения степени влияния отобранных факторов на результативный признак нами вычислены [c.5]
Наиболее часто рекомендуется пользоваться следующими функциями прямая зависимость, полином с целочисленными степенями, степенная функция, показательная функция. В настоящей работе рассматриваются гипотезы о наличии связи между себестоимостью добычи нефти и попутного газа и факторами в форме множественной линейной, полиномов трех первых степеней, мультипликативная функция Кобба — Дугласа и кинетическая производственная функция. [c.79]
Развитие теории производственной функции связывается с производственной функцией Кобба — Дугласа. Эти авторы (США) проанализировали статистические данные американской промышленности за период 1899—1922 гг. и обосновали использование в экономическом анализе мультипликативной функции, носящей теперь их имя. [c.79]
Математический анализ производственной функции Кобба — Дугласа показывает, что при ж,- > 0 она является математически определенной, непрерывной, монотонной, выпуклой вверх ( 3г > 0) [c.80]
Мультипликативная функция Кобба — Дугласа [c.84]
Линейная, параболическая и производственная функции Кобба— Дугласа не отвечают им в полной мере. Наиболее адекватной является трансцендентная функция 1 [c.84]
Корреляционная модель себестоимости добычи нефти и попутного газа по указанным факторам была рассчитана по мультипликативной функции Кобба — Дугласа (41). В результате решения этой модели было составлено сводное уравнение по нефтедобывающей промышленности Украинской ССР [c.90]
Коэффициенты этой регрессии являются параметрами функции Кобба — Дугласа [c.90]
| Таблица 3 Мультипликативная производственная функция Кобба — Дугласа | 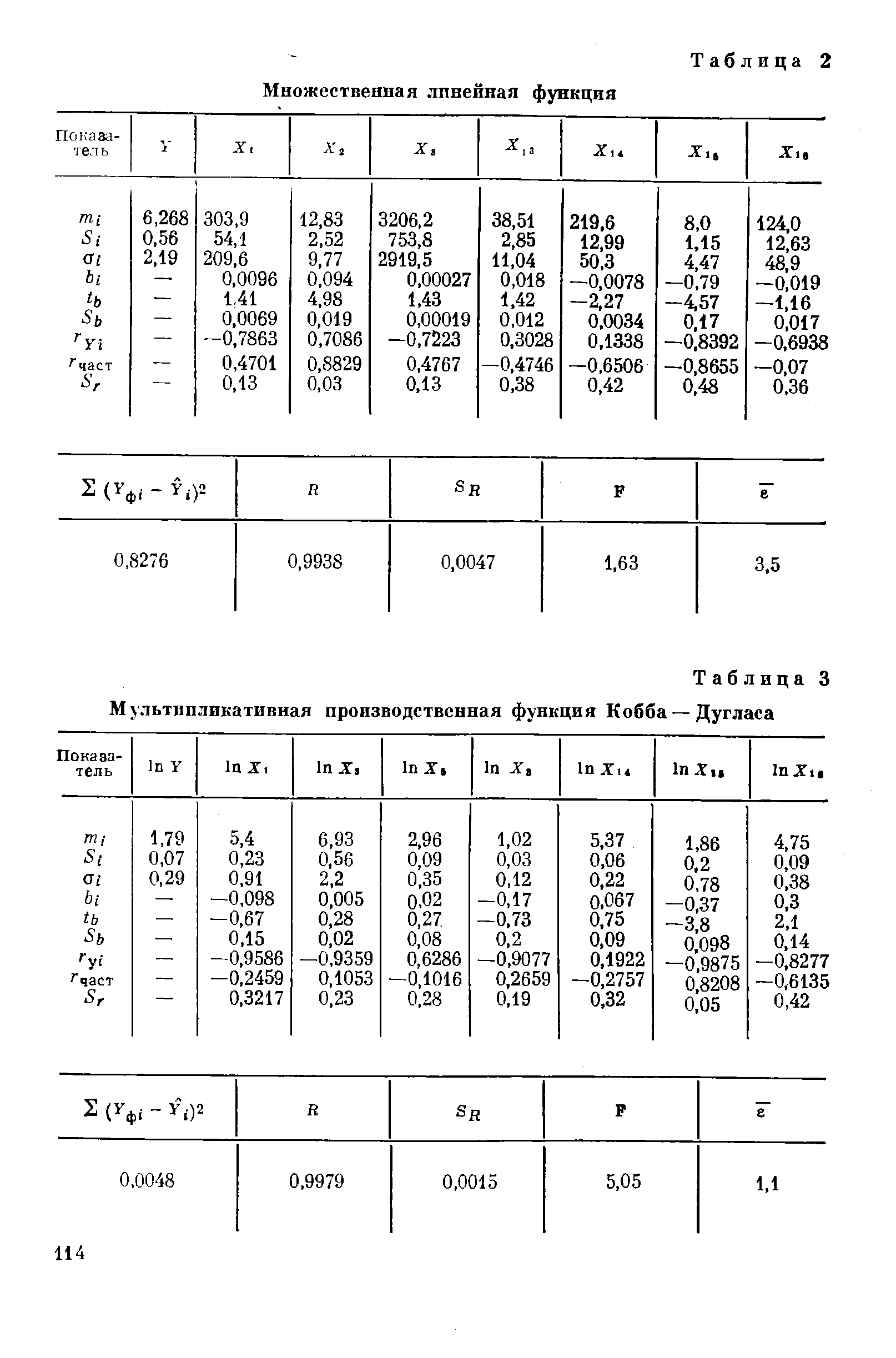 |
На практике для определения объемов производства при различной комбинации факторов используют производственную функцию Кобба — Дугласа (названную по именам ученых-американцев, которые ее предложили) [c.149]
Проведем предельные переходы. Применяя при р -> О правило Лопиталя к функции (2.10), получаем логарифмическую формулу функции Кобба — Дугласа [c.103]
Заменяя pYynaa/ и потенцируя, получаем функцию Кобба — Дугласа в обычной форме [c.104]
В 1928 году американские ученые — математик Ч. Кобб и экономист П. Дуглас проанализировали статистические данные по обрабатывающей промышленности США и обнаружили связь между количеством отработанных человеко-часов (L) и величиной основного капитала (К), с одной стороны, и величиной национального дохода (У) — с другой. На основании исследований они вывели зависимость, которая вошла в историю под названием функции Кобба —Дугласа (двухфак-торная модель). В данной модели учитывалось два фактора капитал и труд. Она может быть представлена в следующем виде [c.97]
Впервые подобная функция рассматривалась, по-видимому, американским специалистом А. Хальтером и его коллегами. Она приводится в монографии Э. Хеди и Д. Диллона [103]. Широкое использование нашла эта функция в работах Б. И. Искакова [49], который дал этой функции название кинетическая . Эта функция привлекает внимание исследователей своими специфическими особенностями. Она сложнее производственной функции Кобба — Дугласа, но обладает по сравнению с нею более гибкими свойствами. Смена знака у параметра уг с положительного на отрицательный преображает вид этой функции и придает ей новое содержание. [c.80]
При построении моделей себестоимости добычи нефти и газа по НГДУ Прикарпатья (линейная, полином третьей степени мультипликативная функция Кобба — Дугласа) ни одна из них не выдержала проверки на адекватность (табл. 29). Величины критериев, характеризующих экономико-статистическую достоверность кинетической производственной функции по нефтегазодобывающим управлениям Прикарпатья, приведены в табл. 30. [c.94]
Построенные многофакторные корреляционные модели по нефте-х добывающей промышленности Украины, нефтегазодобывающим управлениям Прикарпатья, НГДУ Долинанефтегаз вида множественной линейной функции, мультипликативной функции Кобба — Дугласа, кинетической производственной функции позволили сделать количественную оценку влияния различных факторов в их взаимосвязи на динамику себестоимости добычи нефти и попутного газа. Исследована специфика экономико-математического моделирования в нефтедобывающей промышленности, и с этих позиций обосновано использование в качестве функции себестоимости добычи нефти и газа кинетической трансцендентной функции вида [c.111]
