| Рис. 3.2 Будущая стоимость аннуитета. |  |
При какой ставке годовых процентов будущая стоимость аннуитета из 10 периодов в 2 раза больше, чем арифметическая сумма платежей (величина платежа, умноженная на 10). [c.315]
В предыдущем параграфе мы рассмотрели понятие аннуитета, рассчитали значение будущей стоимости различных аннуитетов. Однако часто перед нами встает задача противоположная нахождению будущей стоимости аннуитета. [c.316]
Допустим, нам известна величина будущей стоимости (предположим, что мы хотим накопить на банковском депозите определенную сумму денег, например, 10 000 долларов на покупку автомобиля). В этом случае нам надо найти величину платежа, которая обеспечит накопление требуемой суммы по истечении п платежных периодов. Из формулы будущей стоимости аннуитета мы делаем вывод, что величина каждого платежа (РМТ) в слу- [c.316]
| Рис. 3.14 Расчет значений второй функции — будущей стоимости аннуитета | 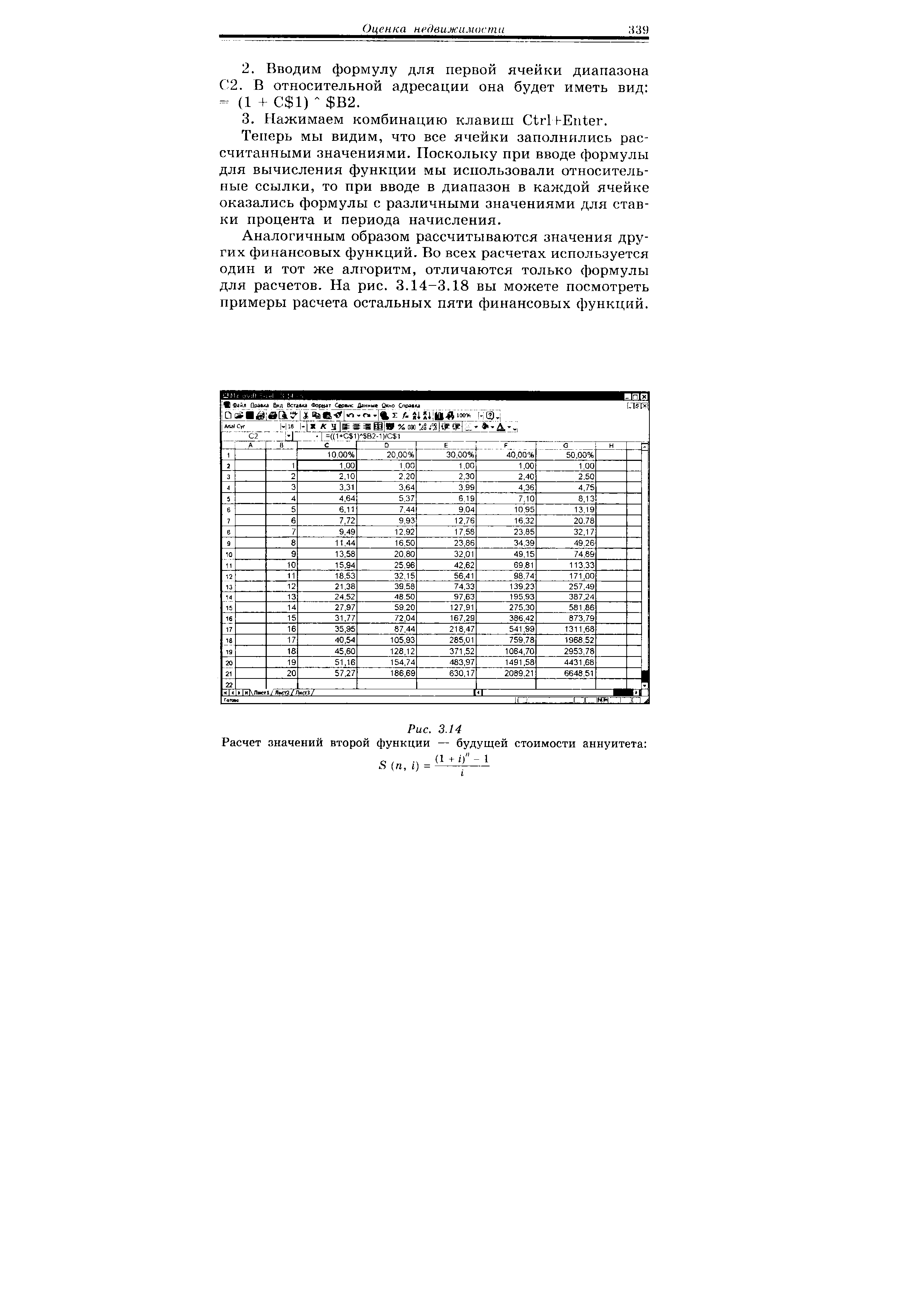 |
Для определения будущей стоимости аннуитета можно воспользоваться формулой (116). Для наглядности представим результаты расчетов в табличном виде. [c.297]
Из таблицы видно, что на первое денежное поступление в размере 20 тыс. руб. начисляются сложные проценты за 4 года и оно в конце пятого года станет равным 20 2,4414 = 48,828 тыс. руб. на второе денежное поступление в размере 12 тыс. руб. начисляются сложные проценты за 3 года и оно в конце пятого года станет равным 12 1,9531 = 23,4372 тыс. руб. и т.д. Будущая стоимость аннуитета равна сумме наращенных поступлений, т.е. FV a =171,0152 тыс. руб. [c.297]
Имеется переменный аннуитет постнумерандо (тыс. руб.) 14, 40, 25, 10. Рассчитайте а) будущую стоимость аннуитета б) приведенную стоимость аннуитета, если его период совпадает с базовым периодом начисления процентов по сложной процентной ставке 30% годовых, т.е. равен одному году. Как изменятся полученные оценки, если исходный поток представляет собой аннуитет пренумерандо [c.305]
Пример 3.3.3. На счет в банке в начале каждого двухлетнего периода будет поступать по 8 тыс. руб. в течение 10 лет. Требуется определить а) будущую стоимость аннуитета б) приведенную стоимость аннуитета, если на поступающие суммы будут ежегодно начисляться декурсивные сложные проценты по ставке 22% годовых. [c.309]
Оценка непрерывного аннуитета а) будущая стоимость аннуитета [c.338]
Оценка переменного аннуитета постнумерандо, платежи которого образуют арифметическую прогрессию а) будущая стоимость аннуитета [c.339]
| Таблица 2 Будущая стоимость аннуитета платежей в IS |  |
Пример Необходимо рассчитать будущую стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо), при следующих данных период платежей по аннуитету предусмотрен в количестве 5 лет [c.135]
Подставляя эти значения в приведенную формулу, получим будущая стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо), равна [c.135]
При расчете будущей стоимости аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), применяется следующая формула [c.135]
Пример Необходимо рассчитать будущую стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), по данным, изложенным в предыдущем примере (при условии взноса платежей в конце года). [c.135]
Сопоставление результатов расчета по двум примерам показывает, что будущая стоимость аннуитета, осуществляемого на условиях предварительных платежей, существенно превышает будущую стоимость аннуитета, осуществляемого на условиях последующих платежей, т.е. в первом случае инвестору обеспечена гораздо большая сумма дохода. [c.136]
При расчете размера отдельного платежа при заданной будущей стоимости аннуитета используется следующая формула [c.137]
В этом случае формула для определения будущей стоимости аннуитета (осуществляемого на условиях последующих платежей), имеет вид [c.138]
Будущая стоимость аннуитета [c.88]
При расчете будущей стоимости аннуитета, несомненно, имеет значение вид аннуитета — немедленный, как в нашем примере, или обычный. В случае с обычным аннуитетом первый взнос в размере 100 долл. делается в конце первого периода. Рис. 4.6 показывает временной график, где рассматриваются обе ситуации. Хотя и в том, и в другом случае количество платежей одинаково, при немедленном аннуитете на общую сумму начисляются проценты за дополнительный год. Таким образом, FV немедленного аннуитета равнялась бы FV обычного аннуитета, умноженного на 1 + /. Для обычного аннуитета величиной 1 доля, в год формула для вычисления будущей стоимости выглядит следующим образом [c.88]
Существует три основных метода вычисления коэффициента наращения будущей стоимости аннуитета [c.28]
Коэффициенты будущей стоимости аннуитета для различных периодов времени п и процентных ставок г можно найти в Таблицах наращения и дисконтирования. [c.28]
Как определяется настоящая и будущая стоимость аннуитета [c.32]
| Рис. 5. Будущая стоимость аннуитета постнумерандо | 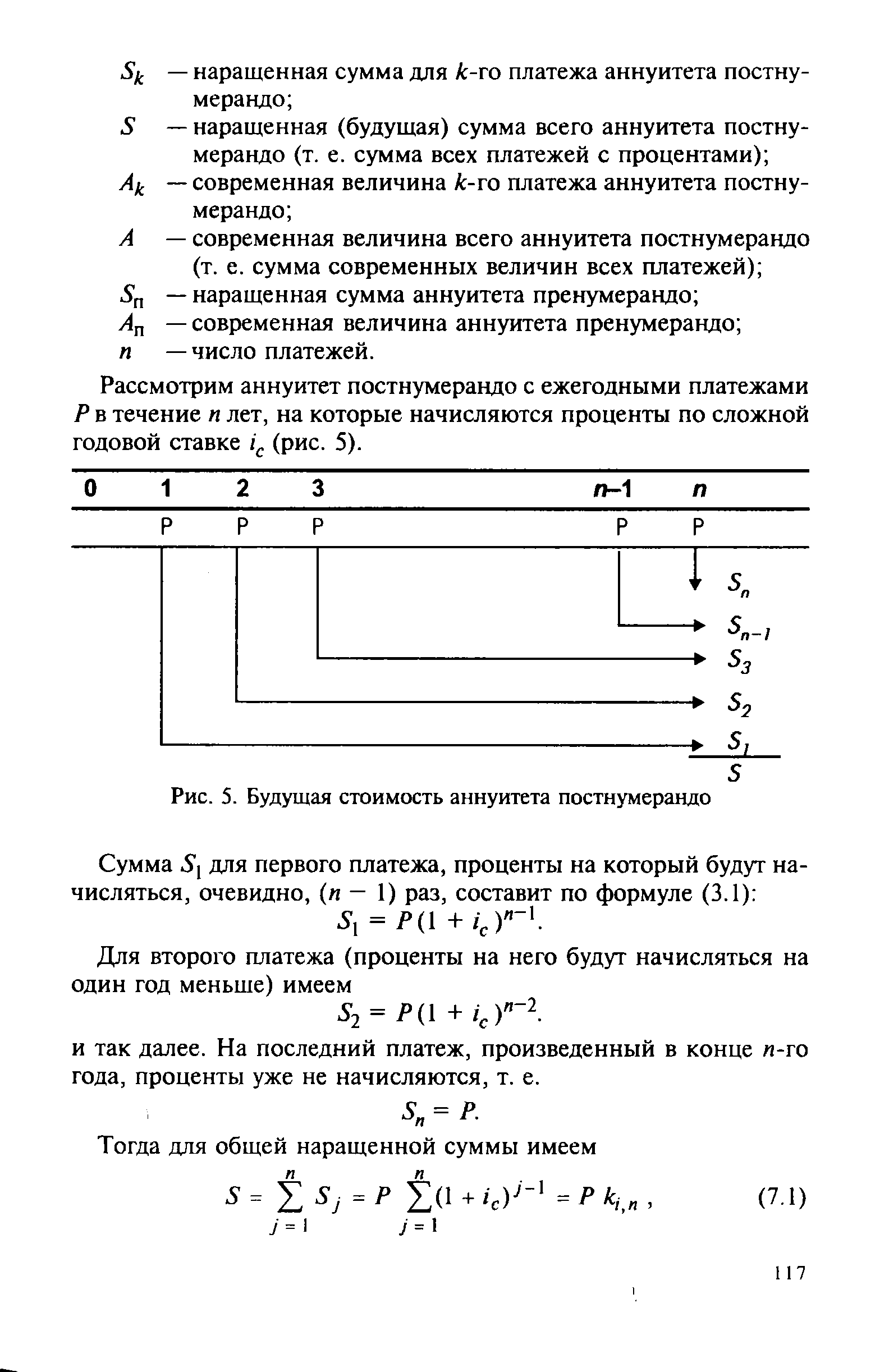 |
| Рис. 7. Будущая стоимость аннуитета пренумерандо |  |
