Базовые понятия простой и сложный процент номинальная и реальная ставка процента настоящая и будущая стоимость доходность к аукциону и доходность к погашению. [c.377]
Когда происходит сравнение альтернативных проектов, то денежные потоки приводятся к начальному году и это приведение осуществляется по формуле вложенных процентов. А сам процесс называется дисконтированием, т.е. определяет настоящую стоимость через будущую стоимость. [c.95]
Отсюда формула для исчисления будущей стоимости денег (для сложных процентов) такова [c.449]
Очевидно, что 1289 — это будущая стоимость 1000 ф.ст., инвестированных на три года под 8 % годовых с капитализацией процента, т. е. приведенная стоимость 1289 ф.ст. при 8 % годовых равна 1000 ф.ст. Приведение будущих сумм к сегодняшнему их [c.449]
Итак, 572 тыс. руб. — это рассчитанная будущая стоимость, отражающая реальную цену первоначально вложенных средств (200 тыс. руб.) после прохождения ими четырех оборотов при банковской ставке 120% годовых. [c.276]
Kt — будущая стоимость капитала к концу года t, руб. [c.277]
Исходя из этого принципа следует не только знать стандарты соответствия для данного рынка недвижимости, но и следить за тенденциями их развития, чтобы предвидеть будущую стоимость оцениваемого объекта недвижимости. [c.250]
Следует не забывать, что понятия текущей и будущей стоимости являются относительными понятиями. Они применимы только в том случае, если мы выбрали точку отсчета во времени, относительно которой мы вычисляем значения текущей и будущей стоимости. К примеру, текущая стоимость 2000 долларов, которые будут получены 1 января 2000 года будет иметь различные значения на 1 января 1998 года или на 1 июля 1997 года. Аналогичный пример можно привести и для будущей стоимости. Если быть точнее, то текущая и [c.305]
В дальнейшем мы будем рассматривать оценку денежных сумм, для которых существует возможность альтернативного вклада в банк с получением процентов. Поэтому для оценки текущей стоимости таких денег необходимо в расчет вводить соответствующие поправки. Процессы преобразования между текущей и будущей стоимостью аккумулированием и дисконтированием. [c.306]
Аккумулирование — это процесс приведения текущей стоимости денег к их будущей стоимости при условии, что эта сумма удерживается на счету в течение определенного времени, принося периодически накапливаемый процент. [c.306]
Первая функция денег — будущая стоимость денежной единицы (накопленная сумма единицы). [c.309]
Утверждение. Будущая стоимость суммы денег может быть рассчитана по формуле [c.309]
| Рис. 3.1 Будущая стоимость денежной единицы |  |
Именно в виде 3.7 функция будущей стоимости денежной единицы определяется как классическая финансовая функция. На рисунке (3.1) изображены графики первой финансовой функции при различных значениях ставки процента г. [c.310]
Приведенные выше расчеты основывались на том предположении, что начисление процентов происходит один раз в год. Теперь мы собираемся расширить применение формулы будущей стоимости для того случая, когда аккумулирование происходит несколько раз в год, например, в случае, если платежный период равен 1 месяц, 1 квартал, 1 полугодие. [c.310]
Будущая стоимость капитала при периоде начисления меньшем, чем один год, имеет вид [c.311]
Банк применяет процентную политику, в соответствии с которой на сумму депозита начисляются как сложные, так и простые проценты. Сложные проценты начисляются на полную сумму денег, находящуюся на счету на момент начисления, простые проценты начисляются на сумму, первоначально положенную на депозит. Напишите возможный вариант формулы вычисления будущей стоимости денег на таком депозите. [c.312]
Вторая финансовая функция — будущая стоимость аннуитета. [c.313]
Теперь попробуем вычислить будущую стоимость п-периодного аннуитета. Сначала рассмотрим обычный аннуитет. [c.313]
Очевидно, что будущая стоимость по окончании первого платежного периода (FV ) будет равна [c.313]
В данном случае мы имеем дело с геометрической прогрессией, поэтому применив известную из курса математики формулу суммы членов геометрической прогрессии, мы получаем выражение для будущей стоимости обычного n-периодного аннуитета [c.314]
| Рис. 3.2 Будущая стоимость аннуитета. |  |
| Рис. 3.3 Будущая стоимость авансового аннуитета. |  |
Допустим, нам известна величина будущей стоимости (предположим, что мы хотим накопить на банковском депозите определенную сумму денег, например, 10 000 долларов на покупку автомобиля). В этом случае нам надо найти величину платежа, которая обеспечит накопление требуемой суммы по истечении п платежных периодов. Из формулы будущей стоимости аннуитета мы делаем вывод, что величина каждого платежа (РМТ) в слу- [c.316]
Величину текущей стоимости нетрудно найти из формулы будущей стоимости капитала [c.319]
Часто бывает так, что требуется оценить текущую стоимость серии платежей, т. е. аннуитета. Как и в случае будущей стоимости, мы будем рассматривать обычный и авансовый аннуитеты. [c.321]
Рассмотрим конкретную задачу требуется рассчитать значения финансовой функции (например, первой функции — будущей стоимости единицы) для значений ставки процента 10%, 20%, 30%, 40%, 50% для количества периодов до 20 включительно. Очевидно, что решение этой задачи сводится к стократному (пять значений процента умножаются на 20 периодов начисления) применению известной нам формулы [c.337]
| Рис. 3.13 Расчет значений таблицы будущей стоимости единицы FV — (1+ i)" |  |
| Рис. 3.14 Расчет значений второй функции — будущей стоимости аннуитета | 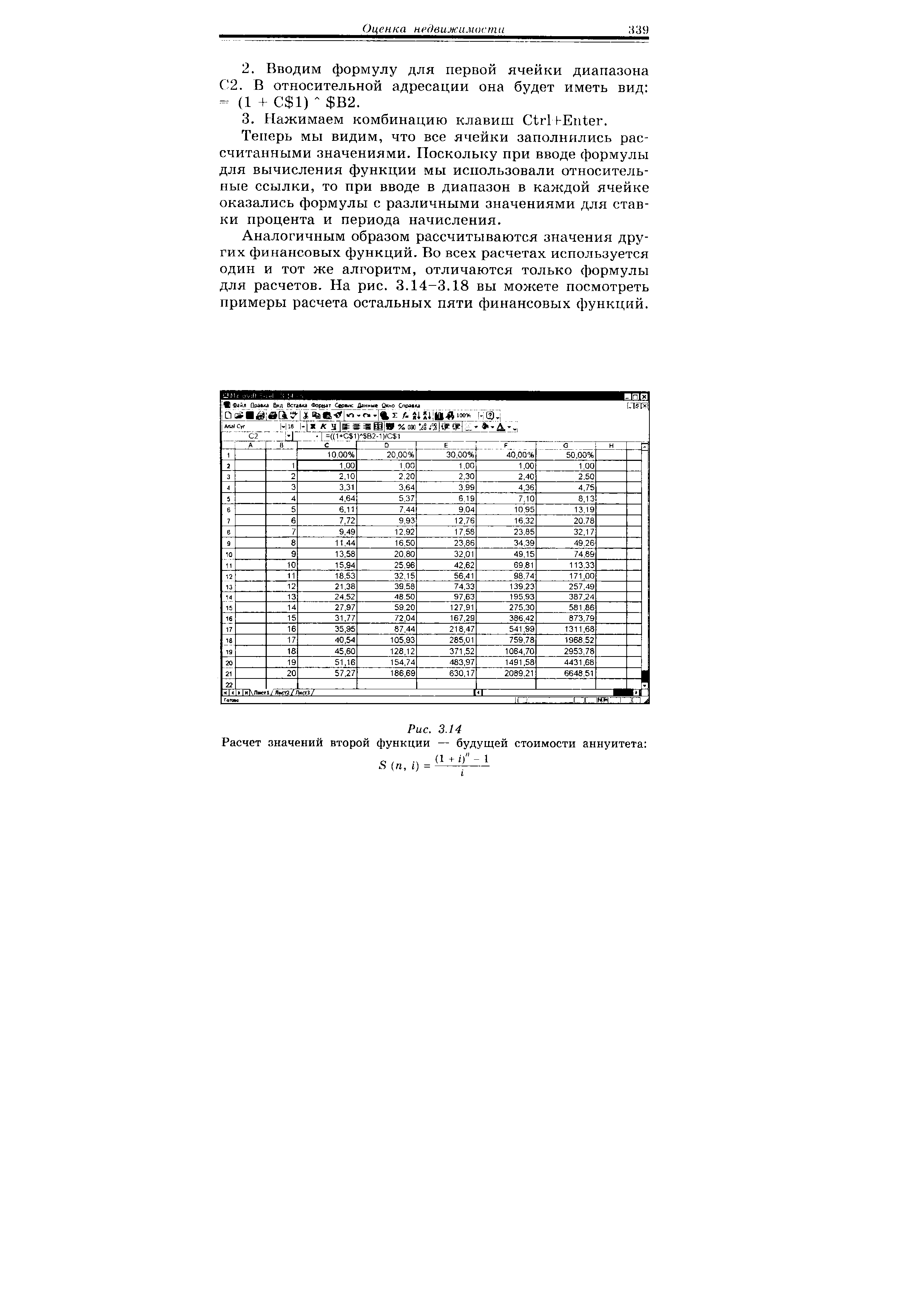 |
Смотреть страницы где упоминается термин Будущая стоимость
: [c.95] [c.449] [c.450] [c.450] [c.450] [c.276] [c.305] [c.306] [c.308] [c.308] [c.309] [c.313] [c.317] [c.396] [c.396] [c.420]Основы инвестирования (0) -- [ c.0 , c.214 , c.215 , c.216 , c.691 ]
Дисциплинированный трейдер (2004) -- [ c.0 ]
