Если перспектива характеризуется нарастанием нашего незнания некоторых условий предстоящего развития отраслевой системы, то чем позже делаются затраты (при прочих равных условиях), тем лучше, т. е. чем выше удельный момент затрат , тем более адаптивен план. Эту тенденцию можно усилить, если принять, что момент затрат представляет собой по-прежнему сумму произведений соответствующих порций затрат на число лет, отделяющее их от начала планируемого периода. Каждое из слагаемых суммы умножается еще и на коэффициент, в какой-то степени возрастающий с увеличением этого числа лет. Характер последней зависимости должен соответствовать характеру роста нашего незнания будущих условий реализации плана. Можно допустить, например, в порядке первого приближения, что эта зависимость описывается функцией сложных процентов (как это сделано для дисконтирования затрат по фактору времени). Тогда конструирование показателя момент затрат сведется к дисконтированию затрат по двум коэффициентам Bt и t [c.40]
В соответствии с этим коэффициент капитализации включает норму процента для получения дохода на капитал и коэффициент фонда возмещения (3-я функция сложного процента), который обеспечивает полный возврат начальных инвестиций за счет формирования фонда возмещения [c.106]
Коэффициент капитализации для зданий и сооружений можно взять из таблицы шести функций сложного процента (колонка — взнос на амортизацию денежной единицы) или можно рассчитать по формуле [c.191]
Фактор сложного процента берется из таблицы шести функций сложного процента. Например, если предполагается, что стоимость земли будет расти по индексу инфляции на 10% в год в течение следующих 8 лет, то фактор находим в колонке фактора сложного процента за 8 лет при 10%. В случае со зданиями и сооружениями из индекса инфляции (10% в год) нужно вычесть процент износа, например, 2% и получим 8% реального роста в год. Таким образом, для зданий и сооружений фактор роста найдем в той же колонке, но уже 8 лет и 8%. [c.193]
Рассмотрим подробнее шесть функций денег, шесть функций сложного процента. [c.155]
Для анализа денежных потоков от недвижимости и бизнеса, для определения текущей стоимости инвестиций, обоснования величины платы за получение будущих потоков дохода, широко применяются функции сложных процентов. Что это такое [c.96]
Функции сложного процента (20%, начисление процентов ежегодно) [c.97]
Рассмотрим перечисленные выше функции сложного процента. [c.99]
Функции сложного процента взаимосвязаны (табл. 4.3). [c.102]
| Таблица 4.3 Взаимосвязь функций сложного процента | 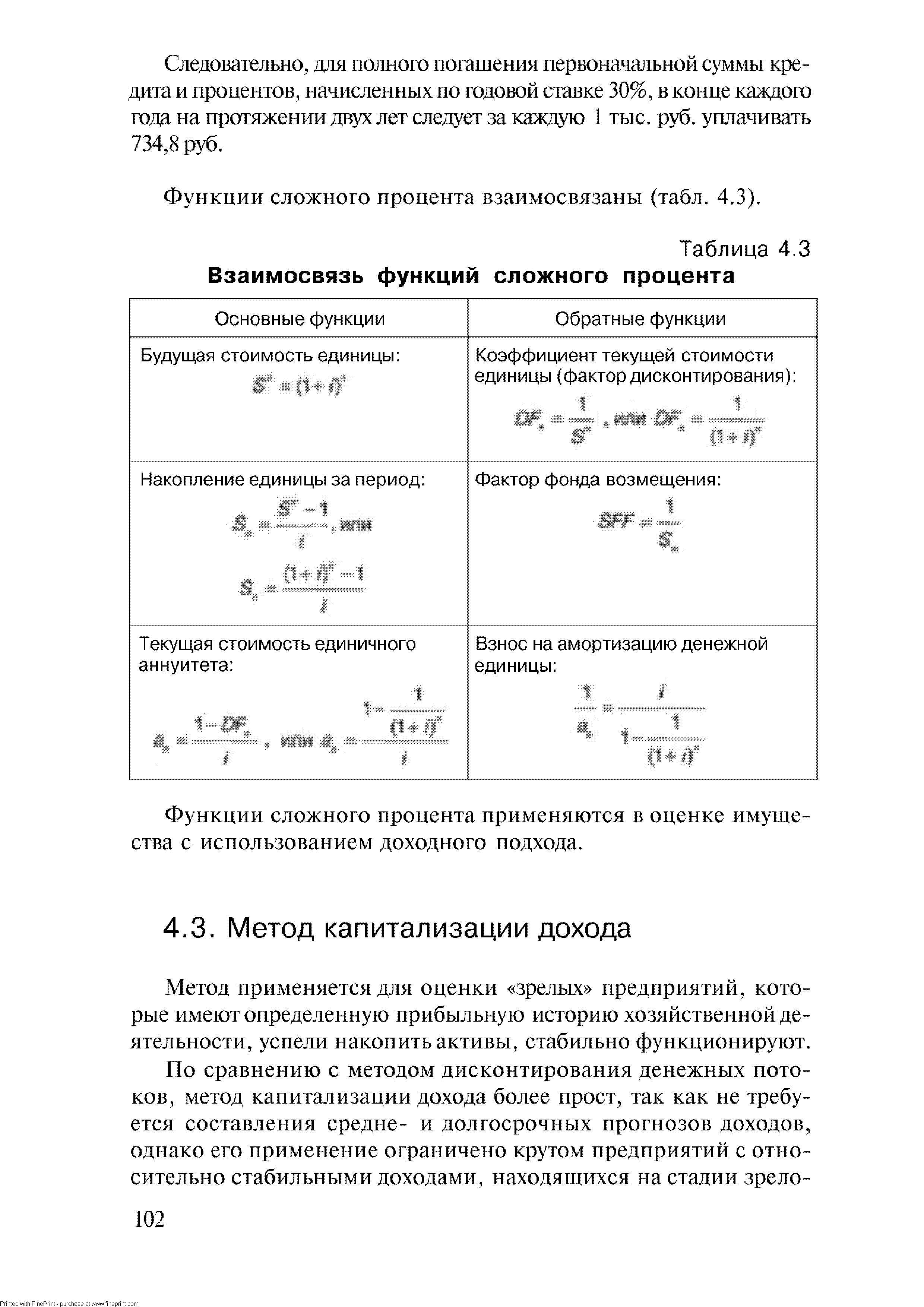 |
Для упрощения расчетов по уже приведенным и далее приводимым формулам в практических целях рекомендуется пользоваться так называемыми таблицами шести функций сложного процента. Они составлены как номографические таблицы, где численные значения всех функций сложного процента для различных ставок процента (отдельно для ежегодного начисления процента и помесячного его начисления) уже вычислены и имеют следующий вид. [c.143]
Шесть функций сложного процента [c.143]
Указанная неизвестная величина х вычисляется отталкиваясь от необходимой суммы накопления 200 ден. ед. в год номер 3 с использованием функции текущей стоимости реверсии единицы (см. таблицу шести функций сложного процента при ставке процента в 15% - функция 3). При этом текущая стоимость необходимых 200 ден. ед. определяется по состоянию на текущий момент, который соответствует году номер 1 - иначе говоря, приведение по фактору времени этих 200 ден. ед. осуществляется от года номер 3 к году номер 1, т.е. на два года [c.145]
Перечислите функции сложного процента, которые используются для пересчета денежных потоков финансово автономного бизнеса [c.154]
Численные значения ответов получены при округлении факторов соответствующих функций сложного процента до третьего знака после целой части числа величины, вычисляемые по рассмотренным в настоящей главе формулам, округляются до первого знака после целой части числа). [c.155]
Какая из ниже перечисленных функций сложного процента является обратной функции фактора фонда возмещения [c.156]
Функции сложного процента [c.148]
Связь между базовыми функциями сложного процента [c.152]
Ипотечная постоянная определяется по таблице шести функций сложного процента она равна сумме ставки процента и фактора фонда возмещения или же равна фактору взноса на единицу амортизации. [c.53]
Основной предмет финансовой математики - шесть функций денег (или шесть функций сложного процента). Перечислим эти шесть функций и их обозначения в экономических формулах [c.53]
Вторая функция сложного процента показывает, какой будет стоимость серии равных сумм, депонированных в конце каждого из периодических интервалов, по истечении установленного срока. [c.54]
Далее, воспользуемся соотношением между шестой и третьей функциями сложного процента [12] [c.166]
Приведение денежных сумм, возникающих в разное время, к сопоставимому виду называется временной оценкой денежных потоков. Временная оценка денежных потоков основана на использовании шести функций сложного процента, или шести функций денежной единицы. [c.39]
Теория и практика использования указанных функций сложного процента базируются на ряде допущений. [c.40]
Таблицы типа А систематизированы по видам функций сложного процента. Для их применения необходимо определить используемую функцию и на пересечении строки, соответствующей периоду, и столбца, адекватного ставке дисконта, найти множитель, позволяющий откорректировать ту или иную сумму. [c.40]
Функция дисконтирования является обратной по отношению к функции сложного процента. [c.45]
Назовите функции сложного процента. Какие из них находятся в обратной зависимости. [c.57]
Если условия кредита известны, то ипотечная постоянная определяется по таблицам шести функций сложного процента она представляет собой сумму ставки процента и коэффициента фонда возмещения или равна коэффициенту взноса на амортизацию единицы. [c.162]
Фактор сложного процента берется из таблицы шести функций сложного процента. Например, если предполагается, что стоимость земли растет с учетом индекса инфляции на 10% в год в течение следующих 8 лет, то фактор находим в колонке фактора сложного процента за 8 лет при 10%. В слу- [c.180]
БУДУЩАЯ СТОИМОСТЬ АННУИТЕТА (НАКОПЛЕНИЕ ДЕНЕЖНОЙ ЕДИНИЦЫ ЗА ПЕРИОД) - одна из шести функций сложного процента, позволяющая определить коэффициент для расчета будущей стоимости периодических равновеликих взносов при известных текущей стоимости взноса, процентной ставке и числе периодов. [c.496]
Метод Инвуда. Этот метод применяется, когда ожидается, что в течение всего прогнозного периода будут получены постоянные, равновеликие доходы. Одна часть этого потока доходов будет представлять собой доход на инвестиции, а другая будет обеспечивать возмещение или возврат капитала. Более того, сумма потока доходов будет представлять собой доход на инвестиции, а другая будет обеспечивать возмещение или возврат капитала. Более того, сумма возврата капитала будет реинвестироваться по ставке дохода на инвестиции (капитал). В этом случае норма возврата инвестиций как составная часть коэффициента капитализации будет равна фактору фонда возмещения при той же ставке процента, что и по инвестициям (этот фактор берется из таблицы шести функций сложного процента). Сам же коэффициент капитализации при потоке равновеликих доходов будет равен сумме ставки [c.167]
В первой ситуации, как и ранее, предполагается, что не только средства, вложенные, например, на депозит, не изымаются с него в течение п лет (кварталов, месяцев), но не изымаются и начисляемые на них проценты (что делает возможным примененить для оценки накопленнной за п периодов суммы функцию сложного процента). [c.32]
Согласно модели Инвуда в коэффициенте капитализации ограниченного во времени постоянного дохода и норма текущего дохода, и норма возврата капитала основываются на учитывающей риски бизнеса месячной ставке дисконта i = 0,06. Оценка бизнеса тогда производится по рассматривавшейся выше формуле модели Инвуда и дает такую величину рыночной стоимости бизнеса (здесь и выше могут быть использованы номограммы функций сложного процента - см. подробнее в Модуле 9 капитализация постоянного дохода по модели Инвуда тождественна функции обычного аннуитета по единице в течение 15 периодов, домноженной на Лер единиц среднемесячного ожидаемого за 15 месяцев денежного потока) [c.70]
Смотреть страницы где упоминается термин Функции сложного процента
: [c.99] [c.168] [c.155] [c.155] [c.145] [c.151] [c.153] [c.153] [c.47] [c.159]Смотреть главы в:
Методы оценки и технической экспертизы недвижимости -> Функции сложного процента
