В конце 60-х гг. уже было известно, что многослойные сети практически лишены недостатков, присущих персептрону. Действительно, если обратиться к рассмотренному выше примеру, нейрон дополнительного слоя вводит новую разделяющую прямую (поверхность) в пространстве параметров, что позволяет образовать различные замкнутые области. [c.131]
Отличительной чертой нейросетей является глобальность связей. Базовые элементы искусственных нейросетей - формальные нейроны - изначально нацелены на работу с широкополосной информацией. Каждый нейрон нейросети, как правило, связан со всеми нейронами предыдущего слоя обработки данных (см. Рисунок 3. иллюстрирующий наиболее широко распространенную в современных приложениях архитектуру многослойного персептрона). В этом основное отличие формальных нейронов от базовых элементов последовательных ЭВМ - логических вентилей имеющих лишь два входа. В итоге, универсальные процессоры имеют сложную архитектуру, основанную на иерархии модулей, каждый из которых выполняет строго определенную функцию. Напротив архитектура нейросетей проста и универсальна. Специализация связей возникает на этапе их обучения под влиянием конкретных данных. [c.43]
В немалой степени популярность персептронов обусловлена широким кругом доступных им задач. В общем виде они решают задачу аппроксимации многомерных функций, т.е. построения [c.50]
Причина популярности персептронов кроется в том, что для своего круга задач они являются во-первых универсальными, а во-вторых - эффективными с точки зрения вычислительной сложности устройствами. В этой главе мы затронем оба аспекта. [c.51]
Возможности многослойных персептронов [c.51]
Изучение возможностей многослойных персептронов удобнее начать со свойств его основного компонента и одновременно простейшего персептрона - отдельного нейрона. [c.51]
Не вдаваясь в излишние подробности резюмируем результаты многих исследований аппроксимирующих способностей персептронов. [c.53]
Градиентное обучение многослойных персептронов [c.57]
Исторически наибольшую трудность на пути к эффективному правилу обучения многослойных персептронов вызвала процедура эффективного расчета градиента функции ошибки dE/t%v. [c.58]
Наши недостатки, как известно - продолжения наших достоинств. И упомянутая выше универсальность персептронов превращается одновременно в одну из главных проблем обучающихся алгоритмов, известную как проблема переобучения. [c.63]
Как и в случае с персептронами начать изучение нового типа обучения лучше с простейшей сети, состоящей из одного нейрона. [c.71]
Эту же ситуацию можно описать и по-другому. Представим себе персептрон с одним (здесь -линейным) нейроном на скрытом слое, в котором число входов и выходов совпадает, причем веса с одинаковыми индексами в обоих слоях одинаковы. Будем учить этот персептрон воспроизводить в выходном слое значения своих выходов. При этом дельта-правило обучения верхнего (а тем самым и нижнего) слоя примет вид правила Ойа [c.73]
Сеть радиального базиса напоминают персептрон с одним скрытым слоем, осуществляя нелинейное отображение RJ => R" у = . ф , . х), являющееся линейной [c.86]
| Рисунок 15. Глобальная (персептроны) и локальная (сети радиального базиса) методы аппроксимации |  |
Подобная возможность раздельного обучения слоев является основным достоинством сетей радиального базиса. В целом же области применимости персептронов и сетей радиального базиса коррелируют с найденными выше областями эффективности квантования и понижения размерности (см. Рисунок 11). [c.87]
В сети из четырех нейронов не реализуемы уже 40 наборов векторов, но все они могут быть получены всего из двух независимых наборов преобразованием однотипности -перестановками переменных и инверсией.4 Такая тенденция является обнадеживающей с точки зрения возможностей сетей к запоминанию образов, поскольку доля не реализуемых функций падает. Однако сети, аттракторы которых сконструированы заранее, могут имитировать только ассоциативную память, не создающую новой информации. Нас же сейчас интересует как раз эффект обобщения, присущий рекуррентным сетям, также как и обычным персептронам. [c.101]
Предложенная ими модель относится к классу растущих нейронных сетей. Такие сети по-своему решают задачу адаптации своей структуры к требованиям решаемой задачи. Вспомним многослойные персептроны, для которых количества скрытых слоев и нейронов в них часто выбираются методом проб и ошибок. Как уже отмечалось в связи с этим, имеются два подхода к адаптивному выбору архитектуры нейросетей. В первом подходе заведомо избыточная нейросеть прореживается до нужной степени сложности. Растущие сети, напротив, стартуют с очень простых и небольших структур, которые разрастаются и усложняются по мере необходимости. [c.118]
Таким образом, в общем случае для получения матрицы весов требуется решить систему линейных уравнений. Но для предварительно выбеленных входов имеем Z = Ski, так что в этом случае матрица кросс-корреляций просто совпадает с матрицей весов обученного линейного персептрона S 7 = wy . [c.140]
Задача состоит в классификации некоторого набора данных с помощью многослойного персептрона и последующего анализа полученной сети с целью нахождения классифицирующих правил, описывающих каждый из классов. [c.169]
Обучение нейронной сети. На этом первом шаге двухслойный персептрон тренируется на обучающем наборе вплоть до получения достаточной точности классификации. [c.169]
| Рисунок 1. Линейная регрессия и реализующий ее однослойный персептрон. | 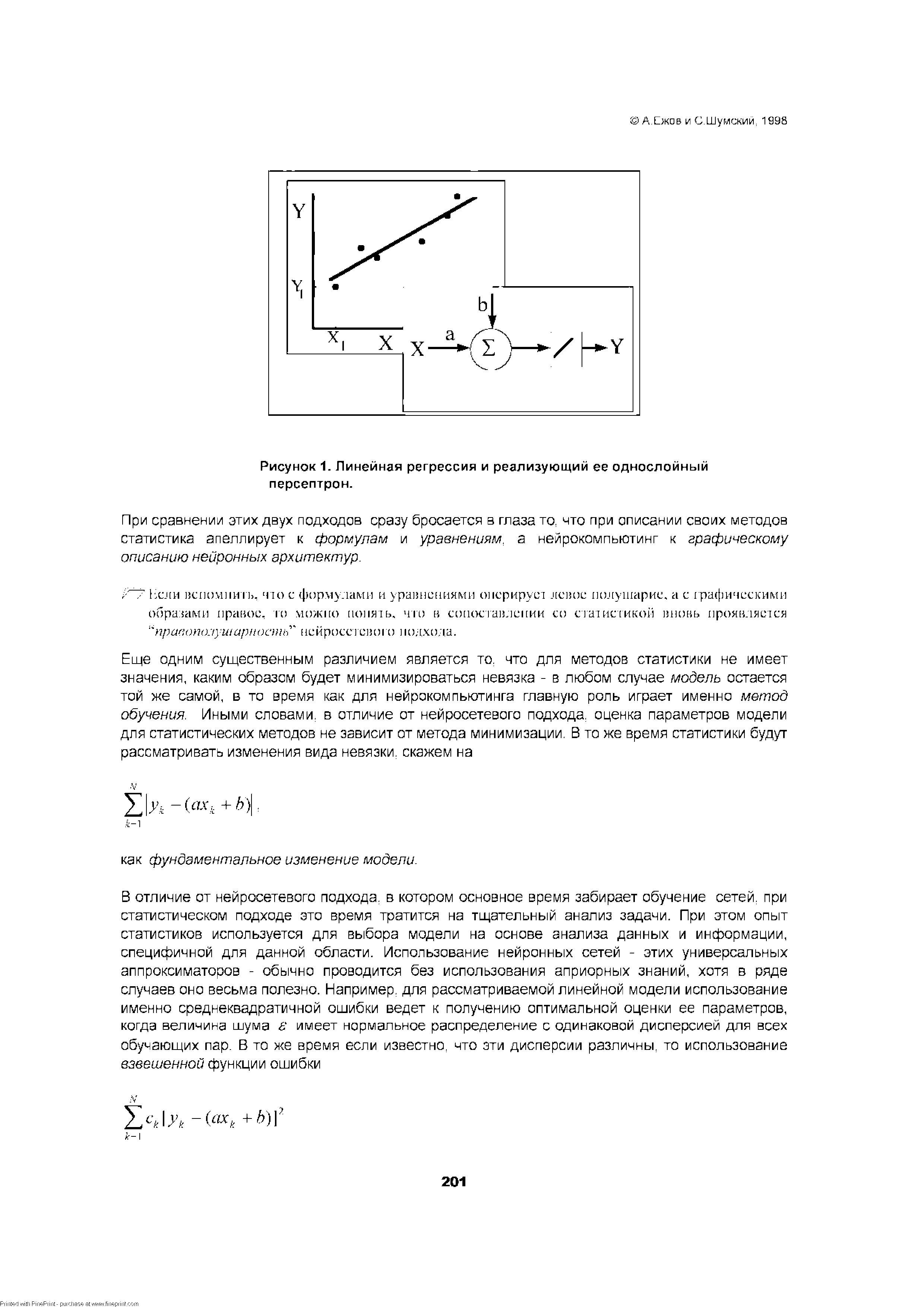 |
В 50-60-х гг. продолжались работы по созданию искусственных нейронных сетей. Одной из первых наиболее важных в этом направлении попыток оказалась работа Ф. Розенблатта, в которой он предложил искусственную нейронную сеть, названную им персептроном. [c.129]
В перестроив имеется один слой искусственных нейронов, на каждый из которых подаются все входные сигналы а( со своими весами Wjj. Такая искусственная нейронная сеть называется однослойной. Схема этой сети достаточно проста, в ней отсутствуют обратные связи с выходов нейронов на их входы, но в этом и ее сила. Именно для такой сети Ф. Розенблатт доказал очень важную теорему о том, что персептрон можно обучить всему, что он способен представить. Смысл этой теоремы состоит в следующем (проблема обучаемости). [c.130]
В 60-е гг. персептрон и его модификации вызвали большой интерес и всплеск оптимизма. Ряд авторов дал убедительные демонстрации систем персептронного типа, и все стремились исследовать возможность этих систем. Однако при этом как-то оставалась в тени проблема представимости, т. е. вопрос о том, что же может и чего не может представлять персептрон. [c.130]
К концу 60-х гг. проблема представимости, т. е. возможности классификации и разделения входных образов на представимые подклассы, была ясно осознана исследователями. В 1969 г. появилась статья М. Минского и С. Пейперта, в которой проблема представимости была строго проанализирована и показано, что имеются жесткие ограничения на то, что могут выполнять персептроны и, следовательно, чему они могут обучиться. В частности, персептрон не способен реализовать функцию исключающее ИЛИ , принимающее выходное значение О при равных значениях двух входов и 1 для всех остальных комбинаций. [c.130]
Без обратных связей Многослойные персептроны (аппроксимация функций, классификация) Соревновательные сети, карты Кохонена (сжатие данных, выделение признаков) [c.48]
Персептропы. Прототипы -задач аппроксимация многомерных функций, классификация образок. Нозмолспости персептронов. Обучение с обратным распространением ошибки. Эффект обобщения и переобучение. Оптимизация размеров сети разрежение связей и конструктивные алгоритмы. [c.50]
Сети о которых пойдет речь в этой главе, являются основной "рабочей лошадкой" современного не и ро компьютинга. Подавляющее большинство приложений связано именно с применением таких многослойных персептронов или для краткости просто персептронов (напомним, что это название происходит от английского per eption - восприятие, т.к. первый образец такого рода машин предназначался как раз для моделирования зрения). Как правило, используются именно сети, состоящие из последовательных слоев нейронов. Хотя любую сеть без обратных связей можно представить в виде последовательных слоев, именно наличие многих нейронов в каждом слое позволяет существенно ускорить вычисления используя матричные ускорители. [c.50]
Исторически, первые персептроны, предложенные Фрэнком Розенблаттом в 1958 г., имели два слоя нейронов. Однако, собственно обучающимся был лишь один, последний слой. Первый (скрытый) слой состоял из нейронов с фиксированными случайными весами. Эти, по терминологии Розенблатта - ассоциирующие, нейроны получали сигналы от случайно выбранных точек рецепторного поля. Именно в этом признаковом пространстве персептрон осуществлял линейную дискриминацию подаваемых на вход образов (см. Рисунок 3). [c.53]
[c.54]
Ключ к обучению многослойных персептронов оказался настолько простым и очевидным, что, как оказалось, неоднократно переоткрывался. [c.58]
Розенблатт трагически погиб, не перенеся тяжелую депрессию, вызванную прекращением финансирования и охлаждением научного собщества к персептронам после выхода в свет книги Минского и Пейперта. [c.58]
Самообучающиеся сети, рассмотренные в этой главе, широко используются для предобработки данных, например при распознавании образов в пространстве очень большой размерности. В этом случае для того, чтобы процедура обучения с учителем была эффективна, требуется сначала сжать входную информацию тем или иным способом либо выделить значимые признаки, понизив размерность, либо произвести квантование данных. Первый путь просто понижает число входов персептрона. Второй же способ требует отдельного рассмотрения, поскольку лежит в основе очень популярной архитектуры - сетей радиального базиса (radial basis fun tions- RBF) [c.86]
Сильной стороной нейроанализа является возможность получения предсказаний при минимуме априорных знаний. Поскольку заранее обычно неизвестно насколько полезны те или иные входные переменные для предсказания значений выходов, возникает соблазн увеличивать число входных параметров, в надежде на то, что сеть сама определит какие из них наиболее значимы. Однако, как это уже обсуждалось в Главе 3, сложность обучения персептронов быстро [c.134]
Заметим, что несмотря на неплохие, в общем-то, результаты, подобные нейросетевые модели весьма компактны. В качестве входных переменных обычно используется от 6 до 10 финансовых индикаторов, являющихся отношением наиболее значимых статей балансов и отчетов о прибылях и убытках корпораций. Например, в последней из упомянутых выше работ первоначально использовались 10 финансовых индикаторов, отобранных аналитиками одного из крупных американских банков. Однако по результатам анализа чувствительности нейросетевых предсказаний к входным переменным два из этих индикаторов оказались незначимыми и не использовались в окончательной модели (8-3-1 персептрон с 3 нейронами на скрытом слое и 1 выходным линейным нейроном, дающим численный эквивалент рейтинга). Качество воспроизведения "тонких" градаций (с учетом субкатегорий, например АА+, АА-) рейтинга агентства Standard Poor s, достигнутое этой моделью, иллюстрирует Рисунок 1. [c.185]
Логистическая регрессия является методом бинарной классификации, широко применяемом при принятии решений в финансовой сфере. Она позволяет оценивать вероятность реализации (или нереализации) некоторого события в зависимости от значений некоторых независимых переменных - предикторов xb...,xN. В модели логистической регресии такая вероятность имеет аналитическую форму Pr(x) =(l+exp(-z ))", где z = ao+ aiXi+...+ aNxN. Нейросетевым аналогом ее очевидно является однослойный персептрон с нелинейным выходным нейроном. В финансовых приложениях логистическую регрессию по ряду причин предпочитают многопараметрической линейной регрессии и дискриминантному анализу. В частности, она автоматически обеспечивает принадлежность вероятности интервалу [0,1], накладывает меньше ограничений на распределение значений предикторов. Последнее очень существенно, поскольку распределение значений финансовых показателей, имеющих форму отношений, обычно не [c.202]
У Очень важной является проблема диагностирования инфаркта миокарда в приемном покое. Опытные врачи правильно определяют это заболевание в 88% случаев и в 29% случаев дают ложную тревогу. Разнообразные статистические методы, включая дискриминантный анализ, логистическую регрессию, рекурсивный анализ распределений и пр. смогли лишь незначительно снизить число ложных тревог (до 26%). А вот Вильям Бакст, работающий на медицинском факультете университета в Сан-Диего, использовал для диагностики многослойный персептрон и повысил число правильно диагностированных инфарктов до 92%. Но более впечатляющим [c.203]

