После преобразования равенства (1.21) условие оптимума потребителя получает следующее выражение [c.34]
На рис 1.12, а показано смещение оптимума потребителя из точки EJ в точку Е2 в результате снижения цены товара X с Рх до Рх". Снижение Рх предопределило поворот бюджетной линии АВ против часовой стрелки вокруг точки А. В результате этого бюджетная линия заняла новое положение АВ и стала касаться в точке Е2 более удаленной кривой безразличия U2. В связи с этим товарный набор Е2 стал доступен данному потребителю. [c.34]
Если соединить одной линией все точки оптимума потребителя, получаемые в результате как снижения, так и повышения Рх, то получим кривую цена—потребление (линия ЕЕ). Она выражает множество оптималь- [c.34]
Поэтому построить линию спроса на новое благо, цена которого на данном этапе еще не известна, с помощью рассматриваемого метода невозможно. На рис. 1.12, б представлена линия индивидуального спроса dd на товар X. Она построена с помощью двух точек L и М, каждая из которых определена исходя из заданной цены и объема спроса, определенного с учетом оптимума потребителя (Е[ и Е2). Линия, проведенная через эти точки (L и М), рассматривается в качестве кривой индивидуального спроса на товар X. Здесь важно также обратить внимание на следующее обстоятельство. Поскольку цена спроса, как было показано в разделе 1.1, имеет отношение не к предельной, а к средней полезности, то и рыночные цены, используемые при построении кривой индивидуального спроса, не могут отличаться по своей природе от цен спроса. [c.35]
Модель равновесие (оптимума) потребителя. [c.5]
Бюджетное ограничение — это геометрическое место точек, представляющих доступные потребителю комбинации товаров при неизменных ценах на них и фиксированном доходе. Если кривые безразличия отражают предпочтения потребителя, то бюджетные линии — его возможности. При расположении на одном графике кривых безразличия и бюджетной линии появляется возможность определить состояние равновесия (оптимума) потребителя точка касания бюджетной линии и наиболее удаленной от начала координат кривой безразличия. [c.103]
В теории производства оптимум производителя определяется аналогично оптимуму потребителя в теории поведения потребителя, т. е. равенством предельной нормы технического замещения одним ресурсом другого и соотношением их цен. [c.112]
В заключение этого пункта заметим, что оптимум потребителя не всегда может быть определен в рамках задачи Лагранжа. Множество допустимых решений ограничено не только бюджетом потребителя, но и условиями неотрицательности объемов благ [c.601]
Пусть при доходе М0 оптимуму потребителя отвечает точка Л0 (рис. 3). Покажем, что при доходе MI = a MO, [c.252]
Раздел 2. Оптимум потребителя 75 [c.75]
Раздел 2. Оптимум потребителя 77 [c.77]
В лекции 15 мы перейдем к решению следующей задачи, стоящей перед теорией поведения потребителя, — изучить, как изменяется оптимум потребителя при изменении границ множества доступных данному потребителю наборов товаров, то есть при изменении дохода и цен. [c.78]
Бюджетная линия. Оптимум потребителя 118 [c.119]
БЮДЖЕТНАЯ ЛИНИЯ. ОПТИМУМ ПОТРЕБИТЕЛЯ [c.119]
Условие оптимума потребителя (3.12) можно интерпретировать следующим образом. Соотношение, в котором потребитель [c.121]
Подставив (3.8) в (3.12), получаем условие оптимума потребителя в следующем виде [c.122]
На рис. 3.10 бюджетная прямая KL ограничена точками К, где X = О, и L, где У = 0. Оптимум потребителя достигается либо в точке К (рис. З.Ю.а), если [c.122]
При данных ценах и доходе оптимум потребителя определяется условием (3.12) (рис. 3.0). Как будет вести себя потребитель при изменении цен и дохода [c.123]
На рис. 3.11 (верхняя часть) показано изменение оптимума потребителя при изменении цены товара X, неизменной структуре предпочтений и прежнем доходе. При снижении РХ до Рх бюджетная линия KL поворачивается вокруг точки К против часовой стрелки и занимает положение КЬ. Покупатель может теперь приобрести больше товара X, если он израсходует на него весь свой доход. В то же время ему становятся доступными все более удаленные от начала координат кривые безразличия. Оптимум потребителя смещается из точки EI в точку 2. Соединяя все подобные точки, получим линию ЕЕ, называемую кривой цена-потребление. Она представляет множество всех оптимальных комбинаций товаров X и У при изменении цены товара X. [c.123]
Рассмотрим теперь изменение оптимума потребителя при изменении его дохода (цены и предпочтения остаются неизменными). С ростом дохода бюджетная линия KL смещается в положение K Li и потребитель переходит на более высокую кривую безразличия U Ui (рис. 3.12). Очевидно, что набор ЕЪ содержит большее количество товаров X и Y, чем набор Е. Со- [c.124]
Разложение общего эффекта изменения цены на эффект дохода и эффект замены по Хиксу показано на рис. 3.16. Бюджетная линия KL соответствует денежному доходу / и ценам РХ и Ру. Ее касание с кривой безразличия U U определяет оптимум потребителя Е, которому соответствует объем потребления товара X в количестве Xi. В случае снижения цены X до PXl и неизменном денежном доходе 7 бюджетная прямая займет положение KL. Она касается более высокой кривой безразличия t/2 2 в точке 2, которой соответствует потребление товара X в объеме Xi. Таким [c.129]
Первоначальному оптимуму потребителя соответствует точка А (<1°х, 9у). текущему — точка В (q x, q, ). [c.152]
Этот вывод иллюстрирует рис. 3.28, подобный рис. 3.27. Здесь оптимум потребителя при /°,р°, оказался в точке С (q , Ду). Хотя набор D (4 ,9у) лежит на той же бюджетной прямой /°/°, потребитель в начальный период предпочитал набор С, поскольку он лежит на более высокой кривой безразличия. [c.153]
| Рис. ЗАЛ. Оптимум потребителя в анализе характеристик. | 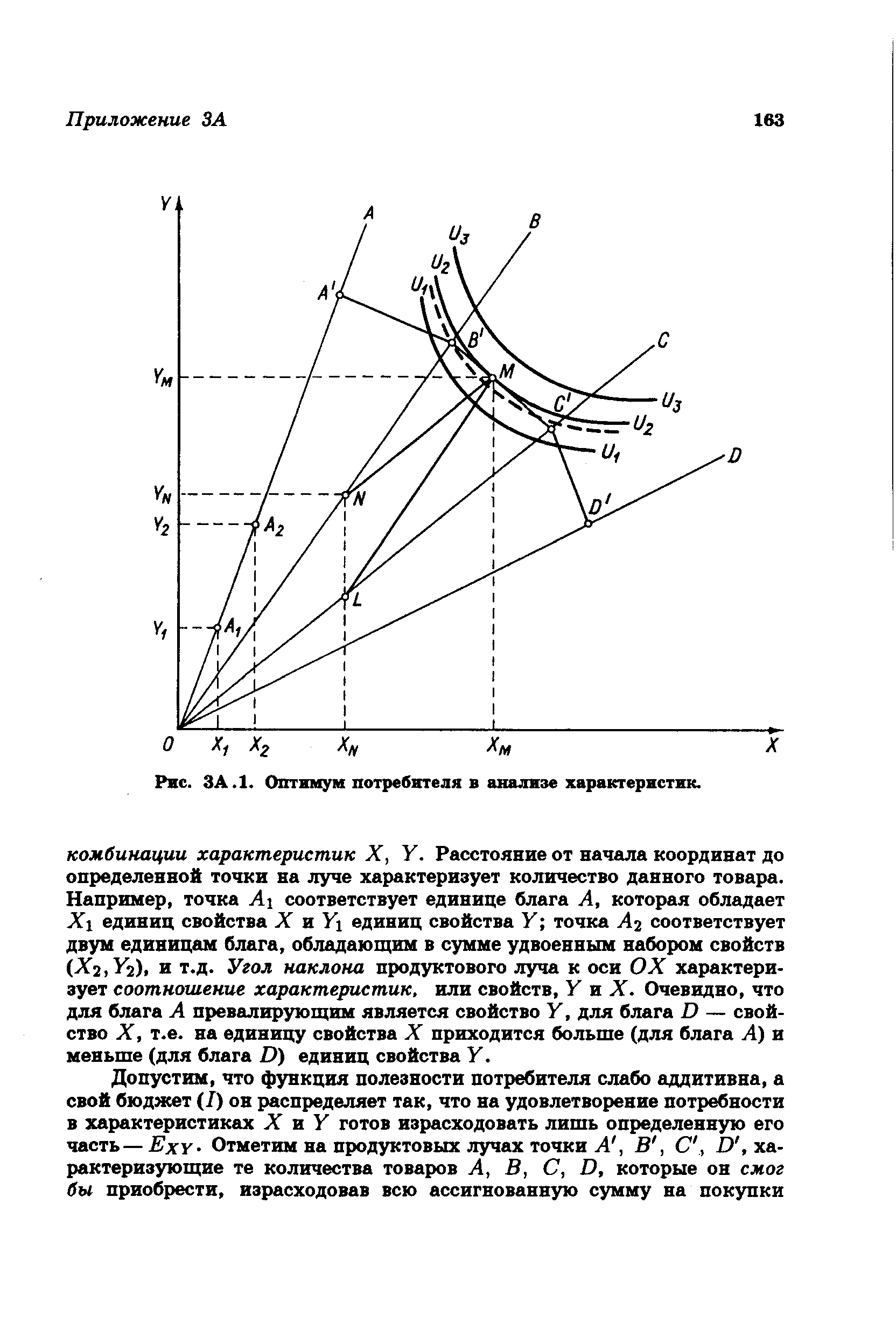 |
Итак, в точке оптимума потребителя отношение предельных полезностей равно отношению цен потребляемых благ. Это условие верно для задачи потребительского выбора с любым числом благ. В соответствии с ним, потребитель распределяет свой денежный доход таким образом, чтобы последняя денежная единица, затраченная на каждый товар, давала одну и ту же предельную полезность. Если бы это было не так, то потребитель мог бы денежную единицу, дающую меньшую предельную полезность, перераспре- [c.131]
Пусть при доходе М0 оптимуму потребителя отвечает точка А0 (рис. 4). Покажем, что при доходе Mj = aM0, где а — любое положительное число, оптимум изображается точкой А, = tA0, лежащей на луче ОА0. [c.697]
Мы знаем, что оптимум потребителя в экономике с ценами достигается тогда, когда МRSjfy - MRS y - РХ/РГ [c.718]
Точки А (рис. 8а) и В (рис. 86) носят название углового решения задачи потребительского выбора в противоположность внутреннему решению (точка Е на рис. 5). Отметим, что если для двухтоварного случая угловое решение является некой особой ситуацией, то для случая достаточно большого числа товаров угловое решение представляет собой скорее правило, чем исключение ведь никто в самом деле не приобретает все те товары, которые предлагает ему рынок. Все же, оставаясь в рамках двухтоварной модели, мы будем в дальнейшем рассматривать, главным образом, внутреннее решение, считая выражение (8) условием оптимума потребителя. [c.78]
Пусть теперь цена товара X снизилась с Рх до Р. В этом случае, как нам уже известно, (см. лекция 14, раздел 1) новая бюджетная линия пересекает ось Оу в той же точке А (цена товара Y не изменилась), а ось Ох — в точке Bj, лежащей правее точки В на оси Ох (цена товара X снизилась). Новая бюджетная линия АВ, имеет точку касания Et с кривой фезразличия ij. Это и есть новый оптимум потребителя. Таким образом, при первоначальной цене потребитель покупает ОХ0 единиц товара X, при новой цене — ОХ1 единиц товара X, т. е. общим эффектом снижения цены является увеличение объема спроса на Х0Х1 единиц товара X. [c.116]
Равенство (3.4) можно интерпретировать следующим образом. Отношение Mt/д/Рд представляет собой прирост общей полезности в результате увеличения расходов потребителя на товар А на 1 руб. Очевидно, что в состоянии оптимума потребителя все подобные отношения для реально покупаемых товаров должны быть равны друг другу. И любое из них может рассматриваться как предельная полезность денег (точнее, 1 руб.). Величина А показывает, на сколько ютилов увеличивается общая полезность при увеличении дохода потребителя на 1 руб. [c.109]
