Приведенные модели выгодны тем, что их параметрам ( ,) можно дать экономическое объяснение (интерпретацию). В линейной модели коэффициенты f ,- показывают, на сколько единиц изменяется результативный показатель с изменением факторного на единицу в абсолютном выражении, в степенных и логарифмических - в процентах. [c.144]
Корреляционная зависимость в отличие от функциональной является неполной, проявляется лишь в среднем и только в массе наблюдений. При корреляционной связи изменению аргумента соответствует несколько значений функций. В зависимости от количества отобранных факторов различают парные и многофакторные модели различного вида линейные, степенные, логарифмические. В практике прогнозирования наибольшее распространение получили линейные модели вида [c.129]
Логарифмически-линейная версия этой модели преобразовывает коэффициент в процентное изменение [c.360]
Модели линейной и логарифмически-линейной регрессии для оценки роста 359-361 Модели риска дефолта 105-110 Модели рыночного риска 102, ПО Модель арбитражной оценки (АРМ) 96, 977-979 Модель диффузных скачков 140 Модель свободных денежных потоков на собственный капитал 465-504 [c.1302]
Изделия-представители Экономико-математические модели Логарифмические линейные функции Значение [c.529]
Логарифмические (лог-линейные) модели [c.180]
В качестве трех альтернативных моделей для проверки гипотез были использованы линейная модель зависимости поступлений подоходного налога от исследуемых видов распределяемых доходов (заработной платы и доходов населения за вычетом социальных трансфертов), логарифмическая модель и модель для эффективной ставки подоходного налога. В рамках этих моделей тесты на прогрессивность социальных платежей представляют собой односторонние тесты на величину коэффициентов, т.е. тесты для проверки гипотезы об отсутствии прогрессивности (регрессивности) налога против гипотезы о прогрессивности (регрессивности). В частности, для исследуемых типов моделей нулевая гипотеза об отсутствии прогрессивности будет предполагать неотрицательность свободного члена в линейной модели, меньшую единицы величину коэффициента при доходах в логарифмической модели и неположительную величину коэффициента при доходах в модели эффективной ставки. [c.283]
Линейная модель Модель эффективной ставки Логарифмическая модель [c.284]
Как и для подоходного налога, в качестве трех альтернативных моделей для проверки гипотез о прогрессивности ЕСН были использованы линейная модель зависимости поступлений подоходного налога от исследуемых видов распределяемых доходов (заработной платы и доходов населения за вычетом социальных трансфертов), логарифмическая модель и модель для эффективной ставки подоходного налога. В рамках этих моделей тесты на прогрессивность социальных платежей представляют собой односторонние тесты на величину коэффициентов, т.е. тесты для проверки гипотезы об отсутствии прогрессивности (регрессивности) налога против гипотезы о прогрессивности (регрессивности). [c.289]
В табл. 4.12 приведены результаты анализа распределения брутто - заработной платы с помощью ЕСН. Прогрессивность можно идентифицировать в том случае, если константа в линейной модели зависимости поступлений ЕСН от заработной платы значима и отрицательна, в модели эффективной ставки - угловой коэффициент значим и положителен и в логарифмической модели - коэффициент при логарифме брутто-доходов превышает единицу. Приведенные оценки показывают, что во всех моделях идентифицирована прогрессивность налога в 2001 и 2002 гг. и отсутствие прогрессивности (и даже регрессивность в логарифмической модели) в 2000 г. [c.289]
В рамках множественной корреляции находятся уравнение регрессии, которые бывают линейными, степенными и логарифмическими. В линейных моделях коэффициенты при неизвестных называются коэффициентами регрессии, а в степенных и логарифмических - коэффициентами эластичности. Первые показывают, насколько единиц изменяется функция с изменением соответствующего фактора на одну единицу при неизменных значениях остальных. Вторые - отражают, на сколько процентов изменяется функция с изменением каждого аргумента на 1 % при неизменных значениях остальных. [c.15]
Модель предполагает, что между независимой величиной W (рекламные расходы) и зависимой X (сбыт или доля рынка) существует простая линейная связь. На практике это весьма проблематично, поэтому логарифмические и [c.89]
Линейно-логарифмическая модель [c.184]
Рассмотрим так называемую линейно-логарифмическую модель [c.185]
| Рис. 156. Население мира и мировой ВНП (GDP) за более, чем 2000 лет от 0 до настоящего времени в логарифмическом масштабе, как функция времени (линейный масштаб). При этом прямая линия означала бы экспоненциальный рост. Восходящее искривление обоих временных рядов показывает, что их рост не может быть объяснен показательной моделью и "суперэкспоненциален". | 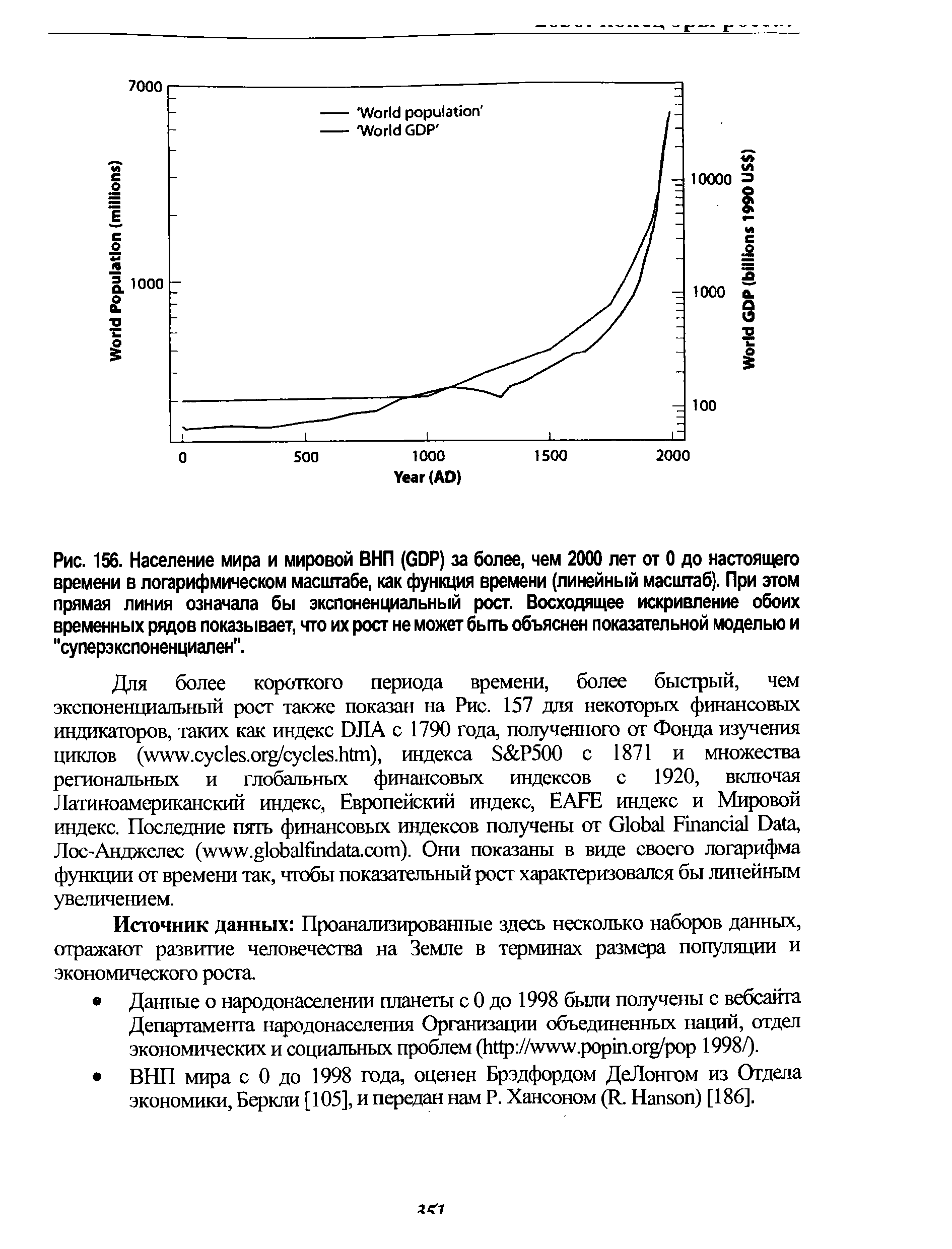 |
Наша первая задача — перевести эти положения на матем. кий язык. И тут мы немедленно сталкиваемся с неожиданным образием открывающихся перед нами возможных способов у ворения сформулированным априорным требованиям теорети кие соотношс ния выбрать между переменными — линейные ил нейные Есл i остановиться на нелинейных, то какими они быть — логарифмическими, полиномиальными или какими-лис Даже определив форму конкретного соотношения, мы оставл нерешенной проблему выбора для различных уравнений заг. ний по времени. Будут ли, например, инвестиции текущего реагировать только на национальный доход, произведенный в нем периоде или же на них скажется динамика нескольких г щих периодов Обычный выход из этих трудностей состоит Е при первоначальном анализе наиболее простой из возможны этих соотношений. Тогда появляется возможность записать ве указанных выше положений следующую модель [c.12]
Смотреть страницы где упоминается термин Логарифмические (лог-линейные) модели
: [c.360] [c.399] [c.359] [c.180] [c.202] [c.35]Смотреть главы в:
Вводный курс эконометрики -> Логарифмические (лог-линейные) модели
