Что понимается под индивидуальными и сводными индексами цен [c.253]
ИНДЕКС ЦЕН — показатель изменения цен на товары или тарифов на услуги за определенный период времени. Различают индивидуальный и сводный индексы цен. Индивидуальный индекс цен — отношение цены на какой-либо товар в отчетном году к цене на тот же товар в базисном периоде. Сводный индекс цен — отношение стоимости группы товаров, реализованных в отчетном периоде, исчисленной в фактических ценах, к ценам базисного периода. [c.246]
Индивидуальные и сводные индексы [c.108]
Различают индивидуальные и сводные индексы. Индивидуальные индексы характеризуют соотношения явлений, которые в данном рассмотрении считаются элементарными, однородными. [c.108]
Эти отношения есть не что иное, как индивидуальные индексы, и сводный индекс представляет собой средний из них [c.370]
По степени охвата явления индексы бывают индивидуальные и сводные. Индивидуальные индексы служат для характеристики изменения отдельных явлении или элементов сложного явления. Их примером могут быть изменения объема производства отдельных видов продукции (зерна, молока и т.д.), а также цен на них. [c.92]
Различают индивидуальные и общие индексы физического объема промышленного производства. Индивидуальные отражают изменение выпуска одного продукта, общие (сводные) индексы физического объема промышленного производства характеризуют Совокупные изменения массы материальных благ, включающей в себя несколько видов продукции. Данный индекс показывает увеличение стоимости всей продукции в результате изменения только ее физического объема при исключении влияния динамики цен. , ..-. [c.274]
Индивидуальные, групповые и сводные индексы [c.108]
Сводные индексы количеств могут иметь случайные погрешности по тем же причинам, что и сводные индексы цен (см. раздел 2.9). Во-первых, иметь случайные погрешности могут индивидуальные индексы количеств. Это может быть обусловлено неполной сопоставимостью данных по кругу отчитывающихся предприятий, проблемами измерения теневой экономики, ошибками сбора и обработки информации и многими другими причинами. Во-вторых, веса, с которыми индивидуальные индексы агрегируются в сводный, могут иметь случайные погрешности, что приводит к возникновению случайных погрешностей и у сводного индекса. Интенсивные струк- [c.145]
Вычислите а) индивидуальные индексы цен и объема продаж по каждому товару б) сводный индекс цен в) сводный индекс объема продаж (физического объема). [c.591]
Мы познакомились с построением сводных индексов на основе индивидуальных. Однако возможен и другой путь. Обратимся к формулам индексов Ласпейреса (10.5) и Пааше (10.7). Эти индексы могут быть рассчитаны на основе данных о количестве проданных товаров в базисном и отчетном периоде (по каждому /-му товару) qnj и qtj и ценах — PIJ и/fy. Такие индексы принято называть агрегатными. Так же можно построить и 1Ч не через осреднение индивидуальных индексов, а на основе сравнения двух сумм (агрегатов), см. (10.7). [c.379]
Индекс называется простым (синонимы частный, индивидуальный), если исследуемый признак берется без учета связи его с другими признаками изучаемых явлений и сводным (синонимы общий, аналитический), если исследуемый признак берется не изолированно, а в связи с другими признаками, например по нескольким логически сопрягаемым элементам. [c.114]
Необходимость в расчете сводных индексов обусловлена тем обстоятельством, что большинство экономических явлений многоаспектны и достаточно сложны. Так, характеризуя экономическую ситуацию, можно оценивать, например, изменение цены на какой-то отдельный, наиболее важный товар, а можно анализировать изменение цен в среднем. Последний случай как раз и иллюстрирует надобность в оценке соотношения некоторых усредненных характеристик анализируемого явления изменение цены на конкретный вид товара описывается индивидуальным индексом цен, на всю номенклатуру товаров или некоторую потребительскую корзину — сводным индексом цен. [c.115]
БЕТА-КОЭФФИЦИЕНТ (или бета) — показатель, характеризующий уровень изменчивости курса котировки отдельного инвестиционного инструмента (ценной бумаги) или их портфеля по отношению к динамике сводного индекса цен всего инвестиционного (фондового) рынка. Бета-коэффициент измеряет уровень как индивидуального, так и портфельного систематического риска. Чем выше значение бета-коэффициента, тем выше уровень систематического и общего риска по конкретному инвестиционному инструменту или их портфелю в целом. [c.149]
Статистики капиталистических стран индексы физического объема исчисляют по данным, характеризующим изменения уровня производства ограниченного числа товаров, являющихся характерными как для отчетного, так и для базисного периода. Набор товаров-представителей, на основе которых строятся индивидуальные динамические ряды, остается неизменным для всего индексируемого периода. Однородные по своему экономическому назначению товары-представители за отчетный и базисный период, выраженные в неизменных ценах, являются стоимостным агрегатом, на базе их определяется, отраслевой индекс. Отраслевые индексы агрегируются в сводный индекс с помощью относительных показателей, характеризующих долю отрасли в общей стоимости, добавленной обработкой. [c.600]
ИНДЕКС ЦЕН - показатель динамики, увеличения или уменьшения цен, характеризующий относительное изменение цен за определенный период. Различают индивидуальный И.Ц., равный отношению цены на данный товар в наблюдаемом (отчетном) году и в базисном периоде, и сводный И.Ц., равный отношению стоимости группы товаров, проданных в отчетном периоде, исчисленной в фактических ценах и ценах базисного периода. [c.266]
Ценовые индексы — это информационные показатели динамики цен за определенный период, которые,1 в свою очередь, подразделяются на ценовые индивидуальные индексы и ценовые сводные индексы. [c.233]
Индекс цен исторически является одним из первых экономических индексов. Практически задачи индекса цен в основном сводятся к оценке изменений цен во времени (индексы динамики) или в пространстве (территориальные индексы). Построение системы индексов цен базируется на общеметодологических принципах, согласно которым в ней выделяются индивидуальные, сводные индексы и индексы средних цен (тарифов). [c.219]
Индивидуальные индексы цен позволяют решать многие практические задачи, но основной задачей является изучение динамики цен разнородной совокупности товаров и услуг. Эта задача решается с помощью сводных индексов, характеризующих среднее изменение цен изучаемой совокупности товаров и услуг. [c.220]
В статистической практике при расчете сводных индексов цен широко применяются различные модификации агрегатных формул, в частности в виде формул среднеарифметических и среднегармонических с использованием индивидуальных индексов (/). [c.220]
Выражение сводного индекса через индивидуальные (/) позволяет наглядно представить как динамику цен по отдельным товарам, так и их роль в формировании сводного индекса. [c.221]
На базе данных о регистрации тарифов по услугам-представителям определяются индивидуальные индексы по видам сообщения (грузов), которые агрегируются в сводные индексы тарифов по видам транспорта и в целом по всем видам транспорта по модификационной формуле Ласпейреса. [c.234]
Еще одну иллюстрацию масштаба структурных сдвигов в российской переходной экономике дают рис. 4.3, 4.4. Рис. 4.3 демонстрирует масштаб расхождений между различными индексами цен. Видим (рис. 4.3,6), что за короткое время, не превышающее нескольких лет (а порой и за несколько месяцев), расхождения между разными индексами цен могут составлять многие десятки процентов. Это означает, что рост цен на разные виды товаров и услуг различается чрезвычайно сильно. Различные индексы количеств также демонстрируют колоссальный разброс (рис. 4.4), что свидетельствует о принципиально разной динамике производства многих видов товаров и услуг. Особо подчеркнем, что столь значительное рассеяние на рис. 4.3, 4.4 демонстрируют сводные индексы, т. е. средние больших совокупностей индивидуальных индексов, хотя средние величины по своей природе более стабильны. Заметим, что помимо исключительного масштаба структурных сдвигов это рассеяние может также отражать и проблемы, присущие долгосрочным сопоставлениям, такие, как резкий рост относительной погрешности экономических индексов при столь долгосрочных сопоставлениях. [c.61]
В экономике аналогом материальной точки можно считать элементарное явление. Его изменение описывается индивидуальным индексом. Неоднородное явление - аналог системы материальных точек. Его изменение полностью описывается совокупностью соответствующих индивидуальных индексов. Однако и здесь часто бывает удобнее изменение неоднородного явления как целого описывать единственным сводным индексом. [c.111]
Таким образом, сводные индексы цен Ласпейреса и Пааше могут быть представлены и как отношения стоимостей корзин товаров-представителей в сопоставляемые периоды, и как взвешенные средние (арифметические или гармонические) индивидуальных индексов цен. Соответственно их можно интерпретировать и как изменение стоимости корзины, и как меру расположения распределения индивидуальных индексов. Аналогично — индексы количеств. [c.115]
Адекватный учет замещения особенно важен в тех случаях, когда точность весов невелика. Так, в последнее время во многих странах осуществлен переход на использование формул на основе геометрического среднего при построении индексов цен элементарных агрегатов, т. е. тех индексов, которые используются в качестве индивидуальных при построении сводного индекса цен. Аналогично такие индексные формулы могли бы быть полезными и на нижнем уровне построения индексов количеств, где точность весов также невелика. [c.122]
Выше уже были отмечены такие соображения, как технологичность, простота интерпретации и адекватный учет замещения более быстро дорожающих товаров относительно дешевеющими. Другие соображения могут быть получены из требования сохранения свойств операций над индексами при переходе от индивидуальных индексов к сводным (и, вообще, на каждый более высокий иерархический уровень в системе экономических индексов). Как уже отмечалось, произведение индивидуального индекса цен на соответствующий индивидуальный индекс количеств дает индивидуальный индекс стоимостей. Соображением, позволяющим предпочесть одни индексные формулы другим, является требование сохранения этого свойства при переходе от индивидуальных индексов к сводным. Это свойство является весьма привлекательным, в частности потому, что сводный индекс [c.122]
Выше обсуждались некоторые соображения, позволяющие предпочесть одни индексные формулы другим. Еще одним соображением является требование выполнения теста обратимости ситуаций, в соответствии с которым индекс, рассчитанный в прямом направлении должен представлять собой обратную величину по отношению к индексу, исчисленному в обратном направлении [51]. При проведении межвременных сопоставлений этот тест называют тестом обратимости во времени. В соответствии с ним для любой пары сопоставляемых периодов t и t2 должно выполняться I(t, t2)-I(t2,ti) — 1. Этот тест всегда выполняется для индивидуальных индексов, но многие формулы сводных индексов ему не удовлетворяют. Из рассмотренных выше, тесту обратимости во времени не удовлетворяют индексы Ласпейреса и Пааше, а индексы Фишера, Эджворта-Маршалла и все индексы, основанные на геометрических средних, этому тесту удовлетворяют. [c.140]
Продемонстрируем это на следующем примере. Пусть корзина состоит всего из двух товаров-представителей - нефти и газа. Добыча нефти почти не подвержена воздействию сезонного фактора (рис. 2.3, о), тогда как добыча газа, напротив, демонстрирует значительные сезонные колебания (рис. 4.7,о). Поэтому, если разные сегменты сцепленного индекса построены с использованием различных весов, то сезонные колебания временного ряда сводного индекса на разных сегментах будут иметь разный масштаб, что усложнит проведение сезонной корректировки и ухудшит качество ее результата. Стандартной рекомендацией в таких случаях является проведение сезонной корректировки временных рядов индивидуальных индексов и построение сезонно скорректированного ряда сводного индекса на их основе. [c.143]
Заметим, что сезонные волны временных рядов сводных индексов могут эволюционировать вне зависимости от того, эволюционируют ли сезонные волны временных рядов индивидуальных индексов, причем это относится не только к сцепленным индексам, но и к прямым, хотя для сцепленных индексов эта проблема более актуальна. [c.145]
Одной из важнейших с измерительной точки зрения особенностей протекания экономических процессов в российской переходной экономике является наличие в ней интенсивных и затяжных структурных сдвигов, состоящих в том, что изменения индивидуальных индексов (например, цен или объемов производства) для разных товаров и услуг могут чрезвычайно сильно различаться. Это порождает весьма серьезные проблемы построения временных рядов сводных экономических индексов, снижая точность сопоставлений, а порой делая проведение сопоставлений лишь на основе сводных индексов не вполне адекватным. Поэтому раздел 4 настоящей работы посвящен анализу структурных сдвигов и структурных различий. Рассмотрен инструментарий анализа структурных сдвигов и структурных различий, являющийся естественным расширением стандартного инстру- [c.10]
Разделение смещений, вызванных замещением, на две группы (для верхнего и нижнего уровней построения индекса цен), обусловлено следующими соображениями. Прежде всего, при построении элементарных агрегатов возникают более серьезные проблемы с формированием систем весов, которые используются в индексных формулах. При построении сводных индексов потребительских цен веса могут быть основаны на информации о структуре потребительских расходов, полученной на базе обследований бюджетов домашних хозяйств. Для построения же элементарных агрегатов необходима гораздо более детализированная информация такого рода, которая обычно бывает известна с гораздо меньшей точностью. Это приводит к тому, что точность весов, используемых при построении элементарных агрегатов, обычно значительно уступает точности весов, используемых при построении сводных индексов цен. Помимо этого, временные ряды индивидуальных индексов цен, на основе которых строятся элементарные агрегаты, имеют большую волатильность по сравнению с временными рядами элементарных агрегатов, используемых при построении сводных индексов цен, поскольку менее агрегированные данные вообще более волатильны по сравнению с соответствующими им агрегированными данными. Все это приводит к тому, что использование одних и тех же индексных формул порождает больше проблем при построении элементарных агрегатов, чем при построении сводных индексов цен. [c.21]
Вместе с тем по целому ряду причин сводные индексы цен (и количеств) могут иметь значительные случайные погрешности. Так, сводный индекс можно представить как некое среднее индивидуальных индексов. При этом веса, с которыми индивидуальные индексы учитываются в сводном, бывают известны с некоторой погрешностью, которая имеет и случайную составляющую. Поэтому различия в индивидуальных индексах цен (т.е. структурные сдвиги) приводят к возникновению случайной погрешности у сводного индекса, причем чем такие различия сильнее, тем больше случайная погрешность. Помимо этого, и индивидуальные индексы цен могут иметь случайную погрешность, что также вносит вклад в случайную погрешность сводного индекса. [c.23]
При широком использовании в экономической практике индивидуальных и сводных индексов цен определенный интерес представляет исчисление индекса динамики средних цен. Средние цены, а следовательно, и индекс средних цен определяются по достаточно однородным группам товаров и при условии, что все товары, входящие в группу, измеряются одинаковыми количественными единицами (тоннами, литрами и т. д.). Средние цены определяются путем деления стоимости (Lpfl) на общее количество изучаемых единиц в группе ( <7,)- [c.225]
Деление на индивидуальные и сводные индексы является условным и зависит от решаемой задачи. Индекс, являющийся сводным в одной задаче, может рассматриваться как индивидуальный в другой. Так, если задача состоит в анализе динамики цен на яблоки всех сортов во всех торговых точках, то соответствующий индекс цен рассматривается как сводный. Если же задача состоит в анализе динамики цен на все потребительские товары и услуги, то этот же индекс цен на яблоки может использоваться как индивидуальный. Сводные индексы, которые, подобно этому индексу цен на яблоки, используются в качестве индивидуальных при построении сводных индексов более высокого уровня, часто называют элементарными агрегатами (elementary aggregates). [c.109]
Использование индивидуальных и сводных индексов предполагает выделение двух иерархических уровней в системе индексов. Часто используют системы индексов с иным количеством иерархических уровней. Когда их три, то говорят об индивидуальных, групповых и сводных индексах. Групповые индексы (т. е. индексы промежуточных иерархических уровней) иногда также называют субиндексами. [c.109]
ИНДЕКС (index) — стат относительный показатель, характеризующий соотношение во времени (дин И ) социально-экон явлений цен отдельных товаров, объемов произ-ва разл продукции, себестоимость продукции и т п И делятся на индивидуальные и сводные Индивидуальный И характеризует изменение отдельных явлений во времени цены на определенный товар, выплавки стали, урожайности картофеля и т д Для вычисления индивидуального И величину явления в отчетном периоде делят на величину его в предшествующем периоде Сводный И служит для сопоставления непосредственно несоизмеримых, разнородных явлений Чтобы сделать такие явления сопоставимыми, необходимо несоизмеримые явления (их составные элементы) сделать соизмеримыми, выразить их общей мерой стоимостью, трудовыми затратами и т д Показатель, изменение которого определяется, называется индексируемым, а связанный с ним и принимаемый за неизменный — весом В ст-ке принята след система условных обозначений в И q — кол-во произведенной млн реализованной продукции в натуральном выражении, р — цена ед продукции, г — себестоимость продукции, t — трудоемкость продукции, b — [c.84]
В условиях масштабных структурных сдвигов обычная практика индексного анализа, состоящая в замене всей совокупности индивидуальных индексов единственным сводным, далеко не всегда бывает адекватной. Такая замена допустима лишь при небольшом разбросе индивидуальных индексов, при этом что такое "небольшой разброс" определяется той задачей, для решения которой используется индекс. В случае значительных структурных сдвигов может потребоваться использование дополнительной информации о совокупности индивидуальных индексов. С этой целью можно, помимо меры расположения, анализировать также другие числовые характеристики распределений индивидуальных индексов - меры рассеяния, асимметрии, эксцесса и т. д. Либо можно использовать для анализа, помимо сводного, еще и групповые индексы. При таком масштабе структурных изменений анализ лишь сводного экономического индекса, т. е. лишь среднего значения совокупности индивидуальных индексов (как бы оно ни было определено), может быть недостаточен для описания изменения всей совокупности индивидуальных индексов15. [c.62]
| Рис. 6.4. Иллюстрация возникновения экспоненциального смещения при построении временного ряда сцепленного индекса по осциллирующим индивидуальным индексам с использованием индексной формулы, не удовлетворяющей тесту обратимости во времени 1 и 2 - индивидуальные индексы 3 - сводный индекс | 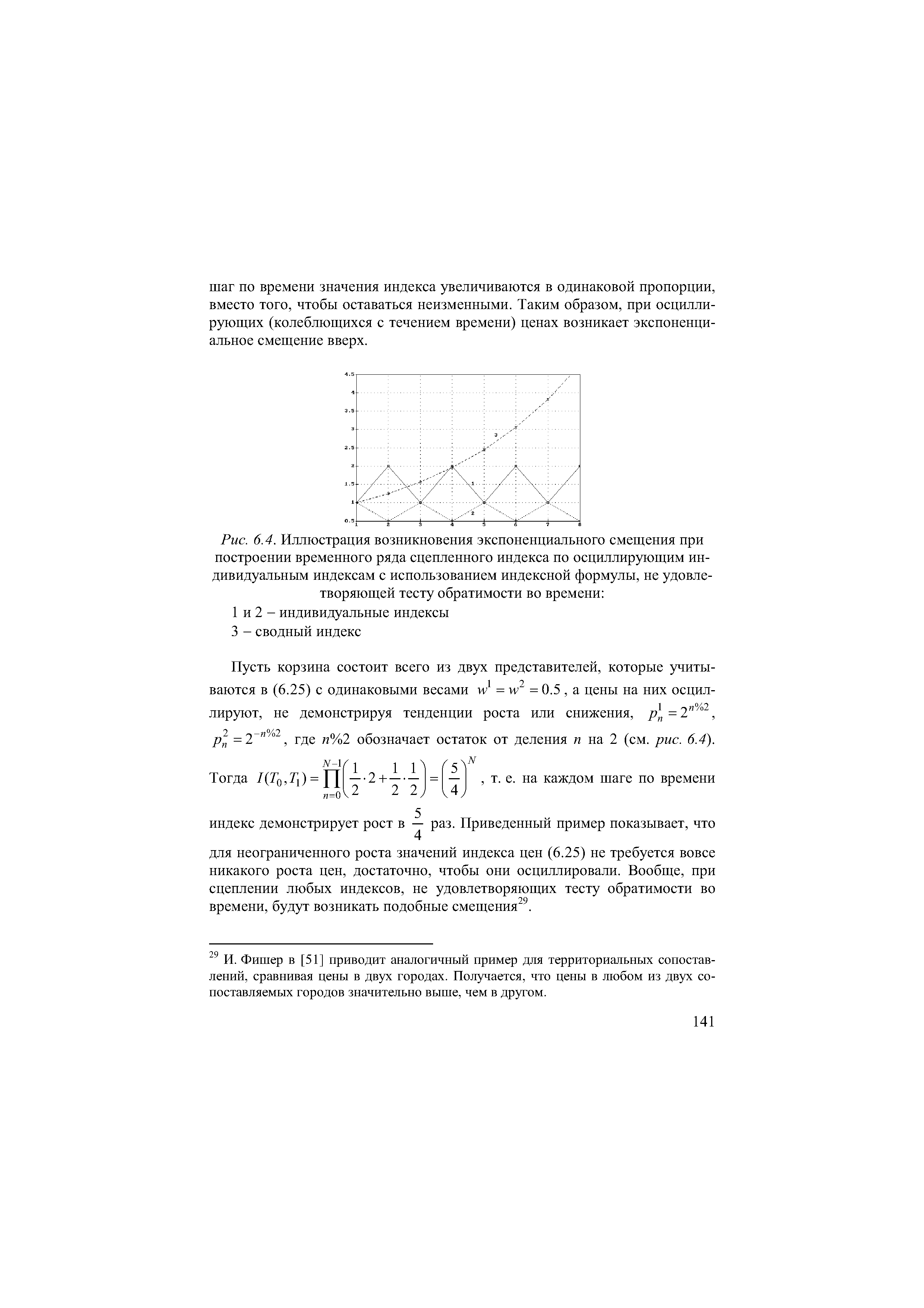 |
