Применение технологических операций по параметризации компонентов СМОД обеспечивает простоту привязки ТПР к конкретным условиям объекта управления, повышает уровень их адаптивности. [c.122]
Параметризация компонентов СМОД 31 [c.244]
| Рисунок 7. Анализ главных компонент дает линейное подпространство, минимизирующее отклонение данных (а). Он не способен, однако, выявить одномерный характер распределения данных в случае (Ь). Для их одномерной параметризации нужны нелинейные координаты. | 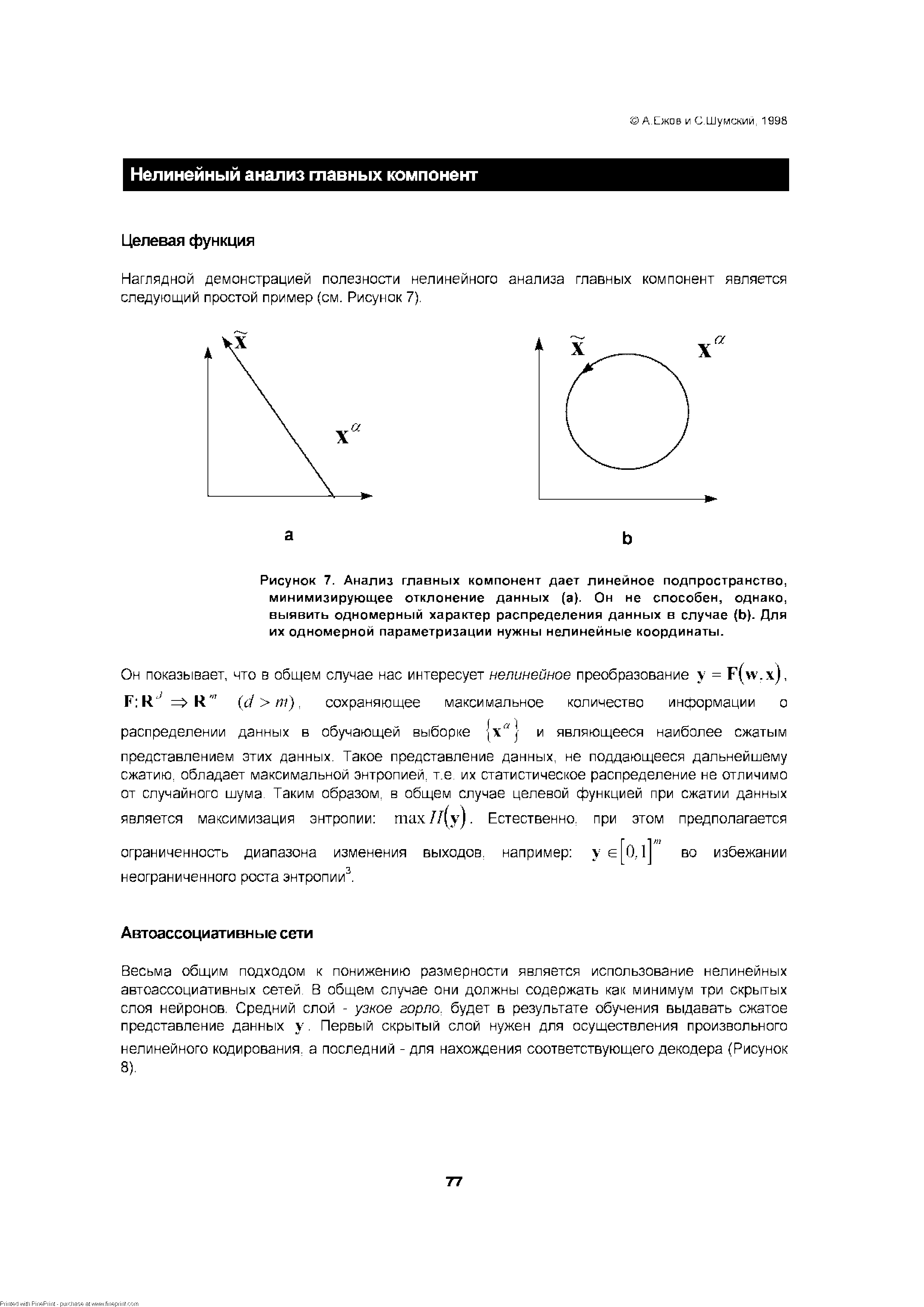 |
Рассмотренные выше общие методические положения создания и применения комплекса профилей ИС следует детализировать для каждого профиля до уровня Руководящих указаний по адаптации и параметризации и Методик по применению для конкретных проблемно-ориентированных областей или конкретных проектов ИС. В этих документах должны быть представлены конкретные операции, структура и содержание документов, обеспечивающих регламентированное применение профиля и контроль соответствия процессов и объектов ИС требованиям и рекомендациям профиля. Положения каждой методики и сценарии их конкретного применения необходимо поддержать технологией и средствами автоматизации их реализации, документирования и контроля соответствия утвержденному профилю. Для создания руководящих указаний и методик применения профилей при подготовке к проектированию ИС следует утвердить их номенклатуру и требования к содержанию. Дальнейшие работы организовывают для создания конкретных методик применения каждого профиля в тесном взаимодействии с подразделениями, которым предстоит использовать соответствующие профили. Такие методики должны предусматривать длительное развитие, расширение и модернизацию функций компонентов и ИС в целом. С этой целью организуют учебные курсы для специалистов по применению и контролю соблюдения положений каждого профиля. [c.84]
Значения экономических переменных определяются обычно влиянием не одного, а нескольких объясняющих факторов. В таком случае зависимость у =Дх) означает, что х - вектор, содержащий т компонентов х = (х,, х2,. .., хт). Задача оценки статистической взаимосвязи переменных у и х"= (х(, х,,. .., хга) формулируется аналогично случаю парной регрессии. Записывается функция у = Да,х)+е, где а - вектор параметров, е - случайная ошибка. Предполагается, что эта функция связывает переменную у с вектором независимых переменных х для данных генеральной совокупности. Как и в случае парной регрессии, предполагается, что ошибки е являются случайными величинами с нулевым математическим ожиданием и постоянной дисперсией е( и е статистически независимы при ij. Кроме того, для проверки статистической значимости оценок а обычно предполагается, что ошибки е( нормально распределены. Поданным наблюдений выборки размерности л требуется оценить значения параметров а, то есть провести параметризацию выбранной формулы (спецификации) зависимости. [c.307]
Выполнение всех этих операций завершается составлением ТЭО (Д7.1) и формированием ТЗ (Д7.2) на операции П7. Целью разработки Технико-экономического обоснования проекта ЭИС являются оценка основных параметров, ограничивающих проект ЭИС, обоснование выбора и оценка основных проектных решений по отдельным компонентам проекта. При этом различают организационные параметры, характеризующие способы организации процессов преобразования информации в системе, информационные и экономические параметры, характеризующие затраты на создание и эксплуатацию системы, экономию от ее эксплуатации. Основными объектами параметризации в системе являются задачи, комплексы задач, экономические показатели, процессы обработки информации. [c.68]
Параметризация позволяет определить требования к системе, оценить существующую информационную систему, определить пригодность типовых решений в проекте ЭИС, выбрать проектные решения в соответствии с предъявляемыми требованиями к ЭИС. К основным компонентам ТЭО относятся [c.69]
Один из распространенных подходов к прогнозированию состоит в следующем ряд раскладывается на долговременную, сезонную (в том числе, циклическую) и случайную составляющие затем долговременную составляющую подгоняют полиномом, сезонную — рядом Фурье, после чего прогноз осуществляется экстраполяцией этих подогнанных значений в будущее. Однако этот подход может приводить к серьезным ошибкам. Во-первых, короткие участки стационарного ряда (а в экономических приложениях редко бывают достаточно длинные временные ряды) могут выглядеть похожими на фрагменты полиномиальных или гармонических функций, что приведет к их неправомерной аппроксимации и представлению в качестве неслучайной составляющей. Во-вторых, даже если ряд действительно включает неслучайные полиномиальные и гармонические компоненты, их формальная аппроксимация может потребовать слишком большого числа параметров, т.е. получающаяся параметризация модели оказывается неэкономичной. [c.48]
