Взаимодействие нейронов анализ главных компонент [c.74]
Действительно, для этих целей существуют хорошо известные алгоритмы стандартного статистического анализа. В частности. анализ главных компонент также выделяет основные [c.75]
Нелинейный анализ главных компонент [c.77]
Наглядной демонстрацией полезности нелинейного анализа главных компонент является следующий простой пример (см. Рисунок 7). [c.77]
| Рисунок 7. Анализ главных компонент дает линейное подпространство, минимизирующее отклонение данных (а). Он не способен, однако, выявить одномерный характер распределения данных в случае (Ь). Для их одномерной параметризации нужны нелинейные координаты. | 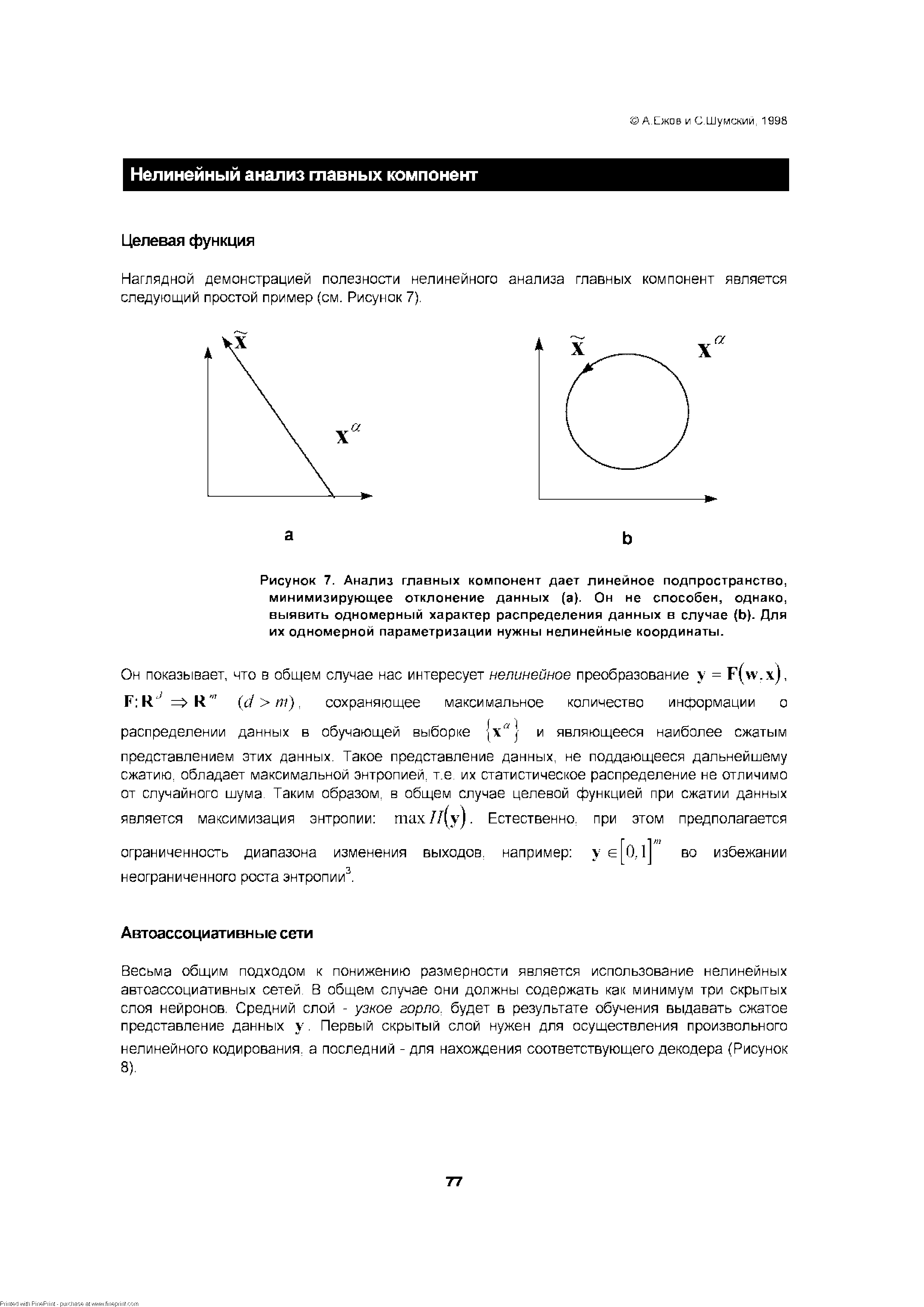 |
С помощью нелинейного анализа главных компонент (АГК) мы не только преобразовали буквенные и порядковые переменные в числовые, но и уменьшили размерность множества данных с 26 (число переменных) до 5 (число значимых факторов). После этого, конечно, становится труднее представить себе суть этих новых составных переменных и понять, какое влияние каждая из них оказывает на результаты классификации. При АГК для каждого наблюдения вычисляются определенные числовые показатели этого объекта в каждом значимом измерении. Эти показатели (которые можно назвать количественными выражениями того, обладает ли объект тем или иным свойством) и используются в качестве входных данных для MDA. В итоге АГК дает новый набор данных меньшей размерности, чем у исходного (5 вместо 26), где уже все переменные являются числовыми. Конечно, эти два набора данных тесно связаны, поскольку [c.176]
Анализ главных компонент [c.189]
При наличии 49 переменных и 30 наблюдений возникает проблема, связанная с числом степеней свободы.. Если число подлежащих оцениванию параметров превышает число наблюдений, то всегда можно достичь абсолютного соответствия модели наблюдаемым данным, но это соответствие будет на самом деле мнимым. Не имея возможности существенно увеличить число наблюдений, мы приняли решение уменьшить число переменных. При помощи нелинейного анализа главных компонент были выделены три наиболее значимых показателя (измерения), на которые приходится большая часть (около 60%) вариаций в исходной базе данных. [c.189]
Голландским инвестиционным банком была разработана и использовалась реальная качественная база данных для оценки будущего состояния дел его корпоративных клиентов. Из-за того, что целевая переменная определялась задним числом, данные не позволяли исследовать ошибки 2-го рода. При помощи нелинейного анализа главных компонент первоначальное количество переменных (49) было уменьшено до 19 переменных, которые располагались в трех измерениях. В связи с тем, что, как выяснилось, около 60% исходных переменных несущественны для принятия решения, банк в настоящее время подумывает о том, чтобы изменить способ оценки. Как вариант рассматривается двухступенчатая процедура, в которой клиент сначала проходит сканирование по 19 переменным, а в случае успеха включаются в работу 30 новых переменных. Благодаря такому двухъярусному методу будут высвобождены значительные управленческие ресурсы банка. Малая степень значимости пяти финансовых показателей в полученном трехмерном пространстве может быть связана с тем, что в исследуемой выборке были представлены только жизнеспособные компании. [c.195]
АНАЛИЗ ГЛАВНЫХ КОМПОНЕНТ [c.196]
При использовании анализа главных компонент общая изменчивость данных находится как сумма собственных значений (которая будет равна сумме элементов на главной диагонали С, известной как ее след). Затем компоненты (линейные комбинации переменных) выбираются в порядке убывания собственных значений, пока главные компоненты не будут отвечать за достаточно большую долю изменчивости. Таким образом, размерность системы признаков снижается и определяются наиболее важные компоненты (направления). [c.300]
Анализ главных компонент (АГК) [c.301]
В анализе главных компонент мы извлекали линейные комбинации рассматриваемых переменных так, что на каждой стадии получаемая компонента объясняет наибольшую возможную долю остающейся изменчивости. В ФА мы, по сути, разбиваем совокупную дисперсию данных на две части — на ту, которая разделяется всеми переменными (общность), и ту, которая специфична для каждой отдельной переменной. Факторный анализ использует оценки общности для построения объясняющих факторов. [c.311]
Применение методов факторного анализа требует большой подготовительной работы и трудоемких расчетов по разработке моделей. Поэтому без ЭВМ не рекомендуется применять методы корреляционного и регрессионного анализа, главных компонент, факторного анализа. К тому же в настоящее время для ЭВМ различных классов имеются стандартные программы по этим методам. В свою очередь пользоваться установленными с помощью ЭВМ моделями очень просто. [c.81]
МНОГОМЕРНЫЙ АНАЛИЗ АНАЛИЗ ГЛАВНЫХ КОМПОНЕНТ И ФАКТОРНЫЙ АНАЛИЗ [c.493]
Анализ главных компонент переменных [c.493]
АНАЛИЗ ГЛАВНЫХ КОМПОНЕНТ (АГК) [c.495]
Анализ главных компонент применяется при разработке моделей риска на рынках облигаций. Из гл. 3 мы помним, что дюрация и выпуклость широко используются участниками рынка облигаций для обобщения чувствительности отдельных облигаций и портфелей облигаций к изменениям процентных ставок. Однако как дюрация, так и выпуклость облигации основываются на допущении, что кривая доходности является твердой и может переноситься только параллельно. Случайный эмпиризм показывает, что эти допущения в действительности не имеют места. На практике отдельные спот-курсы не обладают идеальной корреляцией, таким образом, временная структура и отсюда кривая доходности не переносятся параллельно. [c.504]
Объясните, как вы понимаете понятия "факторный анализ" и "анализ главных компонент". Определите разницу между двумя процессами. [c.517]
Что такое собственные векторы и собственные значения Каково их значение в факторном анализе и анализе главных компонент. [c.518]
Объясните, как использовать стандартизованные переменные в анализе главных компонент. [c.518]
Сравнивая два способа решения систем (8.60) (непосредственно с матрицей X и с переходом к системе нормальных уравнений), можно сделать вывод, что несогласованные системы (8.60), как правило, лучше решать, используя переход к нормальной системе уравнений. В статистической практике несогласованные системы возникают, когда матрица данных X переопределена, т. е. число объектов (столбцов) в ней больше числа переменных (строк), и при этом линейные уравнения, входящие в систему (8.60), не могут выполняться точно. Но превышение числа объектов над числом переменных — типичная ситуация в регрессионном анализе. Второе условие несогласованности также часто выполняется, так как обычно системы линейных уравнений используются для оценки параметров линейных моделей типа (8.1), являющихся лишь приближением действительных соотношений между переменными (мерой этого приближения как раз и является дисперсия случайной компоненты е). Для обоснования перехода к нормальной системе уравнений существенно и то, что матрица Х Х тесно связана с ковариационной матрицей, которая является исходным объектом для различных видов многомерного анализа (главных компонент, факторного анализа и т. д.). [c.275]
При дисперсионном (глава 16), регрессионном (глава 17) и дискриминантном анализе (глава 18) одну переменную маркетологи четко идентифицируют как зависимую. Теперь же рассмотрим, как проводится факторный анализ, не предполагающий разделение переменных на независимые и зависимые. Наоборот, исследователи проверяют все возможные варианты взаимозависимостей между переменными. В этой главе обсуждается основная концепция факторного анализа и дается понятие факторной модели. Мы опишем этапы факторного анализа и проиллюстрируем их с точки зрения анализа главных компонент и анализа общих факторов. Для начала приведем несколько примеров, иллюстрирующих полезность факторного анализа. [c.717]
Как потребители оценивают банки Респондентов попросили важность 15 банковских характеристик по пятибалльной шкале — от несущественной характеристики до очень важной, данные были изучены с помощью анализа главных компонент. [c.717]
Однако стандартный анализ главных компонент дает решение в явном виде, через последовательность матричных операций, а не итерационно, как в случае нейросетевых алгоритмов. Так что при отсутствии высокопараллельных нейроускорителей на практике удобнее пользоваться матричными методами, а не обучать нейросети. Есть ли тогда практический смысл в изложенных выше итеративных нейросетевых алгоритмах [c.76]
Подобные правила рассчитаны на то, чтобы сеть начинала свою работу в линейном режиме и притом не на плоской части поверхности невязок. Однако нет гарантии, что такое начальное приближение приведет к глобальному минимуму или уменьшит время сходимости. Были разработаны другие методы, дающие еще более хорошее начальное приближение с точки зрения уменьшения времени обучения и обладающие большей устойчивостью в смысле локальных минимумов. Так, Дено и Ланжель разработали метод инициализации весов по прототипам, полученным из обучающего множества ]. Усовершенствованный классический метод выбора начальных значений использует данные анализа главных компонент, но для этого, безусловно, требуется меньше скрытых элементов, чем имеется входов [292]. При использовании обучающих алгоритмов типа ВР выбор начального приближения очень важен. Уже на этом шаге нужно позаботиться о том, чтобы не попасть в локальный минимум. [c.30]
Для обработки данных использовалась MBPN-сеть с логистическими функциями активации. Предполагалось, что после обучения сеть будет в состоянии правильно классифицировать новые (незнакомые ей) компании. В качестве исходной точки для сравнений была взята обычная линейная MDA-модель. Однако для метода MDA требуется, чтобы переменные были числовыми, — с буквенными или порядковыми переменными он работать не может. Проблема сведения всех показателей к числовым была решена при помощи нелинейного анализа главных компонент. [c.176]
Анализ главных компонент и факторный анализ — это методы анализа структуры данных в рамках многофакторности. Эти методы вместе с методом множественной регрессии наиболее часто используются в многофакторном анализе. В случае анализа главных компонент и факторного анализа, в отличие от регрессионного, исследующего взаимосвязь эндогенных переменных с экзогенными, исследуется взаимоотношение только между эндогенными переменными. (Эндогенными называются внутренние факторы системы, а экзогенными — внешние.) [c.298]
Аналич гттавных компонент и факторный анализ — это методы анализа структуры данных в рамках многофакторности. Вместе с множественной регрессией (см. гл. 6) и многофакторной корреляцией в рядах динамики (см. гл. 8) эти методы наиболее часто используются в многофакторном анализе. Они отличаются от множественной регрессии тем, что целью регрессии является определение связи между экзогенной переменной и множеством эндогенных переменных. В случае анализа главных компонент и факторного анализа исследуется взаимоотношение только между эндогенными переменными. В отличие от корреляции в рядах динамики отношения между эндогенными переменными не обязательно должны быть устойчивыми. [c.493]
Анализ главных компонент представляет собой скорее средство, чем цель. Например, определение главных компонент может служить для построения уравнения регрессии, так что зависимая переменная регрессируется не по первичным независимым переменным, а по главным компонентам. Далее в этой главе мы увидим, как определение главных компонент в изменениях процентных ставок позволяет нам лучше измерить процентный риск портфелей облигаций. [c.496]
Анализ главных компонент относится к линейным комбина-циям переменных, и из гл. 1 мы знаем, что цены облигаций представляют собой линейную комбинацию текущих стоимо-стей. Каждая текущая стоимость — это результат применения соответствующей спот-ставки для приведения денежного потока. Мы можем использовать метод главных компонент для определения линейных комбинаций изменений текущих стоимостей в результате изменения процентных спот-ставок. На основе линейных комбинаций изменений текущих стоимостей очень просто соотнести их с комбинациями изменений спот-ставок, которые явились причиной изменения текущей стоимости. [c.506]
Смотреть страницы где упоминается термин Анализ главных компонент (АГК)
: [c.70] [c.145] [c.202] [c.169] [c.249] [c.251] [c.299] [c.494] [c.504] [c.131] [c.126] [c.429] [c.320] [c.670]Смотреть главы в:
Количественные методы в финансах -> Анализ главных компонент (АГК)
