| Рисунок 7. Анализ главных компонент дает линейное подпространство, минимизирующее отклонение данных (а). Он не способен, однако, выявить одномерный характер распределения данных в случае (Ь). Для их одномерной параметризации нужны нелинейные координаты. | 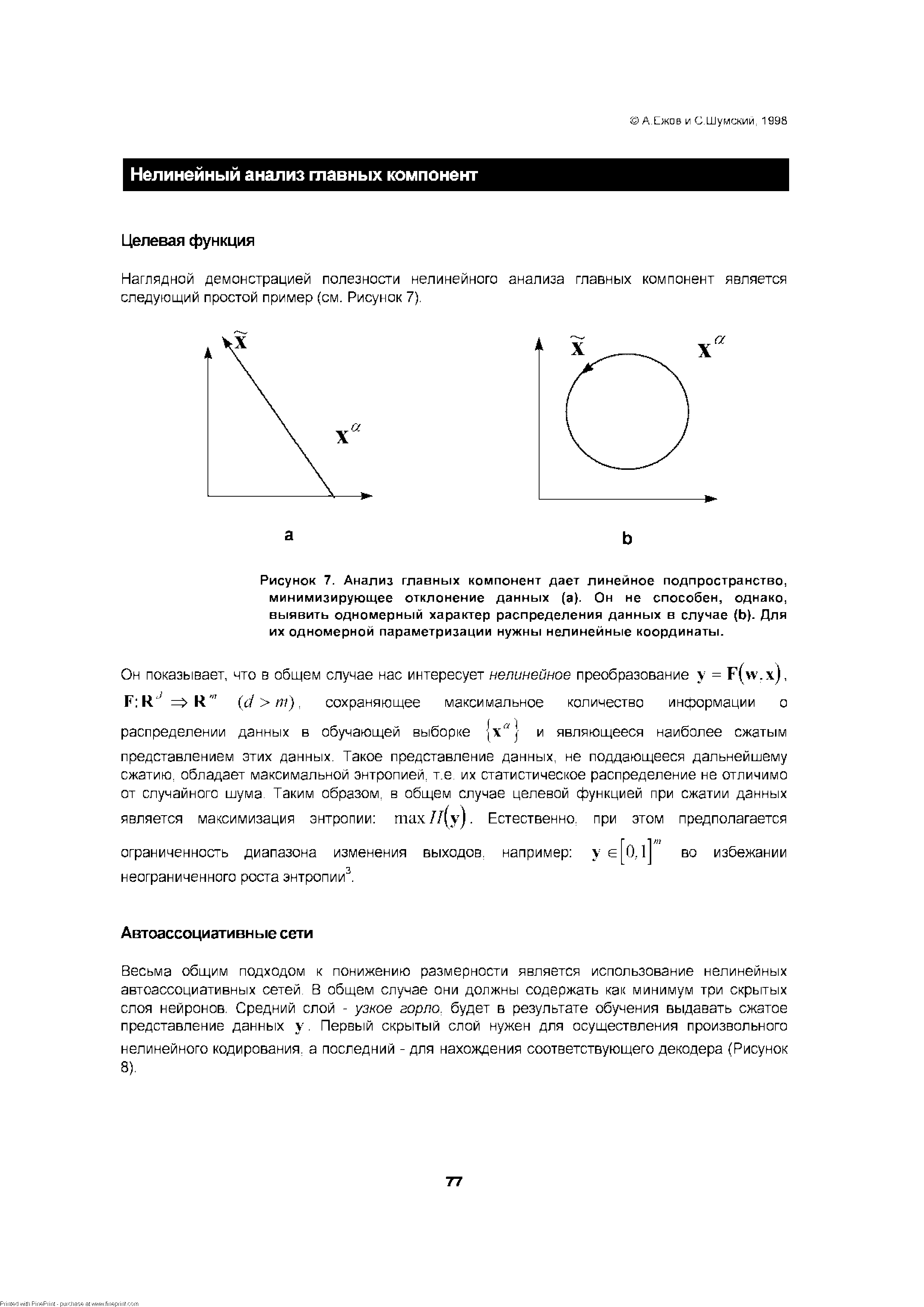 |
Объединяя все т базовых шкал в одно пространство, получаем m-мерное базовое пространство. Таким образом, все пространство параметров К" отображается на пространство субъективных критериев той же размерности. При этом пространство субъективных критериев разбивается лингвистическими переменными на линейные подпространства. Каждая точка базового пространства определяется двумя связанными между собой векторами координат координатами пространства параметров и координатами пространства критериев. Они связаны между собой через базовые шкалы. [c.99]
Однако для разных лингвистических переменных (в разных линейных подпространствах) веса критериев могут меняться с уче- [c.101]
Цифры в линейных подпространствах табл. 7.3 и 7.4 показывают значения функции предпочтения в каждом подпространстве, цифры, отчеркнутые в правом верхнем углу - ранжировку подпространств. С точки зрения руководителя лучшим на табл. 7.3 оказалась решение 2, хотя оно дает плохую очистку, но самоё дешевое. [c.241]
Доказательство. Решение задачи вида (3.6) удовлетворяет соотношению т] — [ — min r - — Д , где минимум берется по всем Д = — , eQ. Совокупность таких разностей Д образует линейное подпространство, которое, в частности, вместе с элементом Д содержит и ЯД, где Л — действительное число. [c.308]
В общем случае при постановке задачи о сглаживании и прогнозе случайных процессов исключение систематических ошибок экстраполяции (равенство нулю первого момента ошибок упреждения) не является обязательным и тем более единственным требованием рациональной фильтрации или рационального прогнозирования. Больше того, в ряде случаев целесообразно расширить область определения задачи и заменить требование о нулевых систематических ошибках ограничениями на их величину. Могут быть указаны и другие неравенства и логические соотношения, которым в тех или иных содержательных задачах фильтрации и прогноза должны удовлетворять, сглаженные или упрежденные точки. Например, может быть ограничена дисперсия или корреляционные моменты случайных величин, зависящих от г (/о + п) и (М- Можно указать содержательные постановки, в которых область определения задачи естественно задавать вероятностными или жесткими ограничениями. Таким образом, в общем случае ограничения задачи сглаживания и экстраполяции высекают в Я не линейное подпространство и не линейное многообразие, а некоторую выпуклую или невыпуклую область G. [c.309]
Обозначим через Li линейное подпространство гильбертова пространства ЯД определяемое элементами вида [c.318]
По существу, wa (t) есть проекция градиента на линейное подпространство, касательное к многообразию, выделенному условием Рг[и ( ), Т]=0. [c.156]
Определение. Линейным подпространством линейного пространства L называется подмножество К векторов пространства L, замкнутое относительно операций сложения и умножения на число, т. е. из того, что векторы а, Ъ е К, следует, что а + Ъ и аа принадлежат К. [c.486]
Пример. Рассмотрим множество векторов из Rn, состоящее из таких векторов, у которых последние п — k координат равны 0. Нетрудно проверить, что это множество является линейным подпространством пространства Д", совпадающим с Rk. [c.486]
Если линейное подпространство К векторного пространства L не совпадает с ним, то его часто называют гиперплоскостью. [c.486]
Образом оператора A L —> М называется множество 1т(.Д), состоящее из всех векторов А(х), х L. 1т(А) является линейным подпространством пространства М. [c.487]
Ядром оператора A L — М называется множество Кет(А), состоящее из всех векторов х е L, таких, что Л(х) — 0. Кег(.А) является линейным подпространством пространства L. [c.488]
Определение. Рангом по строкам матрицы А называется размерность линейного подпространства в Rn, порожденного т векторами-строками матрицы А. [c.494]
Определение. Рангом по столбцам матрицы А называется размерность линейного подпространства в Rm, порожденного п векторами-столбцами матрицы А. [c.494]
Если n-мерный набор данных можно представить как n-мерное пространство, то двумерное пространство (т.е. плоскость) или одномерное пространство (т.е. прямая) будут представлять собой его подпространства. Множество данных может быть представлено в виде подмножества векторов, которые образуют линейное подпространство меньшей размерности. Каждый вектор т-мерного линейного подпространства (где m меньше п) есть линейная комбинация m независимых базисных векторов. Анализ главных компонент является одним из методов изображения векторов данных большой размерности в виде линейной проекции на подпространство меньшей размерности. [c.23]
В линейном программировании область допустимых решений допустимый многогранник) всегда выпукла и всегда находится в неотрицательном подпространстве многомерного (п-мерного) пространства решений. [c.231]
Одним из способов снятия неопределенности в соответствии с поставленной целью является оценка весов критериев. Этому вопросу посвящено довольно много работ. В качестве примера рассмотрим характер снятия неопределенности тремя методами оценки весов критериев теории графов, подпространств текущего состояния и цели, и линейного программирования. [c.105]
Соотношение (3.8) имеет простую геометрическую интерпретацию. Пусть Q — линейное пространство всех элементов A —t, — , eQ. Соотношение (3.8) — равенство нулю скалярного произведения элементов т] — и Д = — при всех A Q — означает, что случайные величины т] — и А некоррелированы. Разность ц — ортогональна к подпространству Q. Точка называется проекцией величины т) на линейное многообразие Q, а разность т — — перпендикуляром к Q из точки г. [c.309]
Доказательство. Рассмотрим гильбертово пространство Нт случайных m-мерных векторов = S", С], а — 1. .... т. Обозначим через L подпространство Нт, порожденное линейными комбинациями значений случайных величин "( ) при ta — 7
Подпространства векторного пространства. Неравенство для размерности подпространства. Теорема о подпространстве полной размерности. Линейная оболочка системы векторов, ее размерность и свойства минимальности. Сумма и пересечение подпространств. Формула для размерности суммы двух подпространств. Дополнительные подпространства, разложение пространства в прямую сумму подпространств. Признаки прямой суммы. Существование алгебраического дополнения к любому подпространству. [c.10]
Размерность подпространства решений однородной системы линейных уравнений. Аффинные многообразия. Линейные задачи аналитической геометрии, метод неопределенных коэффициентов. Прямая, плоскость, гиперплоскость. [c.11]
Анализ главных компонент и факторный анализ являются стандартными методами получения линейных проекций данных на подпространство гораздо меньшей размерности, в котором форма дисперсии исходных данных сохраняется в максимальной степени. В действительности широко используемый критерий собственного значения есть не что иное, как мера дисперсии, объяснимая в рамках предложенной модели. Подобно линейному моделированию, факторный анализ налагает строгие ограничения на используемые данные и наряду с другими обсуждаемыми методами имеет несколько серьезных ограничений в отношении визуализации структуры нелинейных данных. [c.203]
В тех случаях, когда предполагается, что Kt = onst, т.е. зависит от лингвистических переменных каждого критерия, веса линейных подпространств базового пространства могут быть вычислены заранее и ранжированы. В этом случае точка в пространстве критериев J "1, характеризующая данное решение, определяется ее параметрами и принадлежностью к определенному подпространству. Поскольку подпространство ранжировано, то ранжированы и попавшие в них точки. Таким образом, пространство параметров и пространство критериев оказались связанными (отраженными друг в друге). [c.102]
В табл. 7.3 проставлены веса каждого линейного подпространства. Расчет ведется по упрощенной формуле (7.8), когда каждая Kt - onst. Заметим, что балльная оценка расходов в нашем примере должна быть инверсной очень большие - ,h большие - , [c.239]
Множество Q вида (3.7) состоят из точек t(ito) С фиксированным математическим ожиданием, равным Л1т](/о-Нп)- В задаче (3.6) — (3.7) множество Q представляет собой линейное подпространство. В этом случае соотношение (3.8) может быть переписано в виде [c.309]
Паллиативы (метод проекции градиента в общем случае). Выше было показано, что проектирование градиента осуществляется достаточно просто (правда, в линеаризованной постановке, приводящей к проектированию на линейное подпространство) в двух случаях либо при отсутствии дополнительных условий (F(=ff), либо при отсутствии геометрического ограничения на значения и (t) (u( U). Однако большая часть прикладных задач оптимального управления содержит оба сорта условий, а в этом случае проектирование выполняется решением задачи квадратического программирования. К сожалению, идеи и алгоритмы, относящиеся к линейному и нелинейному программированию, мало известны среди специалистов по прикладной механике, которые особенно часто сталкиваются с необходимостью решения задач оптимального управления достаточно общего вида. Именно в этой среде были созданы многочисленные приемы, имеющие целью сформулировать общую задачу как задачу классического типа, либо как простейшую неклассическую задачу. Мы рассмотрим наиболее типичные из этих приемов. Их следует отнести к разряду паллиативов, так как они не снимают трудностей численного решения, а лишь отодвигают их, так сказать, в глубь проблемы. Создание алгоритма приближенного решения задачи оптимального управления можно условно разбить на два этапа [c.160]
Допустимые вариации (1.9), очевидно, образуют линейное подпространство. Возьмем условие непротекания (1.6) сплошной среды через поверхность 2. Для точек, лежащих на Z, (/( ( а, 0) = 0). возможные смещения 8х направлены в сторону, занятую средой [c.12]
Любое подмножество данного линейного пространства, которое само обладает свойствами линейного пространства, называется линейным подпространством. Множество Я, получаемое сдвигом некоторого линейного подпространства L .Rn на вектор aeRn H = L + a, называется аффинным множеством (пространством). Если фундаментальным свойством любого линейного пространства или подпространства является принадлежность ему нулевого вектора, то для аффинного множества это не всегда так. На плоскости примером подпространства является прямая, проходящая через начало координат, а аффинного множества — любая прямая на плоскости. Характеристическим свойством аффинного множества является принадлежность ему любой прямой, соединяющей две любые его точки. Размерность аффинного множества совпадает с размерностью того линейного подпространства, сдвигом которого оно получено. [c.22]
Определение. Множество всех линейных комбинаций векторов oi,..., а е L a ai + aiQ-i + + а а , оц е R называется пространством, пороэ/сдеиным векторами ai,...,a . (Проверьте, что оно является линейным подпространством векторного пространства L.) [c.486]
Линейная независимость, 485 Линейное подпространство, 486 Линейный оператор, 487 Лямбда Хекмана, 344 [c.571]
Д 0каза телЦь с т в о. Заметим, что поскольку ф" ( ),/= 1,..., г, определяющие первые моменты С (t), предполагаются линейно независимыми, то для каждого а, а = 1,..., т, найдутся такие точки t , . .., t G G [4— Т, ta], что 11
На практике полная коллинеарность встречается исключительно редко. Гораздо чаще приходится сталкиваться с ситуацией, когда матрица X имеет полный ранг, но между регрес-сорами имеется высокая степень корреляции, т. е. когда матрица Х Х, говоря нестрого, близка к вырожденной. Тогда говорят о наличии мультиколлинеарности. В этом случае МНК-оценка формально существует, но обладает плохими свойствами. Это нетрудно объяснить, используя геометрическую интерпретацию метода наименьших квадратов. Как уже отмечалось, регрессию можно рассматривать как проекцию в пространстве Rn вектора у на подпространство, порожденное столбцами матрицы X. Если между этими векторами существует приблизительная линейная зависимость, то операция проектирования становится неустойчивой небольшое изменение в исходных данных может привести к существенному изменению оценок. Рисунок 4.1 наглядно это демонстрирует. Векторы у к у мало отличаются друг от друга, но в [c.110]
Линейная оболочка юсегда является подпространством. Если подпространствоF содержит точки М Мг,. .., Mk, то оно содержит и всю линейную оболочку этих точек. [c.87]
