Условным математическим ожиданием оператора А относительно подпространства L называется оператор PLA. Это условное математическое ожидание обладает свойствами обычного математического ожидания 1. PLA = А, если A L - измерим [c.15]
Семейство подпространств Ht, t называется потоком, если г Операторная [c.15]
| Рисунок 7. Анализ главных компонент дает линейное подпространство, минимизирующее отклонение данных (а). Он не способен, однако, выявить одномерный характер распределения данных в случае (Ь). Для их одномерной параметризации нужны нелинейные координаты. | 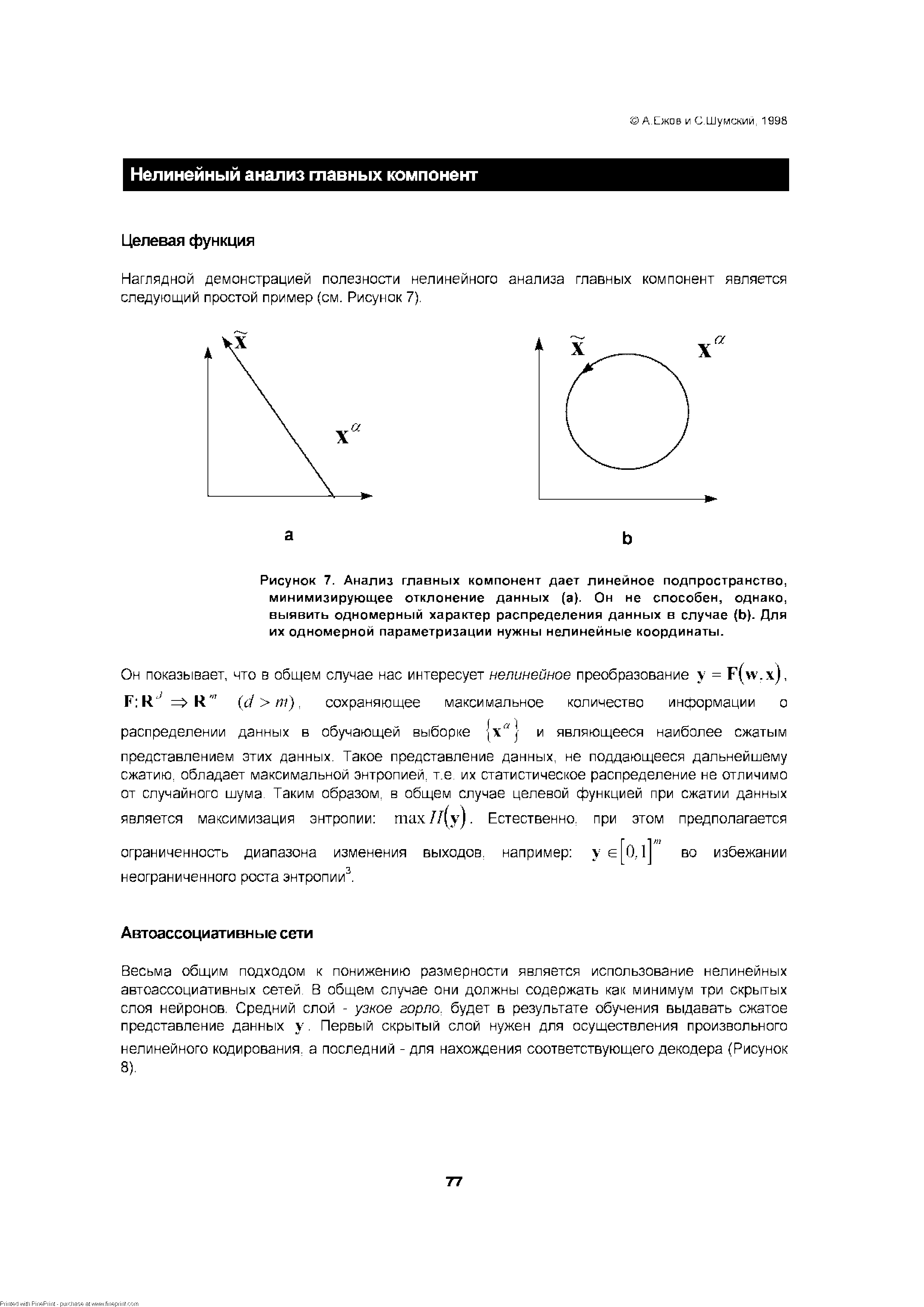 |
Т. о. два непересекающихся подпространства 7й" и Т образуют полное [c.5]
Изменяя границы базового подпространства будем изменять степень [c.10]
Выбор оптимального подпространства Б на основе информационного [c.13]
Применительно к задаче управления качеством, подпространство Y+ [c.34]
Размерность конуса совпадает с размерностью минимального подпространства, содержащего данный конус. [c.123]
| Таблица 2.2. Когнитивное подпространство потребителя и факторы потребностей |  |
В линейном программировании область допустимых решений допустимый многогранник) всегда выпукла и всегда находится в неотрицательном подпространстве многомерного (п-мерного) пространства решений. [c.231]
Объединяя все т базовых шкал в одно пространство, получаем m-мерное базовое пространство. Таким образом, все пространство параметров К" отображается на пространство субъективных критериев той же размерности. При этом пространство субъективных критериев разбивается лингвистическими переменными на линейные подпространства. Каждая точка базового пространства определяется двумя связанными между собой векторами координат координатами пространства параметров и координатами пространства критериев. Они связаны между собой через базовые шкалы. [c.99]
Однако для разных лингвистических переменных (в разных линейных подпространствах) веса критериев могут меняться с уче- [c.101]
Одним из способов снятия неопределенности в соответствии с поставленной целью является оценка весов критериев. Этому вопросу посвящено довольно много работ. В качестве примера рассмотрим характер снятия неопределенности тремя методами оценки весов критериев теории графов, подпространств текущего состояния и цели, и линейного программирования. [c.105]
На основе критериального анализа ситуации, опыта и знаний. В рамках этого способа оцениваются веса (величины значимости) критериев, например на основе использования подпространств текущего состояния и цели, которая рассмотрена ранее в разделе 3.4, Не будем повторять описание процедуры оценки. Напомним только, что при этом подходе значимость, важность У-го критерия (его "вес") - [c.230]
На основе критериального анализа ситуации, прогнозирования динамики, опыта и знаний. Введем еще одно подпространство H(t) в том же критериальном пространстве Яда. Это подпространство, к которому могут принадлежать значения критериев, характеризую- [c.230]
Цифры в линейных подпространствах табл. 7.3 и 7.4 показывают значения функции предпочтения в каждом подпространстве, цифры, отчеркнутые в правом верхнем углу - ранжировку подпространств. С точки зрения руководителя лучшим на табл. 7.3 оказалась решение 2, хотя оно дает плохую очистку, но самоё дешевое. [c.241]
Теперь в нашем иллюстративном примере вернемся к множествам S и D и покажем как выбор множества S (в котором желательно иметь значения критериев) влияет на решение руководителя. Если руководитель считает, что загрязненность воды не имеет большого значения, лишь бы затраты были небольшие, он может определить область S как подпространства 7 и 12 табл. 7.3, считая решение 2 наилучшим. Текущее состояние на табл. 7.3 обозначено тек . Руководитель может предложить сократить расходы по очистке и вода из "очень загрязненной" станет "чрезвычайно загрязненной". [c.242]
Если руководитель считает чрезвычайно важной чистоту воды и готов для ее очистки нести расходы, он может выбрать в качестве области S, например, подпространства 9 и 14 табл. 7.4, и, если координаты текущей точки те же, что и на табл. 7.3, то не пожалеть расходов на перевод ее в подпространство 14 табл. 7.4. В подпространство 9 она уже попасть не может, т.к. при средних расходах улучшить очистку воды, видимо, нельзя. [c.242]
Наконец, о подпространствах в левом верхнем углу табл. 7.3 и 7.4. Это идеальные подпространства, но они практически не достижимы. Нельзя бесплатно или почти бесплатно получать чистую воду в загрязненном районе. Столбец нет затрат из табл. 7.3 и 7.4 фактически следовало бы убрать. [c.242]
Для прогнозирования динамики развития событий может быть введено еще одно подпространство H(t) в том же критериальном пространстве Л"1. Это подпространство, к которому могут принадлежать значения критериев, характеризующих объект по оценкам руководителя через время t, если на объект не подавать управляющих воздействий. Например, оценку экономики по критерию уровня инфляции ЛПР характеризует следующим образом в настоящий момент - удовлетворительно, желательное состояние - хорошее, через время t (например, 6 мес.), если не подавать управляющих воздействий она окажется в плохом состоянии. Таким образом, несмотря на относительное благополучие в настоящий момент, необходимо принимать энергичные меры. [c.488]
В задаче (9.3) играет роль только проекция вектора z на подпространство, натянутое на векторы Vfi(X°). Поэтому вдоль направления наискорейшего спуска [c.124]
Будем обозначать через Я 1 гильбертово пространство случайных т-мерных векторов с нулевым математическим ожиданием и ограниченной дисперсией. Выделим в Ят подпространство L (/ , Т), элементы кото- [c.304]
Введем в рассмотрение подпространство Z.mft, Т) пространства Я Подпространство L (tQ, Т) порождено случайной вектор-функцией [c.306]
Можно показать, что, если х0 и У0 - множества решений задач (4.64) и (4.66) и ха n int R Ф О, где int R - внутренность множества R, то х образовано пересечением заданного афинного подпространства Ь пространства Ет и ортанта Г"1. Афинное подпространство La определяется из условия [c.133]
Пусть К - коммутативное -кольцо самосопряженных операторов сепарабельного гильбертова пространства Н замкнутое относительно слабой сходимости. В дальнейшем будем полагать, что все упбмянутые ниже операторы принадлежат кольцу К. Если речь идет о некотором подпространстве L, будем предполагать, что оператор проектирования на это подпространство PL принадлежит К. [c.15]
Несмотря на то что компонент информационного ресурса в принципе может позиционироваться в любой точке восьмимерного пространства, задаваемого указанной выше системой координат, практический интерес представляют несколько подпространств. [c.273]
Прежде всего само векторное пространство — это выпуклый К. Все его подпространства, образованные путем деления пространства на две части разделенные гиперплоскостями, проходящими через начало координат, — также выпуклые конусы. Возьмем, напр., множество векторов со всеми положительными координатами. Такой К. называется первым ортантом (по аналогии с первым квадрантом, множеством точек на плоскости, имеющих положительные координаты). [c.153]
ПОДПРОСТРАНСТВО [subspa e] — такое подмножество данного пространства R, которое само является пространством того же типа, что и R. [c.266]
В тех случаях, когда предполагается, что Kt = onst, т.е. зависит от лингвистических переменных каждого критерия, веса линейных подпространств базового пространства могут быть вычислены заранее и ранжированы. В этом случае точка в пространстве критериев J "1, характеризующая данное решение, определяется ее параметрами и принадлежностью к определенному подпространству. Поскольку подпространство ранжировано, то ранжированы и попавшие в них точки. Таким образом, пространство параметров и пространство критериев оказались связанными (отраженными друг в друге). [c.102]
Оценка весов критериев с использованием подпространств текущего состояния и дели Для критериального анализа ситуации введем в рассмотрение в пространстве критериев два подпространства S и D. Как и пространство критериев, подпространства S и D являются подмножествами m-мерного Евклидового пространства (т - число критериев) SG К", Deft S - это подпространство, в котором руководителю желательно иметь значения критериев, характеризующие объект после выполнения решения (сценария, выполнения управляющего воздействия). В тех случаях, когда желательное состояние задается координатами, а не интервалами, подмножество S может состоять из одной точки -% D - это подмножество точек определяющее по оценкам руководителя текущее состояние объекта, относительно которого принимается решение. Множество D может состоять из одной точки, обозначим ее d если текущее состояние задается координатами, а не интервалами, [c.107]
В табл. 7.3 проставлены веса каждого линейного подпространства. Расчет ведется по упрощенной формуле (7.8), когда каждая Kt - onst. Заметим, что балльная оценка расходов в нашем примере должна быть инверсной очень большие - ,h большие - , [c.239]
Также как в предыдущих разделах этой главы для ранжирования и выбора критериев, применяется методика преложенная в [Ц.5, 12.6] (см. также раздел 7.2), основанная на том, что для критериального анализа ситуации вводится в рассмотрение в пространстве критериев два подпространства S и D. Как и пространство критериев, подпространства S и D являются подмножествами ти-мерного Евкли-дового подпространства (т - число критериев) Se R , Detf". S - это [c.486]
Смотреть страницы где упоминается термин Подпространство
: [c.185] [c.76] [c.80] [c.6] [c.7] [c.7] [c.7] [c.9] [c.10] [c.11] [c.11] [c.34] [c.53] [c.481] [c.487]Справочник по математике для экономистов (1987) -- [ c.86 ]
