Наиболее характерной особенностью многих процессов биологического уровня являются процессы обмена вещества и энергии. Построение моделей этих процессов основывается на соответствующих законах сохранения (например, при описании трофических связей — кто кого ест) и функциях поведения. Вместе они позволяют дать замкнутое математическое описание исследуемого процесса. Таким образом, в окончательной форме математическая модель популяции, например, не содержит описания информационных процессов. Они остаются как бы за кадром, функции поведения являются, по существу, их параметризацией, т. е. приближенным представлением сложных процессов относительно простой функциональной зависимостью. [c.9]
Можно выделить шесть основных этапов эконометрического моделирования постановочный, априорный, этап параметризации, информационный, этапы идентификации и верификации модели [1]. [c.21]
Практическое применение экономико-математических методов в планировании нефтеперерабатывающих производств требует создания специального программного обеспечения, реализующего алгоритмы параметризации, моделирования, оптимизации НПП и анализа решений. Автоматизация процессов построения модели и интерпретации результатов решений требует, как правило, разработки оригинальных программных средств, учитывающих структурные, функциональные и информацион- [c.178]
Блок 15— Параметризация модели". Осуществляется пересчет статистических характеристик модели и их обновление на МД в блоке 16. [c.184]
| Рисунок 7. Анализ главных компонент дает линейное подпространство, минимизирующее отклонение данных (а). Он не способен, однако, выявить одномерный характер распределения данных в случае (Ь). Для их одномерной параметризации нужны нелинейные координаты. | 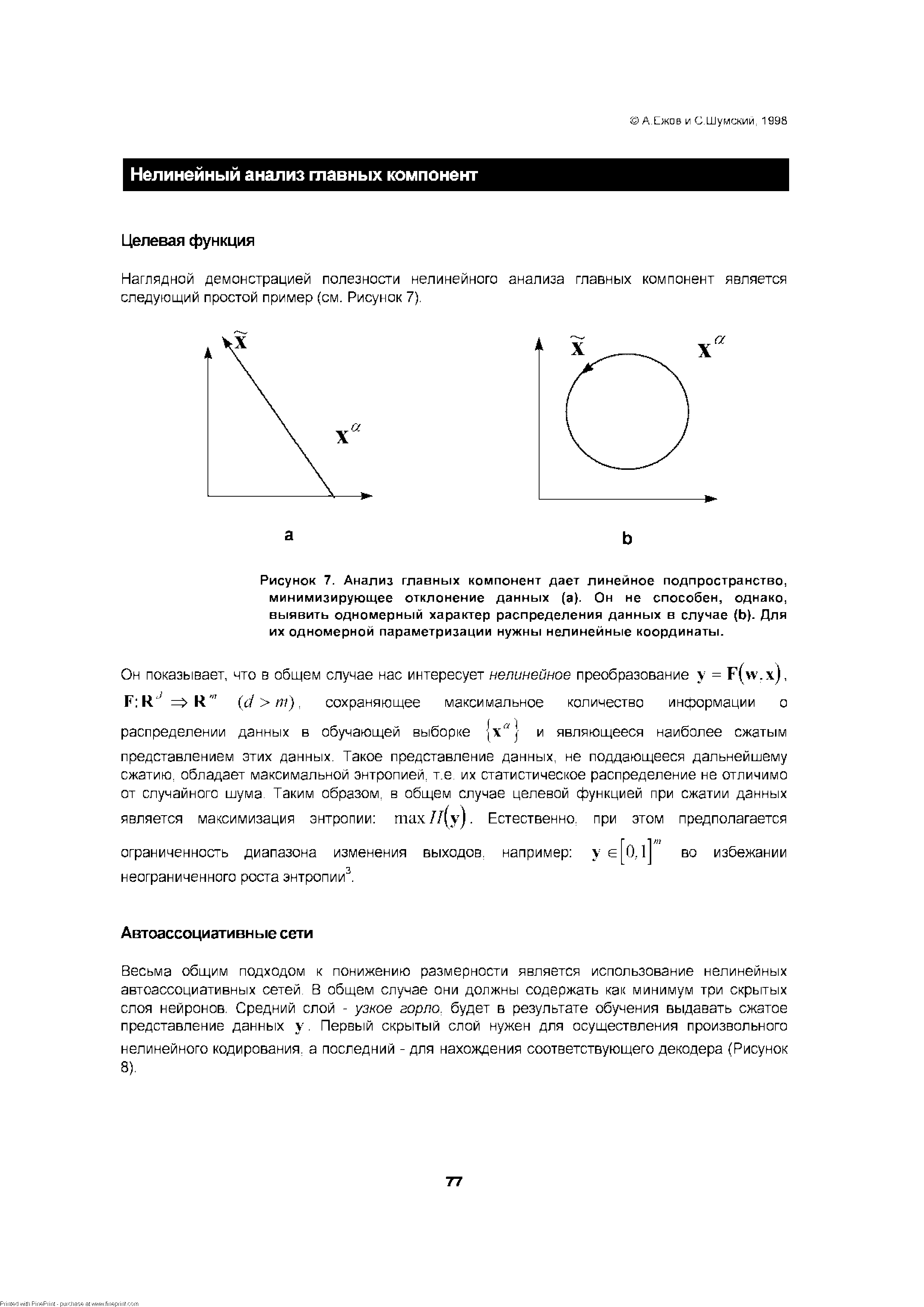 |
Монотонная кривая относится к следующей параметризации по степенному закону [c.229]
В международной функциональной стандартизации ИТ принята жесткая трактовка понятия профиля. Считается, что основой профиля могут быть только международные и национальные утвержденные стандарты (не допускается использование стандартов де-факто и нормативных документов фирм). Подобное понятие профиля активно используется в гамме международных функциональных стандартов, конкретизирующих и регламентирующих основные процессы и объекты взаимосвязи открытых систем, в которых возможна и целесообразна жесткая формализация профилей (функциональные стандарты ИСО 10607 — ИСО 10613 и соответствующие им ГОСТы Р). Однако при таком подходе невозможны унификация, регламентирование и параметризация множества конкретных функций и характеристик сложных объектов архитектуры и структуры современных ИС. [c.65]
В данной главе выделены совокупность функциональных профилей ИС и набор профилей, обеспечивающих технологическую поддержку и необходимое качество при создании функциональных компонентов ИС. Предложена дальнейшая структуризация и выделение профилей применительно к конкретным объектам и процессам. Каждый из выделенных профилей для последующего длительного использования проходит стадию формирования, адаптации и параметризации применительно к характеристикам стандартизируемых объектов или процессов создания ИС. Такая подготовка профилей должна проводиться с учетом применяемых методов и средств, текущего состояния и ведущихся работ на реальных компонентах ИС. Подготовка профилей к применению также должна учитывать и реальное состояние проекта ИС. При этом возможны следующие варианты [c.71]
Рассмотренные выше общие методические положения создания и применения комплекса профилей ИС следует детализировать для каждого профиля до уровня Руководящих указаний по адаптации и параметризации и Методик по применению для конкретных проблемно-ориентированных областей или конкретных проектов ИС. В этих документах должны быть представлены конкретные операции, структура и содержание документов, обеспечивающих регламентированное применение профиля и контроль соответствия процессов и объектов ИС требованиям и рекомендациям профиля. Положения каждой методики и сценарии их конкретного применения необходимо поддержать технологией и средствами автоматизации их реализации, документирования и контроля соответствия утвержденному профилю. Для создания руководящих указаний и методик применения профилей при подготовке к проектированию ИС следует утвердить их номенклатуру и требования к содержанию. Дальнейшие работы организовывают для создания конкретных методик применения каждого профиля в тесном взаимодействии с подразделениями, которым предстоит использовать соответствующие профили. Такие методики должны предусматривать длительное развитие, расширение и модернизацию функций компонентов и ИС в целом. С этой целью организуют учебные курсы для специалистов по применению и контролю соблюдения положений каждого профиля. [c.84]
См. также Активный (условный) статистический прогноз, "Барометры ", Вариантные прогнозы, Горизонт прогнозирования, Демографический прогноз, Диапазон осуществимости прогноза, Долгосрочное прогнозирование, Зона неопределенности, Интервальный прогноз, Комплексное прогнозирование, Морфологический анализ, Научно-технический комплексный прогноз, Нормативный прогноз, Ошибки в прогнозировании, Параметризация процесса, Пассивный (безусловный) статистический прогноз, Поисковый прогноз, Порог, Прогноз, Прогнозирование спроса, Ретроспективный прогноз, Сценарий, Целевой прогноз. [c.283]
В данной работе гидрологические характеристики находятся на основе решения уравнений теории мелкой воды [Воль-цингер и др., 1977] с параметризацией влияния силы трения о дно и учетом турбулентного обмена по горизонтали [c.99]
На первом этапе, учитывая простейшую параметризацию управлений и создание ортогональной сети на основе определений УКУ, формируют сеть приближенных решений. [c.68]
Если в условиях теоремы 7 положить тг = ve П и г/ = (Ф), то информационная матрица в терминах параметризации (а, тг, г/ ) будет равна [c.431]
Параметризация компонентов СМОД. Основное назначение операций параметризации — обеспечить возможность количественного и качественного сопоставления различных вариантов компонентов проектируемой системы обработки. Кроме того, благодаря параметризации улучшается формирование инструментальных универсумов. [c.31]
Применение технологических операций по параметризации компонентов СМОД обеспечивает простоту привязки ТПР к конкретным условиям объекта управления, повышает уровень их адаптивности. [c.122]
Параметризация компонентов СМОД 31 [c.244]
Ограничимся этими общими замечаниями более точное представление о том, что имеется в виду, дают примеры, где эту программу удалось реализовать и получить весьма точные решения сложных вариационных задач. Стоит отметить, что качественный анализ задачи, позволяющий построить необходимую параметризацию семейства решений П-системы, может быть основан как на аналитической работе, так и на изучении приближенных решений задачи, полученных каким-либо численным методом, эффективным, хотя и дающим относительно грубое решение. [c.119]
Если всерьез полагать, что формула (11) характеризует эффективность процесса поиска решения, то следовало бы еще больше повысить ее, заменив (10), например, уравнением х— — 10е X X/ 1/, т. е. V [х (s)] = F0e l0 -s. Ясно, что эффективность поиска связана не с характером параметризации траектории (12), а с затратами реального машинного времени, т. е. с числом вычислений функций / (х), fx (х), затрачиваемых на достижение достаточно малых значений II/ (ж) II. С практической точки зрения теорема 2 гарантирует успех процесса поиска с достаточно малым шагом s в этом случае процесс типа [c.385]
Этап 4 (определение класса допустимых решений). Главной целью исследователя на этом этапе является определение общего вида, структуры искомой связи между Y и X, или, другими словами, описание класса функций F, в рамках которого он будет производить дальнейший поиск конкретного вида интересующей его зависимости (см. задачи а) и 3 в В.1). Чаще всего это описание дается в форме некоторого параметрического семейства функций / (X в), поэтому и этап этот называют также этапом параметризации модели. Так, определив в примере В.1, что поиск зависимости среднедушевых семейных сбережений //ср от величины их среднедушевого дохода х мы будем производить в классе F = (60 + QI линейных функций, мы тем самым завершили четвертый этап исследования (но конкретных числовых значений параметров 00 и 0 мы к этому моменту еще не знаем). [c.49]
Ограничимся рассмотрением таблиц с двусторонней группировкой. Для них сформулированы основные гипотезы и указаны методы их проверки, описана логарифмически-линейная параметризация, приведены различные меры зависимости между строками и столбцами таблицы. Вводятся понятия энтропии случайной величины и информации, содержащейся в одной случайной величине относительно другой случайной величины, представляющие самостоятельный интерес. [c.125]
Логарифмически-линейная, параметризация таблиц со- [c.127]
Для описания совместного распределения хц предложена логарифмически-линейная параметризация таблиц сопряженности, в которой предполагается, что [c.142]
Следует подчеркнуть, что этап 4 (см. В.6), т. е. этап исследования, посвященный выбору общего вида функции регрессии (параметризация модели), бесспорно, является ключевым от того, насколько удачно он будет реализован, решающим образом зависит точность восстановления неизвестной функции регрессии / (X). В то же время приходится признать, что этот этап находится, пожалуй, в самом невыгодном положении к сожалению, не существует системы стандартных рекомендаций [c.175]
Были подвергнуты расчету и сравнительному анализу три варианта параметризации модели [c.178]
Этап параметризации регрессионной модели, т. е. выбора параметрического семейства функций (класса допустимых решений), в рамках которого производится дальнейший поиск неизвестной функции регрессии, является одновременно наиболее важным и наименее теоретически обоснованным этапом регрессионного анализа. [c.207]
В случае произвольной параметризации с точностью до О (у8) [c.245]
При линейной параметризации ft (9) — 9 f° (X,-) решение [c.304]
Для линейного случая решение достигается за один шаг. При нелинейной параметризации процедура повторяется [c.306]
Для рассматриваемой экстремальной задачи метод Ньютона—Гаусса близок методу Ньютона. При линейной параметризации они совпадают. Их близость при малых вторых производных Ф1з очевидна. Имеется и более глубокая причина их близости. Действительно, при п —> оо и некоторых не слишком ограничительных предположениях в силу закона больших чисел имеем следующую сходимость (с вероятностью единица) [c.306]
При линейной параметризации метод Ньютона—Гаусса без подсчета производных дает точное решение задачи мнк на первой итерации, если pt = 1. [c.311]
При квадратичной функции J (в) (в нашем случае — линейной параметризации) после т шагов матрица Н, подсчитываемая любым из методов а)—в), в точности совпадает с матрицей Hs, определенной в п. 9.3. Иными словами, при ps = 1 в этом случае точное решение исходной экстремальной задачи будет заведомо получено за т шагов. Если ps выбирается из [c.313]
ОЦЕНКА ПАРАМЕТРОВ МОДЕЛИ (ЕЕ ПАРАМЕТРИЗАЦИЯ) [parameter estimation] — 1. Этап построения экономико-математической модели (напр., эконометрической модели) заключается в определении численных значений существенных параметров модели, выявленных на предварительных этапах анализа исследуемого объекта или процесса (см. Идентификация объекта, Спецификация модели). Параметры модели численно оцениваются по данным, полученным путем экономического эксперимента и статистического наблюдения — чаще всего методом наименьших квадратов, методом максимального правдоподобия, а также некоторыми другими статистическими методами. На этой основе можно производить различные операции над моделью (напр., строить прогнозы поведения системы). [c.254]
ПАРАМЕТРИЗАЦИЯ [parametrization] — элемент системного анализа объекта (процесса), который заключается в выделении существенных воздействующих факторов (см. Идентификация системы), их описании и количественной оценке полученных параметров связи (см. Оценка параметров модели). П., как правило, не может быть выполнена на основе строго определенных процедур и во многом определяется опытом и интуицией исследователя (т.е. носит эвристический характер). Иногда для создания полноценной модели приходится заменять и уточнять список существенных параметров, а также корректировать их оценки. К тому же по мере развития исследуемого процесса одни параметры могут терять свое значение, другие — наоборот, увеличивать. Так что процесс П. может быть длительным и непрерывным. [c.258]
Параметризация задачи оптимального управления. В ряде случаев задачу оптимального управления удобно решать в два этапа. На первом этапе оптимальное решение находится с точностью до набора неопределенных параметров. После такого решения задача сводится к конечномерной задаче условной оптимизации относительно вектора неопределенных параметров. Введение неопределенных параметров представляет собой реализацию известного из школьной математики принципа не знаем — обозначим , согласно которому неизвестную величину обозначают через х и по условиям задачи составляют уравнение относительно этой неизвестной. В экстремальных задачах неопределенные параметры позволяют провести декомпозицию задачи, т.е. разбиение ее на несколько подзадач, решение каждой из которых зависит от значения параметра, входящего в другие подзадачи. Так было сделано, например, при исследовании тепловых машин с источниками конечной емкости (гл. 4). В ряде случаев введение параметра позволяет найти форму оптимального решения с точностью до неизвестного параметра, как это было сделано в гл. 5 при определении идеальной рабочей линии процесса ректификации. [c.402]
Другой путь борьбы с неединственностью носит более принципиальный характер и, если его удается реализовать, приводит к хорошим практическим результатам. Однако его реализация весьма трудна, требует индивидуального анализа решаемой задачи. Общих рецептов здесь нет. Поэтому мы ограничимся лишь кратким изложением существа дела. Метод состоит в качественном опжсании множества решений П-системы, которое часто допускает однозначную параметризацию, причем число параметров равно числу неиспользованных конечных соотношений в краевой задаче для П-системы. Формально это совпадает с приведенной выше и отвергнутой схемой рассуждений. Но дело в том, что начальные данные задачи Коши не могут быть взяты в качестве этой системы параметров. Нужно искать другие, успех здесь требует тщательного качественного анализа задачи. [c.119]
Распределения с ДСЗ были введены в статистическую практику С. Чоу [174, 175, 176]. Если не считать краткого изложения результатов Чоу в [48], они не нашли еще отражения в монографической литературе. В отечественной литературе разработка теоретических вопросов, примыкающих к этому новому направлению, дана в [40, 61]. На работы В. И. Заруцкого [58, 59] мы существенно опираемся в последующем изложении. 4.1.3. Математические задачи, связанные с изучением распределений с ДСЗ. Прежде всего надо более четко описать класс распределений с ДСЗ и выявить соотношения между различными параметризациями одного и того же распределения, возникающими при разном упорядочении координат. Ведь даже в простейшем случае, когда координаты образуют цепь Маркова, возможны два упорядочения в прямом направлении цепи Маркова и в обратном. Необходимо также найти аналог выявленному на цепях Маркова соотношению, что прямым связям отвечает более высокая корреляция между координатами (см. 4.2). [c.146]
Использование многомерной регрессии для параметризации многомерных распределений. Плотность р (X) распределения р-мерного случайного вектора X = (Х< > Х<2>) = =(х >,. ..,
Вересков А. И., Л е в и н В. Е., Федоров В. В. Ре-гуляризированиый м. н. к. без производных. — В кн. Линейная и нелинейная параметризация в задачах планирования экспериментов. М., 1981, с. 20—27. [c.461]
Смотреть страницы где упоминается термин Параметризация
: [c.22] [c.303] [c.181] [c.480] [c.57] [c.19] [c.96] [c.461] [c.190] [c.231] [c.385]Вводный курс эконометрики (2000) -- [ c.11 , c.97 ]
