Так как второе слагаемое полученного выражения постоянно, то условная оптимизация рассматриваемого вида целевой функции, т. е. (5.41), оказывается эквивалентной условной оптимизации целевой функции вида [c.164]
Если предположить, что существует rD — ограничение сверху на ставку депозитов, то задача поиска безусловного максимума функции T[(rD,rL) трансформируется в задачу условной оптимизации с одним связующим ограничением [c.110]
Подставляя (10) в (6) и учитывая (9), решаем задачу условной оптимизации и [c.51]
Ф(у) — min является стандартной задачей условной оптимизации. [c.81]
В итоге решения данной задачи условной оптимизации полу- [c.67]
Решая задачу условной оптимизации, получаем [c.120]
Использование задачи условной оптимизации (1-3) при управлении [c.12]
Имея в виду, что курс предназначен не для специалистов в области исследования операций, а для менеджеров, а также учитывая всегда неизбежный недостаток времени, автор не включил в настоящий курс традиционные для курсов исследования операций вопросы нелинейного и динамического программирования. Основная причина в том, что не существует универсальных компьютерных алгоритмов решения задач нелинейной и многошаговой оптимизации. Использование имеющихся программ и алгоритмов требует более серьезного внимания к деталям модели и алгоритма, чем возможно уделить в настоящем курсе. Вместе с тем собственно концепция условной оптимизации, которая обязательно должна быть усвоена читателем, достаточно хорошо может быть проиллюстрирована примерами линейного (и цело численного) программирования. [c.19]
В задачах динамического программирования первый пункт учитывают, делая на каждом шаге условные предположения о возможных вариантах окончания предыдущего шага и проводя для каждого из вариантов условную оптимизацию. Выполнение второго пункта обеспечивается тем, что в задачах динамического программирования условная оптимизация проводится от конца процесса к началу. Сперва оптимизируется последний тп-й шаг, на котором не надо учитывать возможные воздействия выбранного управления хт на все последующие шаги, так как эти шаги просто отсутствуют. Делая предположения об условиях окончания (m-l)-ro шага, для каждого из них проводят условную оптимизацию тп-го Шага и определяют условное оптимальное управление хт. Аналогично поступают для (m-l)-ro шага, делая предположения об исходах окончания (т-2)-го шага и определяя условное оптимальное управление на (т-1)-м шаге, приносящее оптимальный выигрыш на двух последних шагах — (тп-1) и т. Так же действуют на всех остальных шагах до первого. На первом шаге, как правило, не надо делать условных предположений, так как состояние системы перед первым шагом обычно известно. [c.271]
Условная оптимизация начинается с последнего 12-го шага. Для i=12 рассматриваются возможные состояния системы t=0..12. Функциональное уравнение на 12-м шаге имеет вид [c.274]
Условная оптимизация 11-го шага [c.275]
Этап условной оптимизации заканчивается после заполнения табл. 4.2.2. [c.278]
Условная оптимизация 242, 372 Условное распределение случайных [c.493]
Таким образом, решение управленческой задачи состоит в условной оптимизации управленческих решений в рамках человеко-машинной интерактивной процедуры. [c.98]
Процесс оптимизации (выработки оптимального решения) можно трактовать как поиск и выбор наилучшего с некоторой точки зрения варианта среди множества допустимых. Оптимизация представляет процесс нахождения экстремума (максимума или минимума) функции при заданных ограничениях (условная оптимизация) или без ограничений (безусловная оптимизация). [c.207]
Для обратимых процессов AS = 0, в остальных случаях AS > > 0. Предельное значение коэффициента эффективности дает решение задачи условной оптимизации [c.213]
| Рис. 9.4. Случай, когда решение х задачи условной оптимизации является стационарной точкой ограничения f(x) = 0 (вырожденный) | 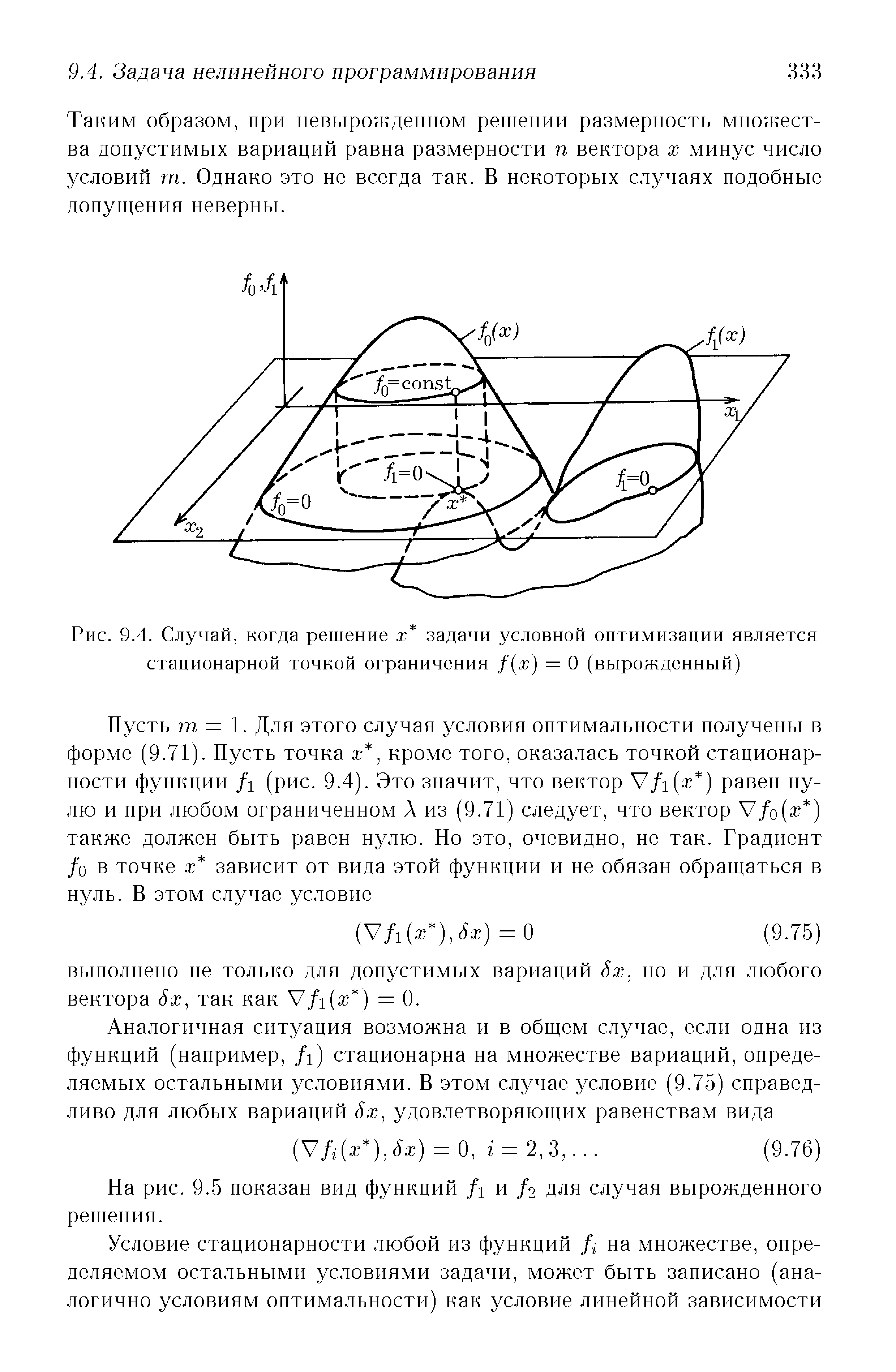 |
Более того, понятие седловых точек является ключевым для теории условной оптимизации при ограничениях типа неравенств. (Примеч. пер.) [c.183]
Найти условия второго порядка задачи условной оптимизации из упр. 12.2. [c.188]
ОПТИМАЛЬНАЯ (ИЛИ ОПТИМИЗАЦИОННАЯ) ЗАДАЧА [optimization problem] — экономико-математическая задача, цель которой состоит в нахождении наилучшего (с точки зрения какого-то критерия) распределения наличныхресурсов. (Иногда то же Экстремальная задача.) Решается с помощью оптимальной модели методами математического программирования, т.е. путем поиска максимума или минимума некоторых функций или функционалов при заданных ограничениях (условная оптимизация) и без ограничений (безусловная оптимизация). [c.242]
Здесь уа — концентрация отделяемого компонента в очищаемом газе. Предельная производительность АДЦ. Под производительностью АДЦ будем понимать количество компонента, отобранного из раствора за время его пребывания в десорбере. Задача сводится к усредненной задаче условной оптимизации вида [c.204]
Вместе с тем невыпуклость / (С) часто не препятствует использованию квадратичного штрафа. Пусть, например, / (С) = 1 + С2 (рис. 9.13, б), функция вогнута и использование расширения Лагран-жа не позволяет свести задачу условной оптимизации к безусловной. Функция достижимости в задаче с использованием квадратичного штрафа имеет вид [c.353]
Параметризация задачи оптимального управления. В ряде случаев задачу оптимального управления удобно решать в два этапа. На первом этапе оптимальное решение находится с точностью до набора неопределенных параметров. После такого решения задача сводится к конечномерной задаче условной оптимизации относительно вектора неопределенных параметров. Введение неопределенных параметров представляет собой реализацию известного из школьной математики принципа не знаем — обозначим , согласно которому неизвестную величину обозначают через х и по условиям задачи составляют уравнение относительно этой неизвестной. В экстремальных задачах неопределенные параметры позволяют провести декомпозицию задачи, т.е. разбиение ее на несколько подзадач, решение каждой из которых зависит от значения параметра, входящего в другие подзадачи. Так было сделано, например, при исследовании тепловых машин с источниками конечной емкости (гл. 4). В ряде случаев введение параметра позволяет найти форму оптимального решения с точностью до неизвестного параметра, как это было сделано в гл. 5 при определении идеальной рабочей линии процесса ректификации. [c.402]
Условия, при которых классические процедуры стохастической аппроксимации сходятся к искомому экстремуму, требуют выпуклости или по крайней мере одноэкстремальности функции -Мш (со, х) по х. Это значит, что для использования стохастической аппроксимации в качестве итеративного метода решения задач стохастического программирования необходимо модифицировать классические схемы применительно к задачам условной оптимизации и отказаться от требования выпуклости или одноэкстремальности Мщ<р (ш, х). [c.343]
