Безусловный максимум функции 30 [c.460]
Классические методы безусловной оптимизации. Начнем с самой простой задачи — задачи безусловной оптимизации. Эта задача состоит в выборе такого вектора х Еп, на котором достигается максимум функции U(x), заданной на всех х Еп. Особенности описываемых методов продемонстрируем в одномерном случае, когда х — скаляр. [c.43]
Если предположить, что функция Tl(rD,rL) является вогнутой, то необходимое и достаточное условие для точки ее безусловного максимума (/-д, r L) задается уравнениями [c.110]
Это - безусловный максимум целевой функции если мы возь- [c.43]
Отметим, что если в задаче НП требовалось бы найти не максимум, а минимум /о (а ) на том же множестве допустимых решений, то условия (9.72), (9.73), определяющие х и Л, не изменились бы, так как при выводе необходимых условий минимума в неравенствах (9.69) фигурировал бы знак >, однако для внутренней точки D такое неравенство переписывается как равенство, т.е. принимает вид (9.70), что и приводит к условиям (9.72). Это не удивительно потому, что для задачи о безусловном максимуме и минимуме дифференцируемой функции необходимые условия оптимальности совпадают. [c.332]
Рассмотрим случай, когда безусловный максимум целевой функции оказывается на множестве D. В терминах функции достижимости этот факт выразится в том, что функция /Q (С) имеет абсолютный максимум на множестве УС в точке С — 0. Действительно, абсолютный максимум функции /о (а ) на множестве Ух достигается в некоторой точке х°, которой соответствуют значения /а-(а °) = f (рис. 9.8, о). Если х° является решением задачи НП, то f равны нулю и точка С = 0 оказывается точкой абсолютного максимума / (С) (рис. 9.8, б). [c.341]
| Рис. 9.8. Случай совпадения условного и безусловного максимумов (а) — линии уровня целевой функции и ограничения (б) — характер функции достижимости | 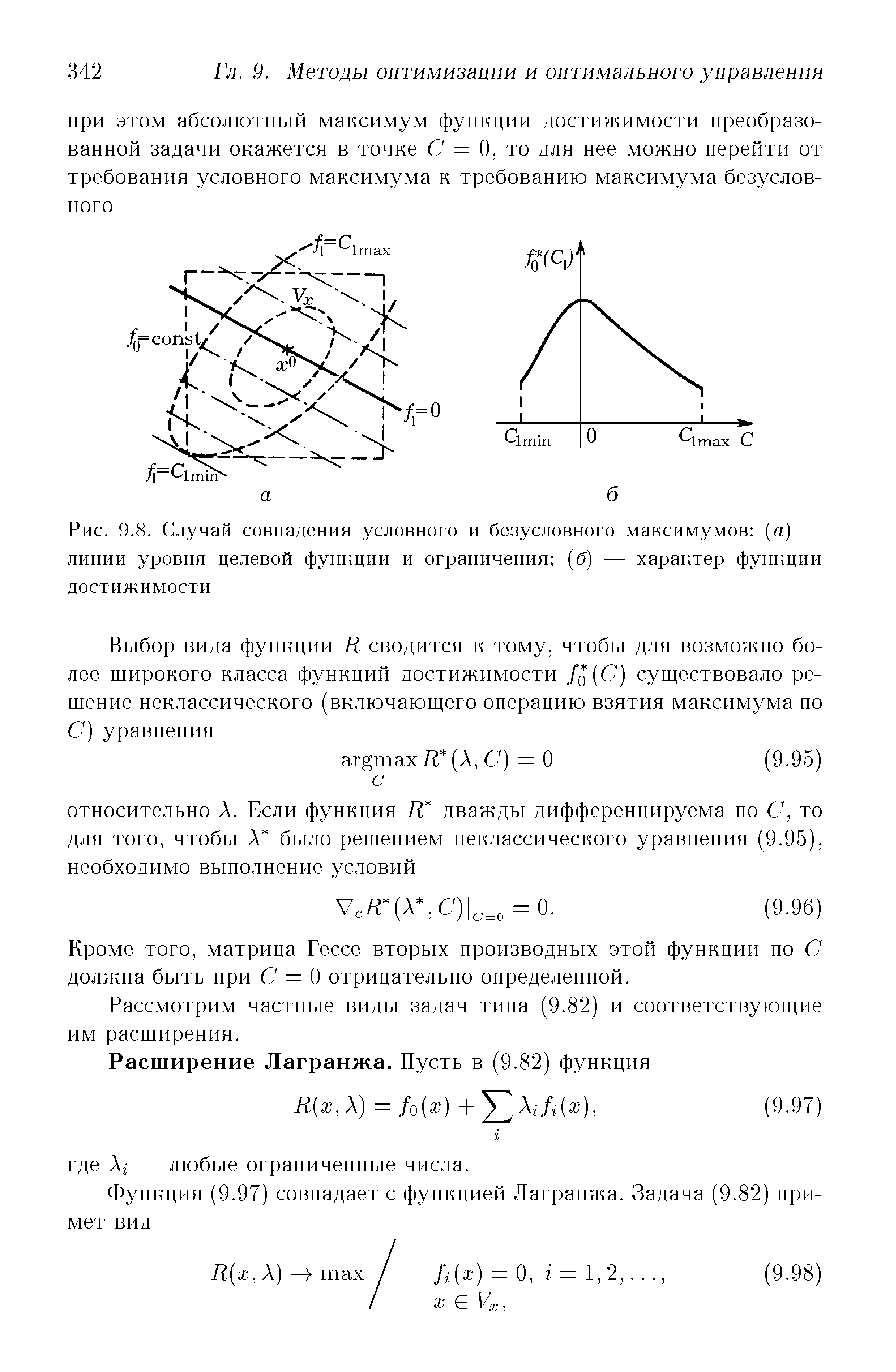 |
Процесс оптимизации (выработки оптимального решения) можно трактовать как поиск и выбор наилучшего с некоторой точки зрения варианта среди множества допустимых. Оптимизация представляет процесс нахождения экстремума (максимума или минимума) функции при заданных ограничениях (условная оптимизация) или без ограничений (безусловная оптимизация). [c.207]
Максимум в задаче безусловной оптимизации можно искать, например, применив сначала необходимое, а затем — достаточное условие существования экстремума. Согласно необходимому условию производная от функции по аргументу должна быть равна нулю. После несложных преобразований находим, что это условие выполняется для стационарной точки vl = 3,5. Достаточное условие для задачи на максимум состоит в отрицательности второй производной от функции по ее аргументу в стационарной точке. Это условие также выполняется. Следовательно, решением задачи (3.15), задающим компромиссное решение Нэша в биматричной игре с угрозами, будут значения v 3,5 v2= 1,5. Точка (ц,г>2) = (1,5 3,5) на эффективной границе области допустимых решений на рис. 3.7 отмечена кружком. [c.256]
На рис. 8.4 дана геометрическая иллюстрация решения задачи (5),(6). На линии L, по которой пересекаются вертикальная плоскость Q и график Гг функции (5), самой низкой точкой является точка />0=(х,° . 0,У))=(1/2,1/2,1/2). На поверхности У самой низкой является точка 0 = (0,0,0). Таким образом, на рис. 4 видно, что условный глобальный минимум функции (5), который равен глобального максимума и абсолютного глобального максимума. [c.124]
БЕЗУСЛОВНЫЙ МИНИМУМ, МАКСИМУМ ФУНКЦИИ [un onditional minimum, maximum] — минимум максимум) функции, не обусловленный ограничениями задачи. Ср. Условный минимум, условный максимум. [c.30]
Прежде всего заметим, что поставленная нами задача может не иметь решения. Для того чтобы понять это, достаточно рассмотреть такие хорошо знакомые функции, как U(x) = ах либо U(x) = ах3. Поэтому в дальнейшем при анализе задачи безусловной оптимизации будем предполагать, что существует пексг-торая точка х, на которой достигается решение задачи. Более того, для простоты исследования в дальнейшем будем полагать, что U(x )>U(x) для всех х х (как принято говорить, х является точкой строгого максимума). В классических задачах предполагается, что функция U(x) является достаточно гладкой, т. е. она имеет необходимое число производных. Тогда в окрестности точки х функцию U(x) можно разложить в ряд Тейлора [c.43]
Методы поиска оптимальной точки, рассмотренные в этом разделе, позволили решить многие задачи механики, а также наиболее простые экономические задачи. Необходимо, однако, заметить, что в случае достаточно сложных функций U(x) решение уравнений (4.11) и тем более (4.12) представляется крайне затруднительным. Поэтому даже для функций с единственным локальным максимумом проблему безусловной оптимизации нельзя считать решенной только на основе соотношений (4.11) и (4.12). Проблема еще более усложняется, если функция U(x) не является достаточно гладкой. f С появлением вычислительной техники широкое распространение получили так называемые градиентные методы, состоящие в определении направления наискорейшего роста функции U(x) и в переходе от некоторой исходной точки к другой, более предпочтительной. Затем новая точка берется за исходную и процесс повторяется. В настоящее время построены различные варианты градиентных методов и разработаны вычислительные системы, позволившие численно решить многие важные задачи безусловной оптимизации (см., например, [31]). Однако проблему многоэкстремальности (т. е. неединственности локального экстремума) до сих пор нельзя считать решенной. [c.45]
ОПТИМАЛЬНАЯ (ИЛИ ОПТИМИЗАЦИОННАЯ) ЗАДАЧА [optimization problem] — экономико-математическая задача, цель которой состоит в нахождении наилучшего (с точки зрения какого-то критерия) распределения наличныхресурсов. (Иногда то же Экстремальная задача.) Решается с помощью оптимальной модели методами математического программирования, т.е. путем поиска максимума или минимума некоторых функций или функционалов при заданных ограничениях (условная оптимизация) и без ограничений (безусловная оптимизация). [c.242]
