Рассмотренные методы решения одномерной задачи безусловной оптимизации могут быть распространены и на многомерный случай. Пусть теперь х е Еп. Тогда условие (4.9) заменяется условием [c.45]
Задачи безусловной оптимизации, которым мы уделили внимание в этом разделе, довольно редко встречаются в экономических исследованиях, основной особенностью которых является ограниченность используемых ресурсов. Достоинством задачи безусловной оптимизации является то, что к ней (или к поиску ста- [c.45]
Безусловная оптимизация начинается с первого шага. [c.278]
Процесс оптимизации (выработки оптимального решения) можно трактовать как поиск и выбор наилучшего с некоторой точки зрения варианта среди множества допустимых. Оптимизация представляет процесс нахождения экстремума (максимума или минимума) функции при заданных ограничениях (условная оптимизация) или без ограничений (безусловная оптимизация). [c.207]
Логическая схема методов решения задачи НП, связанных с переходом к безусловной оптимизации, в общих чертах такова. [c.337]
| Рис. 1. Безусловная оптимизация функции одного аргумента | 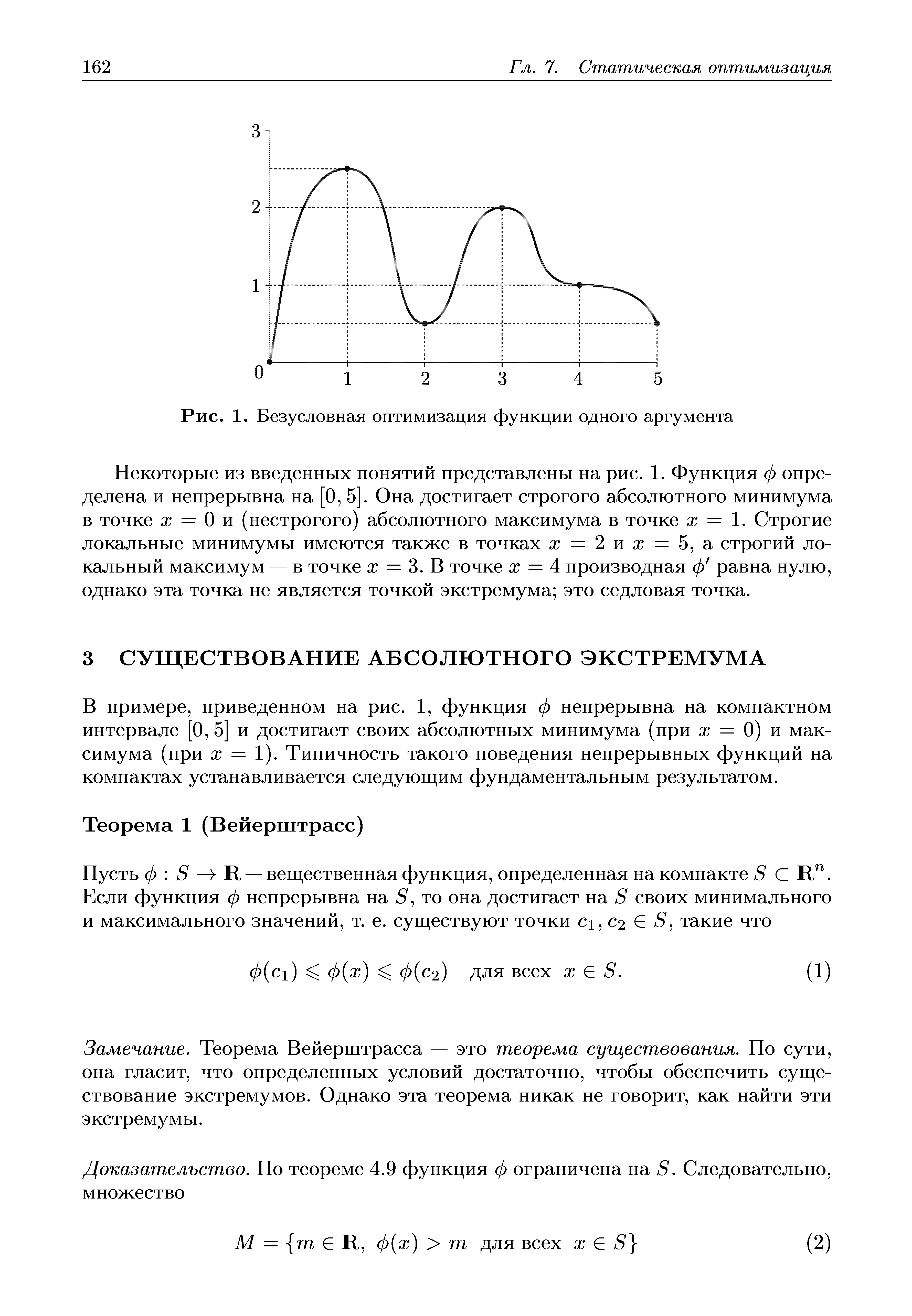 |
Стремление свести задачу на условный экстремум к задаче безусловной оптимизации всегда было одной из ведущих тенденций теории экстремальных задач. Это сведение осуществляется фундаментальной теоремой Куна—Танкера. Задача [c.461]
Используется какой-нибудь алгоритм безусловной оптимизации, например, метод градиента, усиленный привлечением идей метода сопряженных градиентов. Точка и используется, как начальная в этом процессе спуска. После этого в новой точке и, g, л делается пересчет множителей Лагранжа [c.462]
Алгоритм безусловной оптимизации 393 [c.484]
Методы спуска (общая схема) [3]. Все методы спуска решения задачи безусловной оптимизации (8.17) различаются либо выбором направления спуска, либо [c.176]
Методы спуска (8.1.) — методы решения задач безусловной оптимизации, связанные с выбором направления спуска и способов движения вдоль направления спуска. [c.345]
Максимум в задаче безусловной оптимизации можно искать, например, применив сначала необходимое, а затем — достаточное условие существования экстремума. Согласно необходимому условию производная от функции по аргументу должна быть равна нулю. После несложных преобразований находим, что это условие выполняется для стационарной точки vl = 3,5. Достаточное условие для задачи на максимум состоит в отрицательности второй производной от функции по ее аргументу в стационарной точке. Это условие также выполняется. Следовательно, решением задачи (3.15), задающим компромиссное решение Нэша в биматричной игре с угрозами, будут значения v 3,5 v2= 1,5. Точка (ц,г>2) = (1,5 3,5) на эффективной границе области допустимых решений на рис. 3.7 отмечена кружком. [c.256]
Градиентные методы решения задач безусловной оптимизации. Ведущее место среди прямых методов решения экстремальных задач занимает градиентный метод (точнее, семейство градиентных методов) поиска стационарных точек дифференцируемой функции. Напомним, что стационарной называется точка, в которой V/(jt) = 0 и которая в соответствии с необходимым условием оптимальности является подозрительной на наличие локального экстремума. Таким образом, применяя градиентный метод, находят множество то- [c.86]
Оптимизационные задачи для выпуклых функций. Общим недостатком рассмотренных выше методов безусловной оптимизации было, с одной стороны, то, что они позволяют отыскивать только точки, подозрительные на локальный экстремум, а с другой — то, что найденные решения могут существенно зависеть от начального приближения. Поиск глобального оптимума подразумевает перебор найденных точек, который, [c.89]
Условная и безусловная оптимизация. [c.107]
С учетом ограничения участия (которое в точке решения выполняется как равенство) ее можно свести к следующей задаче безусловной оптимизации по уровню усилий х [c.575]
Сначала мы найдем решение соответствующей задачи безусловной оптимизации (не учитывая ограничения xl > х2), а затем покажем, что это ограничение выполняется в полученном решении, и поэтому несущественно. [c.603]
В заключение раздела приведем (без подробного анализа вычислительных свойств) две другие функции оценки, предназначенные для сведения нелинейной задачи о дополнительности N P(F) к обычной задаче безусловной оптимизации типа тшМ(ж). [c.62]
Проведем безусловную оптимизацию. , Ее результаты отмечены в таблице. [c.491]
Говоря об оптимизации СПО, не следует понимать под этим только их ускорение. Оптимизация спуско-подъемных операций — это в первую очередь технологическая дисциплина, качественная эксплуатация бурового оборудования, безусловное выполнение требований охраны труда. [c.208]
Расчеты, проведенные по ряду нефтеперерабатывающих заводов Башкортостана, показали высокую экономическую эффективность оптимизации производственной программы. Выбор оптимальной производственной программы дает возможность до 20-25% увеличить прибыль предприятия. Это, безусловно, положительно скажется на общем финансовом положении предприятия. [c.117]
Учет затрат по процессам с объединением их в центрах финансовой ответственности Закупка , Производство , Сбыт , Управление наилучшим образом подходит для организации управленческого учета. Таким образом построенный управленческий учет дает возможность применить к оптимизации результатов деятельности предприятия системный подход, что, безусловно, ведет к повышению эффективности функционирования предприятия. [c.280]
Безусловно, сделанные выводы по результатам решения задачи по оптимизации использования бутиленов носят ориентировочный характер. Исследования в этом направлении, очевидно,. должны быть продолжены, ибо рациональное направление использования не только ресурсов бутилена, но и в целом-всех видов углеводородного сырья способствует не только экономии живого и овеществленного труда, но и степени наиболее эффективного использования такого невосполнимого природой источника сырья, как нефть. [c.155]
В предыдущей главе были обособлены четыре основных субъекта финансовых отношений безусловно, ключевую роль играют два из них — государство и предпринимательский сектор. Поэтому систему управления финансами в целом, имеющую целью оптимизацию денежных потоков, целесообразно рассматривать как двухуровневую модель [c.43]
Оборачиваемость запасов (в оборотах). Как уже отмечалось, важнейшие индикаторы финансово-хозяйственной деятельности — выручка от продаж и прибыль — находятся в прямой зависимости от показателей оборачиваемости. Взаимосвязь здесь очевидна — предприятие, имеющее относительно небольшой запас оборотных средств, но более эффективно их использующее, может добиться тех же результатов, что и предприятие с большим объемом оборотных активов, но нерациональной их структурой и завышенной по сравнению с текущими потребностями величиной. Кроме того, оборотные активы, находящиеся на разных стадиях кругооборота, как правило, взаимосвязаны поэтому, ускорение оборачиваемости на отдельной стадии чаще всего сопровождается мерами по ускорению оборачиваемости и на других стадиях. Политика оптимизации управления запасами, будучи принятой на предприятии, безусловно не может быть выборочной (например, контролируем оборачиваемость запасов, но [c.353]
Создание АИС способствует повышению эффективности производства экономического объекта и обеспечивает качество управления. Наибольшая эффективность АИС достигается при оптимизации планов работы предприятий, фирм и отраслей, быстрой выработке оперативных решений, четком маневрировании материальными и финансовыми ресурсами и т.д. Поэтому процесс управления в условиях функционирования автоматизированных информационных систем основывается на экономико-организационных моделях, более или менее адекватно отражающих характерные структурно-динамические свойства объекта. Адекватность модели означает прежде всего ее соответствие объекту в смысле идентичности поведения в условиях, имитирующих реальную ситуацию, поведение моделируемого объекта в части существенных для поставленной задачи характеристик и свойств. Безусловно, полного повторения объекта в модели быть не может, однако несущественными для анализа и принятия управленческих решений деталями можно пренебречь. Модели имеют собственную классификацию, подразделяясь на вероятностные и детерминированные, функциональные и структурные. Эти особенности модели порождают разнообразие типов информационных систем. [c.18]
Если предположить, что существует rD — ограничение сверху на ставку депозитов, то задача поиска безусловного максимума функции T[(rD,rL) трансформируется в задачу условной оптимизации с одним связующим ограничением [c.110]
В задачах условной оптимизации критической точкой называется критическая точка функции ф(х), определенной на поверхности g(x) = О, а не критическая точка функции ф(х), координаты которой удовлетворяют соотношениям g(x) = 0 (хотя, безусловно, все такие точки будут критическими в выше определенном смысле, но не наоборот). [c.180]
Прежде всего заметим, что поставленная нами задача может не иметь решения. Для того чтобы понять это, достаточно рассмотреть такие хорошо знакомые функции, как U(x) = ах либо U(x) = ах3. Поэтому в дальнейшем при анализе задачи безусловной оптимизации будем предполагать, что существует пексг-торая точка х, на которой достигается решение задачи. Более того, для простоты исследования в дальнейшем будем полагать, что U(x )>U(x) для всех х х (как принято говорить, х является точкой строгого максимума). В классических задачах предполагается, что функция U(x) является достаточно гладкой, т. е. она имеет необходимое число производных. Тогда в окрестности точки х функцию U(x) можно разложить в ряд Тейлора [c.43]
Методы поиска оптимальной точки, рассмотренные в этом разделе, позволили решить многие задачи механики, а также наиболее простые экономические задачи. Необходимо, однако, заметить, что в случае достаточно сложных функций U(x) решение уравнений (4.11) и тем более (4.12) представляется крайне затруднительным. Поэтому даже для функций с единственным локальным максимумом проблему безусловной оптимизации нельзя считать решенной только на основе соотношений (4.11) и (4.12). Проблема еще более усложняется, если функция U(x) не является достаточно гладкой. f С появлением вычислительной техники широкое распространение получили так называемые градиентные методы, состоящие в определении направления наискорейшего роста функции U(x) и в переходе от некоторой исходной точки к другой, более предпочтительной. Затем новая точка берется за исходную и процесс повторяется. В настоящее время построены различные варианты градиентных методов и разработаны вычислительные системы, позволившие численно решить многие важные задачи безусловной оптимизации (см., например, [31]). Однако проблему многоэкстремальности (т. е. неединственности локального экстремума) до сих пор нельзя считать решенной. [c.45]
ОПТИМАЛЬНАЯ (ИЛИ ОПТИМИЗАЦИОННАЯ) ЗАДАЧА [optimization problem] — экономико-математическая задача, цель которой состоит в нахождении наилучшего (с точки зрения какого-то критерия) распределения наличныхресурсов. (Иногда то же Экстремальная задача.) Решается с помощью оптимальной модели методами математического программирования, т.е. путем поиска максимума или минимума некоторых функций или функционалов при заданных ограничениях (условная оптимизация) и без ограничений (безусловная оптимизация). [c.242]
Условие (7.109) позволяет выразить с и с2 через п. Подставляя эти зависимости в (7.108), получим задачу безусловной оптимизации по п. Найдя ее решение п, вычислим с[,с 2] они определяют разбиение подсистем на продацов и покупателей . Конкретезируем зависимости n как [c.270]
Правда, расчет предотвращенного ущерба по Временной типовой методике /1/, как правило, дает результаты, намного превышающие затраты, что заведомо их оправдывает практически в каждом случае. В большой мере это происходит из-за учета внеэкономической составляющей в расчетных формулах (например из-за учета скорости оседания частиц и радиуса их рассеивания), что завышает размер предотвращенного ущерба подобно тому, как это происходит при переводе задачи оптимизации с ограничениями в задачу безусловной оптимизации. Однако при этом предотвращенный ущерб теряет свое экономическое содержание, а следовательно, сопоставление его с затратами не будет иметь смысла. Например, затраты, направленные на снижение загрязнения какого-либо уникального природного ландшафта (заповедника) вряд ли смогут быть оправданы реальным предотвращенным ущербом, поскольку природные компоненты этого ландшафта не имеют адекватной стоимостной оценки. Стремление сохранить уникальный объект природы, продиктованное отнюдь не экономическими соображениями, заставляет для оправдания затрат завышать реальный размер предотвра- [c.124]
Левитин Е.С. Об оценках устойчивости по решению в задаче безусловной оптимизации. - Ж. вычисл- матем. и матем. физ., 1976, № 3, с. 585 - 596. [c.437]
Так, если маркетинг осуществляется в пределах одной страны, то его, безусловно, можно назвать национальным, а если за границей — международным либо экспортным, либо импортным [30, с. 14]. Наличие первого признается многими специалистами, но со вторым — не все так однозначно. Импортный маркетинг связан с применением особой технологии продвижения продуктов на рынок, оптимизацией процесса продаж и т. п. Мы разделяем позицию тех, кто в импортном маркетинге видит особую форму исследования рынка для обеспечения высокоэффективных закупок. К библиотекам это понятие применимо, так как они вынуждены изучать некоторые профильные рынки за границей, например, внешний книжный рынок ( с образованием СНГ данное направление работы усиливается). Синонимами международного маркетинга являются понятия мультинациональный, внешнеэкономический, внешнеторговый. Национальные и паранацио-нальные, а также многие региональные, отраслевые и территориальные библиотечно-информационные центры России активно развивают зарубежные деловые контакты, и в русле этой деятельности можно успешно реализовать принципы международного маркетинга. [c.66]
Вместе с тем невыпуклость / (С) часто не препятствует использованию квадратичного штрафа. Пусть, например, / (С) = 1 + С2 (рис. 9.13, б), функция вогнута и использование расширения Лагран-жа не позволяет свести задачу условной оптимизации к безусловной. Функция достижимости в задаче с использованием квадратичного штрафа имеет вид [c.353]
Важнейшими задачами внутриструктурного планирования являются также выполнение комплекса нормативно-плановых расчетов и оптимизация принимаемых решений по всем вышеперечисленным целям, а также опережающее воздействие на исполнителей, ресурсы, сроки, а иногда и программу действий, обеспечивающих безусловное достижение конечных реаультатов научной организации. В процессе планирования составляется рациональный план работы. План—это заранее определенное направление действий. Он включает 1) ориентацию на будущее 2) действие 3) элемент, определяющий лицо или организацию-исполнителя 4) сроки. [c.190]
